等温压缩空气储能系统喷水量研究
何子伟, 罗马吉, 涂正凯
(1.武汉理工大学现代汽车零部件技术湖北省重点实验室, 430070, 武汉; 2.武汉理工大学汽车零部件技术湖北省协同创新中心, 430070, 武汉; 3.武汉理工大学材料复合新技术国家重点实验室, 430070, 武汉)
等温压缩空气储能系统喷水量研究
何子伟1,2, 罗马吉1,2, 涂正凯3
(1.武汉理工大学现代汽车零部件技术湖北省重点实验室, 430070, 武汉; 2.武汉理工大学汽车零部件技术湖北省协同创新中心, 430070, 武汉; 3.武汉理工大学材料复合新技术国家重点实验室, 430070, 武汉)
为了揭示等温压缩空气储能系统中不同参数对喷水量的影响,提出了利用多变指数接近1的多变压缩来研究近等温压缩,将压缩终态的气态水、液态水、空气视为理想混合物,分析了压缩能量的分布状况,并运用饱和水蒸气分压公式、道尔顿分压定律和组分热力学参数,研究了不同状态参数下所需喷水量。研究表明,适当增大压比或降低终温(喷水量增大)可使得传热量比例增大,当压比为10、转速为100 r/min时,喷水量由5.73 kg/s提高至8.68 kg/s,传热量比例提高了5%;压比、传热效率、终温均对空气与水质量之比有影响;其他条件一定时,转速对空气与水质量之比没有影响,当压比为10,传热效率为95%,终温为50 ℃,转速分别为60、100、150 r/min时,空气与水质量之比均为0.86;较低压强(压比小于10)不利水储热的进行。
压缩空气储能;等温压缩;储热;饱和水蒸气分压
近年来,电力的生产量和消耗量在世界范围内呈持续增长状态,越来越多的国家都采取了鼓励可再生能源(风能、太阳能等)的政策和措施,可再生能源发电发展迅猛。但是,由于缺乏配套的大规模电力储能系统,使得当前“弃风”“弃光”现象严重,导致可再生能源利用率长期处于低水平。中国作为世界上能源大国之一,新能源发电增长迅速,截至2015年底,我国风电、太阳能发电累计装机容量达到170 GW,位居世界第一[1],但“弃风”问题非常严峻。数据显示,2011—2015年中国弃风电量累计损失达到959亿kW/h,全国5年的平均弃风率为13.4%,电费损失累计约518亿元[2]。大规模电力储能系统的发展将有效提高可再生能源发电高利用率,并能实现电网的“削峰填谷”。
压缩空气储能(CAES)作为最具发展潜力的储能方式拥有诸多优势,如储能级别高、转换效率高、无地理因素限制(储气罐替代储气洞穴的CAES)、无资源约束(工作介质为空气)等。目前,国外已有两座运营的压缩空气储能电站,分别为德国Huntorf电站(1978,321 MW,642 MW/h,η=42%)和美国McIntosh电站(1991,110 MW,2 860 MW/h,η=54%);其他的示范项目包括欧洲的Adele(90 MW)和美国的Sustain X(1.5 MW)项目都在建设中。国内的压缩空气储能研究主要包括中科院工程热物理研究所建设的先进压缩空气储能示范系统(10 MW)和清华大学建设的TICC-500(0.5 MW)[3-6]。
等温压缩空气储能(I(isothermal)-CAES)作为CAES中转换效率最高的储能类型,目前处于研究和示范过程中。早期,Coney等人开发了一种新型的等温压缩机,并进行了理论和样机实验验证,其中等温压缩是通过改装后的船用柴油机气缸内部的喷嘴喷射大量的水来实现,在压缩机转速达到380 r/min时,压缩空气的温度始终保持在100 ℃以下[7]。Ven等人提出了液体活塞概念,液体活塞中的液体柱位于活塞以上的气体压缩室,研究表明通过增加水的比表面积(面积/体积)增加了传热效率,这使得压缩空气的温度大大降低,压缩功降低,压缩效率提升[8]。Qin等人将喷射水雾和液体活塞相结合,仿真在低转速60 r/min下进行,并考虑了液滴尺寸、液滴总注入量和喷射方法(预混喷射和直接喷射)的影响,研究表明减小液滴尺寸使得传热有更大的总表面积,液滴最优尺寸20 μm更接近于等温效果且直接喷射水雾效果更好[9]。LightSail Energy公司运用喷射水雾方法来实现等温压缩[10],Sustain X公司运用预混合水泡沫来实现等温压缩[11],二者都是通过增大传热介质的比表面积来实现等温压缩。目前有关等温压缩空气储能的研究都集中在不同实现方法理论和模型验证,本文提出了利用多变指数接近1的多变压缩来研究近等温压缩,分析了等温压缩(喷射水方式)压缩过程中的能量分布规律,研究了不同参数对压缩过程中空气与水的质量比的影响,计算结果可以为实验研究提供参考。
1 等温压缩空气储能
1.1 压缩空气储能原理与分类
CAES系统作为一种可实现大容量和长时间电能储存的电力储能系统,一般包括压气机、燃烧室及换热器、透平、储气装置(地下洞穴或压力容器)、电动机/发电机5个主要部件[12-13]。其通过压缩空气储存多余的电能(电网负荷低谷期),在需要时将高压空气释放,通过膨胀机做功发电(电网负荷高峰期),从而完成储能和释能过程,具有聚纳新能源和削峰填谷等功能[14]。压缩空气储能按能量来源可以分为补燃式和非补燃式两类[1]。根据热量在空气压缩期间和膨胀之前的处理过程,压缩空气储能在技术层面分为非绝热、绝热和等温,储能类型分为非绝热压缩空气储能(D(diabatic)-CAES)、绝热压缩空气储能(A(adiabatic)-CAES)和等温压缩空气储能(I(isothermal)-CAES)[3]。D-CAES需要借助燃料(天然气等)补燃来实现系统运行属于补燃式,A-CAES和I-CAES由于利用系统本身的压缩热来实现系统循环运行属于非补燃式。非补燃式CAES提高了系统效率和储能级别,并且清洁环保无污染,可利用大容量、高可靠性压力容器储气克服了储气洞穴的地理条件限制。
1.2 等温压缩空气储能原理
与传统的补燃式压缩空气储能结构不同的是,I-CAES将压气机和透平功能在一个活塞机构中实现,带来了充分的热交换时间和慢压缩(膨胀)过程,其结构原理图如图1所示。充电储能过程:在电网负荷低峰期,电网输入电能,电机驱动活塞机构压缩空气实现压气机的功能,通过在压缩期间喷射水雾(预混合水泡沫)或利用液体活塞进行大面积的热交换以实现等温压缩[3],这部分热量储存在水或水泡沫中,高压空气被分离储存在储气罐中。放电释能过程:在电网负荷高峰期,高压空气和高压水进入活塞机构膨胀,活塞机构驱动发电机进行发电并入电网。在等温压缩空气储能系统中,由于气体温升较低,在压缩期间消耗的压缩功少,在膨胀期间提供几乎相同的压缩热在恒温下膨胀,整个过程压缩热被充分利用,因此等温压缩空气储能的理想效率高[3]。

图1 I-CAES系统结构原理图
2 热力学分析
2.1 等温压缩与绝热压缩
压缩过程有绝热压缩(不发生任何传热)和等温压缩(最大理想传热)两种极限情况,p-V图分别如图2中的1-2s和1-2T所示,而实际压缩过程往往为多变压缩过程,即图中的1-2n。
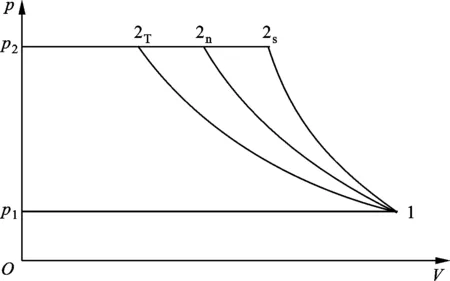
图2 不同压缩过程的p-V图
压缩气体的生产过程包括气体的流入、压缩和输出,所以压气机耗功应以技术功计。由图2可知,W2s>W2n>W2T,说明绝热压缩所消耗的功最多,等温压缩最少,多变压缩介于两者之间,并且随着多变指数的减小而减小[15]。此外由于绝热压缩后温升较高,对组件的耐热性要求较高,且压缩后的空气所占体积大,系统储能密度低。因此,应减小多变指数,使压缩过程接近于等温过程,这样不仅有利于提高系统储能级别和效率,还可降低组件的耐热性要求。由以上分析可以得出,等温压缩空气储能在诸多方面性能优于绝热压缩空气储能。
2.2 近等温压缩的多变指数
在实现等温压缩空气的过程中,由于储热介质不会将压缩热全部吸收且空气本身具有压力提高的内能,因此空气的初温和终温不可能一致。目前研究的等温压缩终温一般小于80 ℃[16],相比于温差很大的绝热压缩,该过程被称为近等温压缩过程。其多变指数由式(1)求得
(1)
(2)
式中:n为多变指数;T2为终态温度;T1为初态温度;p2为终态压强;p1为始态压强;CR为压比。假设压缩空气为理想气体,它和水的初始温度和终态温度一致,取初始温度为20 ℃,终态温度分别为50、60、70 ℃,取始态压强为大气压0.1 MPa,压缩过程分为多级压缩,选择计算对象作为第一级压缩,压比分别为2、5、10、15、20。经过计算得出终态温度、压比与多变指数的关系如图3所示。

图3 不同状态参数下多变指数图
如图3所示,当压比一定时,随着终温的降低,压缩过程中温差减小,多变指数逐渐减小且趋近于1,压缩过程越接近等温过程,因此利用多变指数接近1的多变压缩过程来研究近等温压缩过程。此外,当温差一定时,随着压比的提升,多变指数也在减小,说明适当提高储气压力有利于近等温压缩过程的实现。
3 能量和喷水量计算
3.1 能量计算
由于压缩过程会产生大量的压缩热,喷射进气缸内的部分水会由液态水转变为气态水,此时压缩终态的混合物由空气、液态水、气态水所组成,压缩功的能量转变为空气内能、气态水储热能、液态水储热能、流动功等能量。
压缩功
(3)
式中:Rg为理想空气气体常数。
过程热量
(4)

cv=c0-Rg+c1θ+c2θ2+c3θ3
(5)
式中:c0=1.05;c1=-0.365;c2=0.85;c3=-0.39;θ=T/1 000[17]。
对于较小的温差,在平均温度下c可以被当做常数使用[18],因此每一个终态温度对应一个平均比定容热容,产生qn这部分能量通过热传递使得部分液态水由液态变为气态,热能被储存在气态水和剩余的液态水中。
空气储能(内能变化量)
u2-u1=Δu=Δh-Δ(pv)=
(6)
Δh=qn-wt
(7)
式中:u2为压缩空气终态内能;u1为压缩空气始态内能;Δh为压缩过程中焓变,这部分能量由压缩空气内能变化量Δu和过程中的流动功Δ(pv)组成。
水储热
qw=qnη
(8)
式中:qw为储存在水(气态水和液态水)中的热能;η为传热效率,其值为实际传热量qw与理论上的最大传热量qn之比。损失的传热量包括压损和通过气缸壁传热耗散到环境中的能量,由于不同的等温压缩实现方式、喷射方式、水雾液滴的大小和质量等参数都会改变液体的比表面积,从而影响传热效率[7-11],因此取传热效率分别为85%、90%、95%、100%,以研究不同传热效率对喷水量的影响。
3.2 喷水量计算
假设压缩终态为理想状态:水转化为湿饱和蒸汽,气态水吸收热量达到饱和转化为饱和水蒸气,剩余液态水吸收热量转化为饱和水,此时热量被合理地分配在气态水和液态水中。为了得到不同参数与压缩过程中喷水量的关系,首先需确定多变过程的始态和终态参数,然后利用空气和水的热力学参数以及相关公式计算压缩过程中的气态水质量、液态水储热量、气态水储热量等,最终得到某一温度和压强下所需的喷水量。
空气质量流量
(9)
(10)
式中:d为缸径;L为活塞行程;V为压缩空气体积;N为曲轴转速。不考虑余隙容积。
水质量流量的求解过程如下。
不同温度下饱和水蒸气的压力为
lg(ps/101 325)=-2.179 4+
2.953×10-2(T2-273.15)-
9.183 7×10-5(T2-273.15)2+
1.445 4×10-7(T2-273.15)3
(11)
p2=pt=ps+pa
(12)
式中:ps为饱和水蒸气分压,由文献[19]中的数据拟合得到;pa为压缩空气分压。
道尔顿分压定律
(13)

根据式(13)得到空气和水蒸气的质量流量比为
(14)

在压缩过程中,湿蒸汽的干度
(15)
因此水储热
(16)
式中:hs为饱和水焓值;hH2O(g)为饱和水蒸气焓值;hH2O(in)为初始液态水焓值。
3种焓值根据终态参数结合IAPWS—IF97水和水蒸气热力学性质的国际工业公式计算得到[15],进而求得不同终态参数下的水质量,表1为计算过程中不同参数数值。

表1 计算参数
3.3 图像分析
由上述分析可知,压缩功的能量转化为空气内能、气态水储热能、液态水储热能、流动功等能量,图4为固定参数下压缩功能量转化的分布图。过程热量与压缩功的比值表示压缩功转化为水储热的能量比重,通过计算得到较优比值所需求的参数,图5为过程热量与压缩功比值随压比和终温变化的情况。通过计算不同参数下空气储能和水储热分布规律,使尽可能多的能量储存在水中,减少能量耗散,图6为空气储能与水储能比值随压比和终温变化的情况。

图4 压缩功能量转化分布图

图5 过程热量与压缩功比值随不同参数的变化曲线

图6 空气储能与水储能比值随不同参数的变化曲线
如图4所示,水储热占比最大,为了使这部分能量比例增加,对过程热量与压缩功比值随压比和终温的变化规律进行了研究,如图5所示。由图中可以看出,随着压比的增大或终温的降低,比值逐渐增大并趋于恒定达到极值。当压比为10、转速为100 r/min、终温分别为60 ℃(喷水量为5.73 kg/s)和50 ℃(喷水量为8.68 kg/s)时,比值分别达到80%和85%;对于终温为70 ℃(喷水量为3.78 kg/s)的状态,比值要达到80%,则需要把压比提高到20,说明在等温压缩的实现过程中,应该适当增大压比或者降低终温(提高喷水量)使得传热量比例增大,从而增大储存在水中的热量比例。
由图4还可看出,空气储能与水储热比值接近1/5,为使这一比值降低,对空气储能与水储热比值随压比和终温的变化规律进行了研究,如图6所示。由图中可以看出,随着压比的增大或终温的降低,空气储能与水储热比值逐渐降低并趋于恒定。当终温为60 ℃时,随着压比的增大,比值由1.5降低到1/10左右,更多的能量被储存在水中(热损减小);当压比大于10之后,比值只有较小的改变,因此再增大压比对于增大该比例无明显意义,但可以增大传热量。由图6还可得出,压强较低(压比小于10)时不利于水储热的进行。
为了得出不同参数对压缩过程中空气与水的质量比的影响规律,计算并分析了不同参数下所需喷水量,得出压缩空气量与喷水量比值。图7表示空气与水质量随不同参数变化的情况。
由图7a可知:由于气缸缸径和行程固定,所以压缩空气的质量与曲轴转速成正比关系且保持恒定;当转速一定时,随着混合物终温的降低,所需喷水量增大。这是因为压缩过程中产生的热量迅速将压缩空气的温度提升,而水的热容比空气大,喷水量的增多使得水中储存更多的热量,压缩空气的温升降低,最终形成温度相同的空气、饱和水、饱和水蒸气组成的理想混合物。对于3种不同的转速,在压比、终温、传热效率一定时,压缩空气量与喷水量之比相同:压比为10,传热效率为95%,终温为50 ℃,转速分别为60、100、150 r/min时,空气与水质量比均为0.86。

(a)不同转速(CR=10,η=95%)
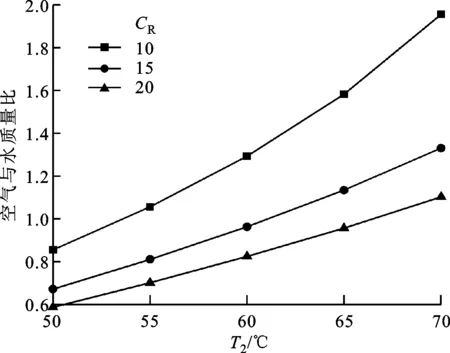
(b)不同压比(N=100 r/min,η=95%)

(c)不同传热效率(CR=10)图7 不同参数下空气与水质量比
由图7b可知:压比一定时,随着混合物终温的升高,空气与水质量比呈线性增长,所需喷水量减少;当终温一定时,随着压比的增大,空气与水质量比降低,所需喷水量增大。这是由于终态压强的增大,饱和水蒸气分压不变,气态水质量变少,储存在气态水中的热量减少,而传热量随压比增大升高,储存在液态水中的热量升高,因此所需喷水量增大。
由图7c可知:传热效率一定时,随着混合物终温的升高,空气与水质量比呈线性增长,所需喷水量减少;当终温一定时,随着传热效率的增大,空气与水质量比降低,所需喷水量增大。这是因为传热效率增大,储存在水中的总热量增大,而储存在气态水中的热量一定,因此所需的液态水量提高。
4 结论与展望
本文通过热力学公式和物质的热力学参数计算并分析了理想状态下等温压缩空气储能的能量分布,利用饱和水蒸气压和道尔顿分压定律求解不同参数下空气与水质量比,并得出以下结论。
(1)多变指数逐渐减小且趋近于1,压缩过程越接近等温过程,温差不变,随着压比的提升,多变指数也在减小,说明适当的提高储气压力有利于近等温压缩过程的实现。
(2)由压缩功能量转化分布图和能量比值变化图可以得出,在等温压缩的实现过程中,应该适当增大压比或降低终温使得传热量比例和水储热比例增大。当压比为10时,喷水量由5.73 kg/s提高至8.68 kg/s,传热量比例提高了5%;较低压强(CR<10)不利水储热的进行。
(3)对于第一级压缩,可以将压比确定为10,此时传热量和水储热比例都达到良好状态。由于水的热容比空气大,压比一定时,增大喷水量降低了压缩空气的温升,可以使终温达到50 ℃,甚至更低,压缩过程更接近等温过程。
(4)每一个终温、压比、传热效率和转速对应一个固定的喷水量,可以为实验研究提供理论数据并对比。压比、传热效率、终温均对空气与水质量比有影响;其他条件一定时,转速对空气与水质量比没有影响,当压比为10,传热效率为95%,终温为50 ℃,转速分别为60、100、150 r/min时,空气与水质量比均为0.86。
本文的相关计算是基于假设:空气为理想气体、压缩过程均为可逆和压缩终态为理想状态混合物,后期可以进行实际情况的理论计算并通过实验进行对比。对于传热效率是根据相关文献自拟的数据,由于不同的喷射方式以及水雾液滴的大小和质量等参数都会影响传热效率,后期可以针对传热效率建立传热模型进行相关分析。相关文献计算了等温压缩空气储能系统效率,储能效率作为该系统重要参数不可忽视,后期可以计算不同参数(终温、压比、传热效率)下整个系统的储能效率。
[1] 梅生伟, 薛小代, 陈来军. 压缩空气储能技术及其应用探讨 [J]. 南方电网技术, 2016, 10(3): 11-15.
MEI Shengwei, XUE Xiaodai, CHEN Laijun. Discussion on compressed air energy storage technology and its application [J]. Southern Power System Technology, 2016, 10(3): 11-15.
[2] 张玥. 2011年—2015年中国弃风数据统计 [J]. 风能, 2016(2): 34-35.
ZHANG Yue. China abandoned wind data statistics from 2011 to 2015 [J]. Wind Energy, 2016(2): 34-35.
[3] BUDT M, WOLF D, SPAN R, et al. A review on compressed air energy storage: basic principles, past milestones and recent developments [J]. Applied Energy, 2016, 170: 250-268.
[4] VENKATARAMANI G, PARANKUSAM P, RAMALINGAM V, et al. A review on compressed air energy storage: a pathway for smart grid and polygeneration [J]. Renewable and Sustainable Energy Reviews, 2016, 62: 895-907.
[5] IBRAHIM H, ILINCA A, PERRON J. Energy storage systems: characteristics and comparisons [J]. Renewable and Sustainable Energy Reviews, 2008, 12(5): 1221-1250.
[6] CHEN L J, ZHENG T W, MEI S W, et al. Review and prospect of compressed air energy storage system [J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 529-541.
[7] CONEY M W, STEPHENSON P, MALMGREN A, et al. Development of a reciprocating compressor using water injection to achieve quasi-isothermal compression [C]∥Proceedings of the 16th International Compressor Engineering Conference. West Lafayette, USA: Purdue University Purdue e-Pubs, 2002: 1508.
[8] VAN DE VEN J, LI P. Liquid piston gas compression [J]. Applied Energy, 2009, 86(10): 2183-2191.
[9] QIN C, LOTH E. Liquid piston compression efficiency with droplet heat transfer [J]. Applied Energy, 2014, 114: 539-550.
[10] CRANE S E, BERLIN E P, Jr, ABKENAR A H P, et al. Compressed air energy storage system utilizing two-phase flow to facilitate heat exchange: US8215105 B2 [P]. 2012-07-10.
[11] MCBRIDE T O, BOLLINGER B, BESSETTE J, et al. Systems and methods for foam-based heat exchange during energy storage and recovery using compressed gas: US20130074485 A1 [P]. 2013-03-28.
[12] 张新敬, 陈海生, 刘金超, 等. 压缩空气储能技术研究进展 [J]. 储能科学与技术, 2012(1): 26-40.
ZHANG Xinjing, CHEN Haisheng, LIU Jinchao, et al. Research progress in compressed air energy storage system: a review [J]. Energy Storage Science Technology, 2012(1): 26-40.
[13] 陈海生, 刘金超, 郭欢, 等. 压缩空气储能技术原理 [J]. 储能科学与技术, 2013(2): 146-151.
CHEN Haisheng, LIU Jinchao, GUO Huan, et al. Technical principle of compressed air energy storage system [J]. Energy Storage Science Technology, 2013(2): 146-151.
[14] 姚尔人, 王焕然, 席光. 一种压缩空气储能与内燃机技术耦合的冷热电联产系统 [J]. 西安交通大学学报, 2016, 50(1): 22-27.
YAO Erren, WANG Huanran, XI Guang. A novel combined cooling heating and power system with coupled compressed air energy storage and combustion engine [J]. Journal of Xi’an Jiaotong University, 2016, 50(1): 22-27.
[15] 沈维道, 童钧耕. 工程热力学 [M]. 4版. 北京: 高等教育出版社, 2007: 268-269.
[16] ROGERS A, HENDERSON A, WANG X, et al. Compressed air energy storage: thermodynamic and economic review [C]∥Power and Energy Society General Meeting. Piscataway, NJ, USA: IEEE, 2014: 1-5.
[17] SONNTAG R E, BORGNAKKE C, VAN WYLEN G J, et al. Fundamentals of thermodynamics [M]. 8th ed. New York, USA: Wiley&Sons Inc, 2003: 761.
[18] CENGEL Y A, BOLES M A. Thermodynamics: an engineering approach [M]. 4th ed. New York, USA: McGraw-Hill, 2002: 189.
[19] HAYNES W M, LIDE D R, BRUNO T J. Handbook of chemistry and physics [M]. 95th ed. Boca Raton, USA: CRC, 2014: 1096-1097.
ResearchontheWaterSprayingRateforanEnergyStorageSystemofIsothermalCompressedAir
HE Ziwei1,2, LUO Maji1,2, TU Zhengkai3
(1. Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan University of Technology, Wuhan 430070, China; 2. Hubei Collaborative Innovation Center for Automotive Components Technology, Wuhan University of Technology, Wuhan 430070, China; 3. State Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan 430070, China)
To research the effect of different parameters on the water spraying rate for an energy storage system of isothermal compressed air, a novel method was proposed to study the quasi-isothermal compression using a compression process with the polytropic exponent close to 1, where the water vapor, liquid water and air in the final state were assumed as an ideal mixture. The water spraying rate under different state parameters was researched according to the saturated water vapor pressure formula, the Dalton partial pressure theory and the thermodynamic parameters of the components. The results show that the heat transfer proportion increases with the pressure ratio and the water spraying rate. When the pressure ratio is 10 and the rotation speed is 100 r/min, the water spraying rate increases from 5.73 kg/s to 8.68 kg/s, and the proportion of heat transfer is increased by 5%. The pressure ratio, heat transfer efficiency and final temperature all have effects on the mass ratio of air to water. Moreover, results also show that when other conditions are constant, the rotation speed has almost no effect on the ratio of air to water. When the pressure ratio increases to 10, the heat transfer efficiency is 95% and the final temperature is 50 ℃, the mass ratio of air to water maintains at 0.86 when the rotation speed is 60, 100, 150 r/min, respectively. In all, lower pressure is unfavorable to the thermal storage of water.
energy storage of compressed air; isothermal compression; heat storage; saturated water vapor pressure
2017-06-15。 作者简介: 何子伟(1993—),男,硕士生;涂正凯(通信作者),男,研究员。 基金项目: 国家自然科学基金资助项目(51476119)。
时间: 2017-10-18
网络出版地址: http:∥kns.cnki.net/kcms/detail/61.1069.T.20171018.1632.010.html
10.7652/xjtuxb201801006
TK02
A
0253-987X(2018)01-0033-07
(编辑 荆树蓉)

