利用形式化方法的机电系统概率失效模式及影响分析

杨培林, 侯翌, 徐凯, 贾焕如

(西安交通大学机械工程学院, 710049, 西安)

利用形式化方法的机电系统概率失效模式及影响分析

杨培林, 侯翌, 徐凯, 贾焕如

(西安交通大学机械工程学院, 710049, 西安)

针对传统的失效模式及影响分析中依靠领域专家分析判断系统单元失效与系统故障之间的关系,分析烦琐、容易出错且难以计算故障概率的问题,将形式化技术引入机电系统失效模式及影响分析中,提出了基于概率模型检测的机电系统概率失效模式及影响分析方法。基于机电系统中的状态变迁,研究了机电系统行为过程的随机模型及其形式化表达,建立了面向概率失效模式及影响分析的系统形式化随机模型;基于连续随机逻辑对系统的潜在故障进行了形式化规约,构建了潜在故障的概率形式化规约表达式;利用概率模型检测器对系统的随机模型和潜在故障进行形式化验证,从而辨识单元失效与系统潜在故障之间的关系,并自动计算单元失效所导致的系统故障概率,提高了失效模式与影响分析的准确性和效率。该方法不仅可以借助概率模型检测迅速准确地识别单元失效与系统潜在故障之间的因果关系,还可以自动计算系统故障概率。将该方法应用于数控机床进给系统,成功辨识出了限位开关失效所导致的系统故障并计算出了故障概率,从而验证了方法的可行性。

机电系统;失效模式及影响分析;概率失效模式及影响分析;概率模型检测;可靠性评价

随着机电系统的集成度和复杂程度越来越高,系统的可靠性和安全性问题日显突出。由于机电系统的高度集成与强耦合,系统单元的失效不仅会降低系统的可靠性,还可能引发严重故障,造成巨大损失,因此在机电系统的设计过程中,应及时对所设计的系统进行失效模式及影响分析(failure modes and effects analysis,FMEA)。若在FMEA过程中能同时计算出单元失效所导致的系统故障概率,则称为概率FMEA[1](PFMEA)。PFMEA是后续系统风险评估和致命度计算的基础,对机电系统的可靠性评价具有十分重要的作用。

传统FMEA在实施时很大程度上依赖专家经验,工作量大,效率低,且无法获得单元失效所导致的系统故障概率。为此,很多学者对FMEA进行了研究,以改善其分析效果,包括:①计算机辅助FMEA[2-4],主要是通过表格自动填写来辅助人工完成FMEA;②基于定性推理[5-7]和定量推理[8-10]的FMEA方法,通过对系统组成单元因果行为的描述或通过数字仿真软件对每个潜在故障的仿真分析,实现FMEA自动化;③基于功能模型的FMEA[11-13],通过系统的功能角色模型,利用定性代数理论对系统的故障传播进行推理,以实现FMEA自动化。

以上研究尽管使FMEA的分析效率得以提高,但单元失效所导致的系统故障仍需依赖领域专家来确定,且无法计算单元失效所导致的系统故障概率。

概率模型检测是传统模型检测技术的扩展[14],是自动验证随机模型是否满足预期性质的一种形式化技术。概率模型检测不仅能够验证系统性质的正确性,还能够自动计算系统性质成立的概率,具体包括形式化建模、形式化规约和形式化验证3个环节。本文将形式化技术引入机电系统FMEA,建立了机电系统的形式化随机模型及潜在故障的概率形式化规约,利用概率模型检测器自动辨识单元失效与系统潜在故障之间的关系,并自动计算单元失效所导致的系统故障概率,实现了基于形式化方法的机电系统PFMEA。

1 机电系统形式化随机模型的建立

1.1 机电系统的状态变迁

依据机电系统设计过程中功能、行为及状态之间的映射关系[15-16],机电系统的功能可用功能载体的一系列状态变迁来表示。从状态变迁的角度,可将机电系统的功能执行过程看成离散事件动态系统。在状态变迁离散事件动态系中,“事件”是驱使系统状态变迁的原因,同时状态变迁又会产生新的“事件”。机电系统的功能执行过程是一种事件驱动下的状态变迁过程。例如,某系统中控制器发出“启动电机”指令是一种事件,该事件驱使电机由“停止”状态变为“旋转”状态,并产生新的事件“电机旋转”,这一新事件又会驱使与之连接的丝杠由“停止”状态变为“旋转”状态,如图1和图2所示。图中用“!”表达“事件的发生”(发送消息),用“?”表达“事件对状态变迁的驱动”(接收消息)。

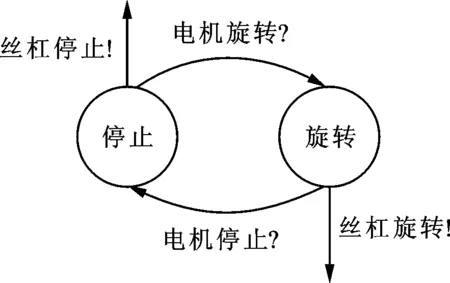
图2 丝杠的状态变迁过程

当考虑系统单元的失效时,状态变迁模型中还要考虑单元从正常状态向失效状态的变迁。例如,某传感器在正常情况下有“低电平”和“高电平”2种状态,在考虑故障时还会有“故障”状态,若分别用“00”“01”和“1”表示这3种状态,则传感器的状态变迁过程如图3a所示。

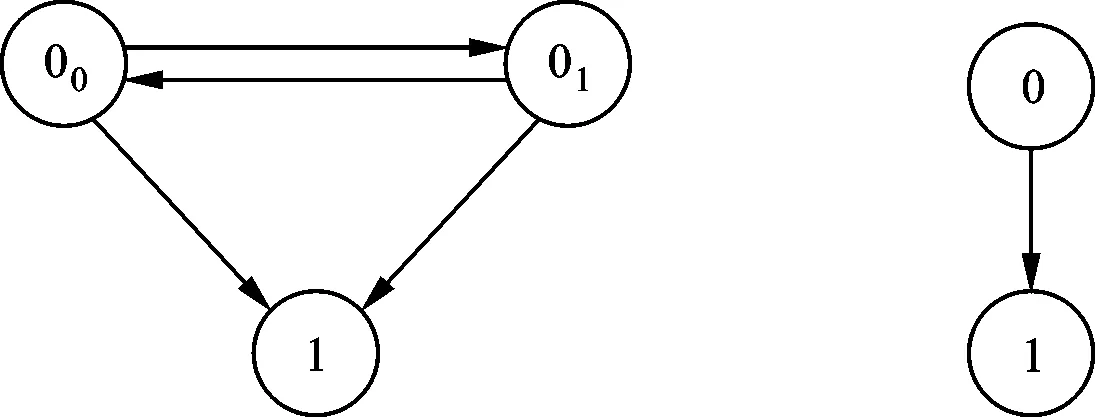
(a)3种状态变迁 (b)2种状态变迁图3 传感器的状态变迁过程

若不关注传感器正常情况下“00”与“01”之间的状态变迁,可将“00”和“01”2个状态合并,合并后的状态用“0”来代表,表示传感器处于正常状态。这时,图3a所示的状态变迁可简化为图3b所示的状态变迁,它反映了传感器在“正常”状态与“故障”状态之间的变迁过程。

机电系统各个单元状态的组合构成了系统的状态空间。若系统有n个单元,各单元的状态用集合Si(i=1,2,…,n)表示,则在各单元状态独立的情况下,系统的状态空间S=S1×S2×…×Sn。若单元状态不独立,则应从状态空间里剔除不合理的系统状态,例如2个单元在某种状态会出现碰撞,就应把对应的系统状态去除。机电系统的正常运行过程表现为状态空间中各状态之间的变迁过程。

1.2 状态转移率

机电系统在实际运行过程中,外部环境往往包含不确定性,导致机电系统的行为过程也具有一定的不确定性,例如,由于数控加工中心加工不同的工件时会有不同的加工工艺,导致其行为动作、运动速度、行程等相关工艺参数会随工件的不同而发生变化。因此,从统计学意义上讲,在机电系统的寿命周期内,机电系统行为过程中的状态变迁具有随机特性,可以认为状态变迁时间服从指数分布,并用状态变迁时间的数学期望T的倒数来表达状态转移率λ,即

另一方面,当考虑系统单元的失效时,状态变迁模型中还要考虑单元从正常状态向失效状态的变迁。单元失效时间通常按指数分布规律处理,这时的状态转移率即为单元的失效率。

由此可见,机电系统运行过程中状态(包括失效状态)之间的变迁可用连续时间马尔科夫过程(continuous time Markov chains,CTMC)来描述,即可利用CTMC来建立机电系统的随机模型。

1.3 形式化随机模型的建立

为了利用模型检测进行PFMEA分析,需要借助模型检测器提供的形式化建模语言对基于CTMC的机电系统随机模型进行形式化描述,建立机电系统的形式化模型。本文采用概率模型检测器(probabilistic symbolic model checker,PRISM)[17]提供的反应式模块形式语言来实现对机电系统随机模型的形式化表达。

PRISM建模语言所描述的模型由模块(modules)组成[18],模块包括状态变量和守卫(guard)命令。模块通过如下方式定义:

module name … end module

守卫命令由守卫(guard)和更新(update)组成,命令的形式为

[]guard->rate_1:update_1+…+rate_i:

update_i

其中:guard描述状态变迁需要满足的条件;update_i为状态变量的更新结果;rate_i为状态变迁(状态变量更新)过程中的状态转移率;方括号[]中可写入执行(action)标记,具有相同执行标记的命令是同步执行的。

例如对图1和图2所示的状态变迁,用PRISM可建立如下的形式化模型:

module motor∥电机模块

m:[0..1]init 0;∥电机状态变量,0静止,1转动

[motor_on]m=0->rate:(m′=1);∥电机由停止到旋转

[motor_off]m=1->rate:(m′=0);∥电机由旋转到停止

end module

module ballscrew∥丝杠模块

b:[0..1]init 0;∥丝杠状态变量,0静止,1转动

[motor_on]b=0->1 (b′=1);∥丝杠由停止到旋转

[motor_off]b=1->1 (b′=0);∥丝杠由旋转到停止

end module

利用以上方法建立的机电系统状态变迁模型称为机电系统面向PFMEA的形式化模型(formal model for probabilistic FMEA, FMPF)。机电系统中单元i产生失效模式j,而其他单元正常时所构成的形式化模型用FMPFij表示,反映单元i产生失效模式j时机电系统的状态变迁过程。

2 潜在故障的概率形式化规约

机电系统的潜在故障往往是因系统单元处于某种失效状态导致的,潜在故障可用系统单元的状态组合来表示。例如,在数控机床中,当刀具的位置状态为p且工件的位置状态为q时,机床将会产生碰撞,这一潜在故障可表示为“刀具处于位置状态p且工件处于位置状态q”。

利用PRISM进行模型检测时,潜在故障就是待验证的系统行为,因此需要将潜在故障通过概率时序逻辑公式进行形式化规约。对基于CTMC的形式化模型,PRISM用连续随机逻辑(continuous stochastic logics, CSL)[19]规约系统行为,因此本文对机电系统的潜在故障用CSL进行形式化规约。例如,对前述碰撞这一潜在故障,可用CSL规约为

P=?[F<=ttool=p& workpiece=q]

(1)

式(1)表示t个时间单位内机床发生碰撞故障,即刀具(tool)处于状态p并且工件(workpiece)处于状态q的概率。

基于上述规约方法,可以对机电系统任一可能的潜在故障建立其相应的概率形式化规约表达式,本文用FS(formal specification)表示。

3 基于概率模型检测的PFMEA

在建立了机电系统的形式化随机模型FMPF和潜在故障的概率形式化规约FS之后,即可用概率模型检测器(PRISM)进行形式化验证。对于形式化模型FMPFij,利用PRISM验证某一潜在故障的概率形式化规约FSk,就可获得在单元i出现失效模式j时系统出现故障k的概率,依此方法即可辨识单元失效与系统故障之间的关系,并能计算故障出现的概率,从而实现机电系统的PFMEA,如图4所示。

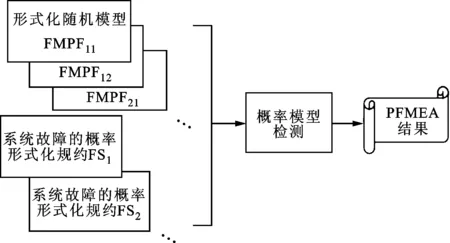
图4 基于概率模型检测的机电系统PFMEA

4 实例分析

图5为某数控机床Y、Z轴进给系统的结构简图,其中Y、Z轴电机带动工作台移动,限位开关检测并反馈Y、Z轴工作台的位置信息,数控系统控制电机的运动及停止。进给系统的干涉区域如图6所示,当Y、Z轴运动到干涉区时,B轴工作台与主轴发生干涉(即碰撞),为此进给系统不但配备有极限限位开关(防超程),还配备有干涉区限位开关(防干涉)。限于篇幅,这里对进给系统进行了必要的简化,例如忽略了进给系统中的传动机构,但这并不影响本文方法的验证。

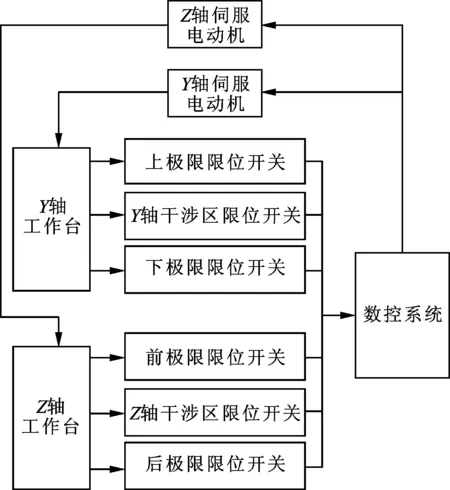
图5 某数控机床进给系统的原理结构图

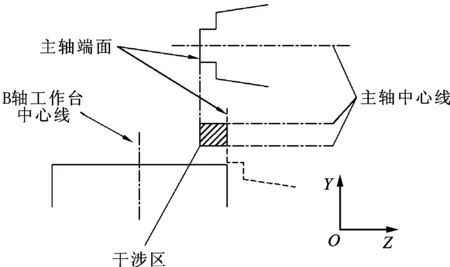
图6 进给系统干涉示意图

4.1 进给系统的形式化随机模型

本实例主要关注极限开关失效和干涉区开关失效对系统的影响,因此系统形式化随机模型主要包括功能正常条件下Y、Z轴工作台,Y、Z轴伺服电机和数控系统的形式化模型,以及失效情况下限位开关(极限开关和干涉区开关)的形式化模型。

Y轴工作台的状态包括“上极限”“干涉点”“下极限”,Z轴工作台的状态为“后极限”“干涉点”“前极限”。对Y、Z轴工作台,根据状态变迁过程用PRISM建立的形式化随机模型如下:

module wby∥Y轴工作台

wby:[0..2]init 0;∥Y轴工作台状态变量,0上极限,1干涉点,2下极限

[]wby=0&(wbz=0|wbz=1)-> rate1:(wby′=1);

[]wby=1&wbz=0->rate1:(wby′=2);

[]wby=2&wbz=0->rate1:(wby′=1);

[]wby=1->rate1:(wby′=0);

endmodule

module wbz∥Z轴工作台

wbz:[0..2]init 0;∥Z轴工作台状态变量,0后极限;1干涉区;2前极限

[]wbz=0&(wby=0|wby=1)-> rate1:(wbz′=1);

[]wbz=1&wby=0->rate1:(wbz′=2);

[]wbz=2&wby=0->rate1:(wbz′=1);

[]wbz=1->rate1:(wbz′=0);

endmodule

由于进给系统干涉区的存在,在正常状态下Y、Z轴工作台的运动不是独立的。例如,当Z轴工作台处于状态“前极限”时,Y轴工作台不能处于状态“干涉点”;当Y轴工作台处于状态“下极限”时,Z轴工作台也不能处于状态“干涉点”,如图7所示。在上面的形式化模型中,工作台状态之间的这种相互制约关系通过守卫条件来表示,例如模型中[]wby=0&(wbz=0|wbz=1)->rate1:(wby′=1)表示只有当Z轴工作台处于“后极限”或“干涉区”状态时,Y轴工作台才能从“上极限”变迁到“干涉点”。

图7 进给系统原理示意图

对于进给系统中的限位开关,正常情况下是在“低电平”和“高电平”2种状态之间变迁,在考虑失效后可表示为“正常”状态与“故障”状态之间的变迁,见图3。本例中的限位开关考虑“总是高电平输出”(模式1)和“总是低电平输出”(模式2)2种失效模式。对上极限开关,考虑失效模式1时的形式化模型如下:

module ts∥上极限开关

ts:[0..1]init 0;∥状态变量,0正常状态;1失效模式1

[]ts=0->rate2:(ts′=1);

endmodule

同理,可得其他限位开关及系统中Y轴伺服电机、Z轴伺服电机等单元用PRISM描述的形式化随机模型,限于篇幅不再列出。

4.2 进给系统故障的CLS规约

本实例关注的潜在故障如下:

(1)Y轴工作台到达上极限位置时Y轴电机继续运转,即Y轴上超程;

(2)Y轴工作台到达下极限位置时Y轴电机继续运转,即Y轴下超程;

(3)Z轴工作台到达前极限位置时Z轴电机继续运转,即Z轴前超程;

(4)Z轴工作台到达后极限位置时Z轴电机继续运转,即Z轴后超程;

(5)Y轴工作台和Z轴工作台都到达干涉区时,Y轴与Z轴电机未全部停运,即主轴箱与B轴工作台产生碰撞。

以上5种潜在故障对应的CLS表达式如下:

FS1:P=?[F<=twby=0&motory=0]∥Y轴工作台“上极限”且Y轴电动机“运转”

FS2:P=?[F<=twby=2&motory=0]∥Y轴工作台“下极限”且Y轴电动机“运转”

FS3:P=?[F<=twbz=0&motorz=0]∥Z轴工作台“后极限”且Z轴电动机“运转”

FS4:P=?[F<=twbz=2&motorz=0]∥Z轴工作台“前极限”且Z轴电动机“运转”

FS5:P=?[F<=twby=1&wbz=1&(motory=0|motorz=0|(motory=0&motorz=0))]∥Y、Z轴工作台“干涉点”且Y、Z轴电动机至少有一个“运转”

4.3 利用PRISM进行模型检测

在上述进给系统的形式化随机模型和潜在故障的CLS表达式中,设定工作台的状态转移率rate1为(30 min)-1,极限开关的失效率rate2为(10 a)-1,CLS中的时间t为3 a。利用PRISM对不同失效模式下的形式化随机模型和5种潜在故障进行概率模型检测,可获得各种潜在故障出现的概率,结果如表1所示,其中:0表示相应单元的失效不会导致该系统故障(故障概率为0);不为0的数字表示相应单元的失效单元可能导致系统故障及其出现的概率。

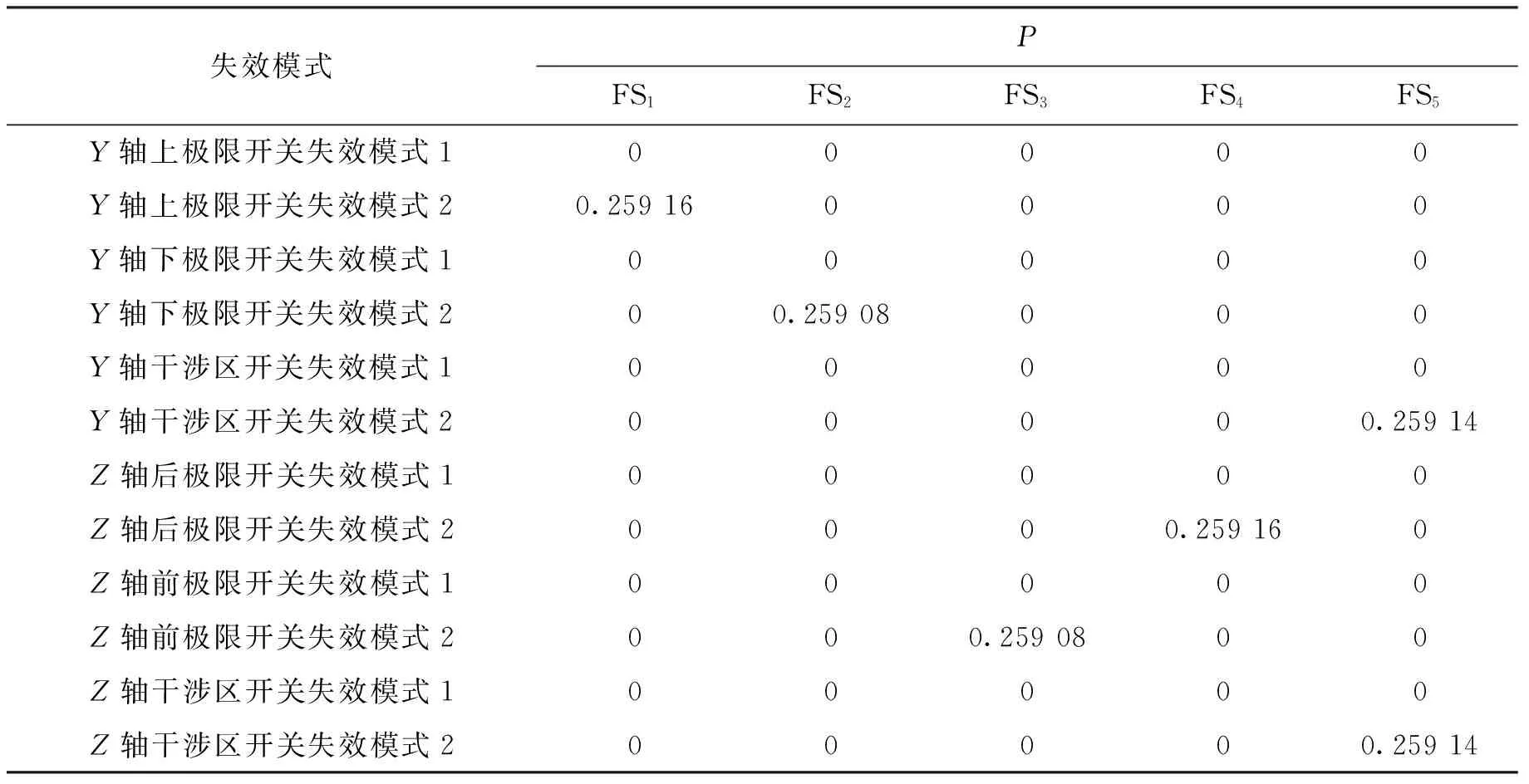
表1 概率模型检测结果

从表1中可看出:各种极限开关以及干涉区开关以失效模式1失效时,不会导致5种潜在故障的产生;当开关出现失效模式2时,有可能导致故障出现。这是因为失效模式2表现为低电平,不会发出报警信号(高电平),从而导致了潜在故障的产生。

从表1中还可以看出:Y轴上极限开关失效导致故障1的概率略大于下极限开关失效导致故障2的概率;Z轴后极限开关失效导致故障4的概率略大于前极限开关失效导致故障3的概率。这是由于Y、Z轴工作台存在干涉区(见图7),Y轴工作台处于上极限和Z轴工作台处于后极限的概率大于各自处于下极限和前极限的概率所致。

5 结 论

本文利用概率模型检测这一形式化方法的基本思想,根据机电系统运行过程的状态(包括正常状态和故障状态)变迁建立面向PFMEA的形式化随机模型,对系统的潜在故障进行概率形式化规约,然后借助概率模型检测工具PRISM对系统随机模型和潜在故障进行形式化验证,从而辨识单元失效模式与系统故障之间的关系,并自动计算单元失效所导致的系统故障概率,实现了基于形式化方法的机电系统PFMEA。

(1)机电系统运行过程中状态之间的变迁可用连续时间马尔科夫过程CTMC来描述,即可利用CTMC建立机电系统的随机模型,并可用PRISM建模语言进行形式化表达。

(2)机电系统的潜在故障可以通过连续随机逻辑CSL进行形式化规约,利用基于CSL的概率形式化规约表达式可以计算系统故障发生的概率。

(3)本文提出的PFMEA方法基于概率模型检测,是一种形式化方法,该方法不仅可以借助概率模型检测迅速准确地识别单元失效与系统潜在故障之间的因果关系,还可以自动计算系统故障概率,从而可为后续机电系统风险评估和致命度计算奠定基础。

[1] ALJAZZAR H, FISCHER M, GRUNSKE L, et al. Safety analysis of an airbag system using probabilistic FMEA and probabilistic counterexamples [C]∥Proceedings of International Conference on Quantitative Evaluation of Systems. Piscataway, New Jersey, USA: IEEE, 2009: 299-308.

[2] KARA-ZAITRI C, KELLER A, FLEMING P. A smart failure mode and effect analysis package [C]∥Proceedings of Annual Reliability and Maintainability Symposium. Piscataway, New Jersey, USA: IEEE, 1992: 414-421.

[3] 赵廷弟, 孙琳玲, 屠庆慈. 计算机辅助FMECA软件模型 [J]. 北京航空航天大学学报, 2000, 26(1): 118-121.

ZHAO Tingdi, SUN Linling, TU Qingci. Software model for computer-aided FMECA [J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(1): 118-121.

[4] 石真真, 刘更, 吴立言. 计算机辅助故障模式、影响及危害性分析研究 [J]. 机械与电子, 2011(6): 11-15.

SHI Zhenzhen, LIU Geng, WU Liyan. Research on computer assisted failure mode effect and criticality analysis [J]. Machinery & Electronics, 2011(6): 11-15.

[5] LEE M H, ORMSBY A R T. Qualitatively modelling the effects of electrical circuit faults [J]. Artificial Intelligence in Engineering, 1993(8): 293-300.

[6] PRICE C J, HUNT J E, LEE M H, et al. A model-based approach to the automation of failure mode effects analysis for design [J]. Journal of Automobile Engineering, 1992, 206(44): 285-291.

[7] 赵廷弟. 故障模式影响分析专家系统 [J]. 北京航空航天大学学报, 1999, 25(5): 611-614.

ZHAO Tingdi. Failure model effect analysis expert system [J]. Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(5): 611-614.

[8] MONTGOMERY T A, MARKO K A. Quantitative FMEA automation [C]∥Proceedings of Annual Reliability and Maintainability Symposium. Piscataway, New Jersey, USA: IEEE, 1997: 226-228.

[9] 沈颂华, 李瑛, 康锐. 航空电源系统FMEA自动化技术研究 [J]. 北京航空航天大学学报, 1997, 23(6): 805-809.

SHEN Songhua, LI Ying, KANG Rui. Study of FMEA automation technique for airborne power system [J]. Journal of Beijing University of Aeronautics and Astronautics, 1997, 23(6): 805-809.

[10] THROOP D R, MALIN J T, FLEMING L D. Automated incremental design FMEA [C]∥Proceedings of Aerospace Conference. Piscataway, New Jersey, USA: IEEE, 2001: 3451-3458.

[11] HAWKINS P G, WOOLLONS D J. Failure modes and effects analysis of complex engineering systems using functional models [J]. Artificial Intelligence in Engineering, 1998(12): 375-397.

[12] 王明凯, 邱静, 钱彦岭, 等. 用于自动故障模式影响分析的系统功能角色模型 [J]. 兵工自动化, 2003, 22(2): 40-44.

WANG Mingkai, QIU Jing, QIAN Yanling, et al. Role model of system function for automated failure mode and effect analysis [J]. Ordnance Industry Automation, 2003, 22(2): 40-44.

[13] 张海, 钱彦岭, 邱静. 基于功能角色模型的反馈系统故障模式影响 [J]. 国防科技大学学报, 2004, 26(1): 99-102.

ZHANG Hai, QIAN Yanling, QIU Jing. Analysis of the failure modes and effects of the feedback systems using functional role models theory [J]. Journal of National University of Defense Technology, 2004, 26(1): 99-102.

[14] KWIATKOWSKA M. Model checking for probability and time: from theory to practice [C]∥Proceedings of 18th Annual IEEE Symposium on Logic in Computer Science. Piscataway, New Jersey, USA: IEEE, 2003: 351-360.

[15] UMEDA Y, ISHII M, YOSHIOKA M, et al. Supporting conceptual design based on the function-behavior-state modeler [J]. Artificial Intelligence for Engineering Design Analysis and Manufacturing, 1996, 10(4): 275-288.

[16] 杨培林, 徐凯, 薛冲冲, 等. 基于IDEF的复杂机电系统状态解析 [J]. 机械设计与制造, 2015(9): 49-51.

YANG Peilin, XU Kai, XUE Chongchong, et al. State analysis of complex electrical mechanical system based on IDEF [J]. Machinery Design & Manufacture, 2015(9): 49-51.

[17] KWIATKOWSKA M, NORMAN G, PARKER D. PRISM 4.0: verification of probabilistic real-time systems [C]∥Proceedings of the 23rd International Conference on Computer Aided Verification. Berlin, Germany: Springer, 2011: 585-591.

[18] ALUR R, HENZINGER T A. Reactive modules [J]. Formal Methods in System Design, 1999, 15(1): 7-48.

[19] AZIZ A, SANWAL K, SINGHAL V, et al. Verifying continuous time Markov chains [C]∥Proceedings of the 8th International Conference on Computer Aided Verification. Berlin Germany: Springer, 1996: 269-276.

ProbabilisticFailureModesandEffectsAnalysisforElectromechanicalSystemsBasedonFormalMethod

YANG Peilin, HOU Yi, XU Kai, JIA Huanru

(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

In conventional failure modes and effects analysis (FMEA), the relations between component failures and system faults are analyzed and determined by domain experts, which is tedious, error-prone, and difficult to obtain the probabilities of the faults. In this paper, formal methods are introduced to FMEA for electromechanical systems and an approach to probabilistic FMEA (PFMEA) for electromechanical systems based on probabilistic model checking is proposed. Based on the state transitions in electromechanical systems, probabilistic model and its formal representation for the behavior process of the systems are studied and the formal probabilistic models for PFMEA are established. Continuous stochastic logic (CSL) formulas are employed to make formal specification of the potential faults in electromechanical systems, and the formal probabilistic specifications of potential fault are given. Formal verification is conducted for the system probabilistic models and potential faults, thereby the relations between the component failures and the potential system faults are identified. Moreover, the probabilities of the faults caused by component failures are calculated, so the efficiency and accuracy of the PFMEA are improved. By means of the approach presented in the paper, the causal relations between component failures and system faults are determined quickly and accurately, and the probabilities of the system faults are computed automatically. This approach is applied to the feed system of a CNC machine tool, and the system faults caused by limit switches and the probabilities of the faults are identified successfully, which demonstrates the feasibility of this approach.

electromechanical system; failure mode and effects analysis; probabilistic failure mode and effects analysis; probabilistic model checking; reliability evaluation

2017-07-07。 作者简介: 杨培林(1963—),男,教授。 基金项目: 国家自然科学基金资助项目(51375365)。

时间: 2017-10-20

网络出版地址: http:∥kns.cnki.net/kcms/detail/61.1069.T.20171020.1622.010.html

10.7652/xjtuxb201801001

TH122

A

0253-987X(2018)01-0001-07

(编辑 葛赵青)