全息波导元件的光线追迹及误差分析
高 阳, 何永学, 赵龙波, 谢 意, 康明武
(1.光电控制技术重点实验室,河南 洛阳 471000; 2.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000; 3.中国人民解放军93787部队,北京 100076)
全息波导元件的光线追迹及误差分析
高 阳1,2, 何永学3, 赵龙波2, 谢 意1,2, 康明武1,2
(1.光电控制技术重点实验室,河南 洛阳 471000; 2.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000; 3.中国人民解放军93787部队,北京 100076)
全息波导元件的设计通常会分解为光栅设计和波导设计,这种设计过程并不直观,且不适用于加工误差分析。为了解决上述问题,提出一种全息波导元件的综合分析方法,以二维出瞳拓展的全息波导显示系统为例,针对波导上下表面不平行度、光栅结构参数进行误差分析,以便了解上述误差对成像质量的影响。通过对模型参数的误差分析,对实际的生产加工过程提出有意义的精度指导。
波导光学; 衍射光学; 全息波导; 误差分析
0 引言
全息波导元件利用光栅的衍射现象和波导的全反射现象进行光线传输和成像,具有结构小、重量轻、视场大、出瞳大的优点,被认为是新一代的显示技术。全息波导显示原理在近几年被国内外学者深入研究[1],并在头戴式显示设备和军用显示器等领域得到了应用[2-5]。
全息波导元件的设计综合了基于衍射光学理论的光栅结构设计[6-9]和基于几何光学的波导布局设计。理想的全息波导元件没有光焦度,因而不会产生像差。而实际加工过程中,光栅的周期、光栅矢量方向、波导板上下表面的平行度等结构参数会与设计值产生误
1 光线在光栅和波导中的传播
光线与全息波导元件的相互作用包括如下3类:1) 光线在入射和出射波导时,在空气-波导界面的折射现象;2) 光线在波导内的全反射现象;3) 光线在光栅区的衍射现象。
光线的折射和全反射过程较为直观,因此本文中省去相应的说明,仅针对光线在光栅区域的衍射现象进行分析。为方便分析,假设光栅所处的波导下表面与X-Y平面平行,波导的不平行度由上表面的倾斜来体现。光线在光栅区的衍射现象如图1所示。

图1 光线在波导光栅处衍射图Fig.1 Diffraction on waveguide grating
光线的描述采用波矢K表述,波矢的大小称为波数K=2π/λ,λ是光线在当前介质中的波长,波矢的方向即为光线传播方向。矢量分析中涉及到波导上下表面的单位法向量,其向量方向定义为:箭头朝向波导介质内部,即波导上表面的单位法向量朝下,波导下表面的单位法向量朝上。
由于光栅的引入,其光线的波矢分析过程需要将波矢分为x,y,z3个分量进行分析,并分别以x,y,z作为上标进行标注,衍射前后波矢关系为
(1)
(2)
(3)
(4)
式中:i为设计的衍射级次;2π/Λx为光栅在Y-Z平面的水平周期;2π/Λy为光栅在X-Z平面的水平周期。事实上,利用光栅矢量的概念会对上式有更好的理解:光栅矢量2π/Λy形式与波矢类似,如图1所示,其矢量大小为2π/Λ,矢量方向与光栅条纹垂直,并位于光栅层平面,矢量方向与设计衍射级次的偏折方向一致。与反射和折射现象不同,衍射前后界面平行的波矢分量不再守恒,而是相差i个光栅矢量值,光栅对光线传播方向的调控由此体现。
在实际设计过程中,全息光栅的周期小于入射光波长,由于光栅会对一束光线产生出多个衍射级次,非设计的衍射级次通常会采用一些方法进行抑制,使得光线按照指定的衍射级次和衍射角度继续传播,在后文的误差分析过程中,均假定光线沿着指定衍射级次和角度进行传播,而不再考虑光线沿着非设计的衍射级次进行传播。
2 光线在转折光栅区的传播
波导元件的误差分析,涉及到光线的追迹:从光线进入波导,并依次与入射光栅G1、转折光栅G2和出射光栅G3发生作用,最终从波导中输出。
对于G2光栅而言,直接追迹的方法是不可行的。如图2所示,从G1衍射而来的光线与G2首次发生作用,部分光线因衍射现象而偏折(红色实线R1),剩余部分光线则全反射继续传播(黑色实线R0),由此产生两条光线:衍射后的光线R1在波导中折返传播一次后,其部分光线再次衍射并偏折,其余部分全反射传播(红实线后的红色虚线);未发生衍射的光线R0在波导中折返传播一次后,部分光线衍射偏折(黑实线后的红色虚线),剩余光线继续全反射传播(黑实线后的黑色虚线)。由于上述传播现象,一条入射光线在该区域的传播过程中,光线数会按照指数形式增长,使得直接光线追迹不再可行。

图2 光线在转折区光栅G2处的传播图Fig.2 Light propagation on grating G2 in holographic waveguide
2.1 理想情况下的传播
当波导上下平面绝对平行时,G2光栅区域中传播的所有光线,具有特定的空间分布规律:光线在波导内折返传播过程中,多次的反射和衍射的综合效果使光线的传播路径在空间交织成二维网格图案,如图3所示。由此,可采用如下分析方法定义:将从G1光栅朝向G2光栅传播光线的一次折返传播定义为P向单位传播距离(蓝色),将从G2光栅朝向G3光栅传播光线的一次折返传播定义为Q向单位传播距离(红色),按照俯视图下光线传播方向则对于任意一个P向传播光线P(i,j),它是由上一个P向传播光线P(i-1,j)与G2光栅发生全反射的部分光线以及上一个Q向传播光线Q(i,j-1)与G2光栅发生衍射的部分光线的叠加;同样,对于任意一个Q向传播光线Q(i,j),它是由上一个P向传播光线P(i-1,j)与G2光栅发生衍射的部分光线以及上一个Q向传播光线Q(i,j-1)与G2光栅发生全反射的部分光线的叠加。用公式表示为
(5)
式中,ηp和ηq分别是P向光线和Q向光线与G2光栅作用的衍射效率。

图3 理想条件下全息波导元件的光线传播图Fig.3 Light propagation in holographic waveguide under ideal condition
2.2 波导上下表面不平行情况下的传播
当波导上下平面不平行时,情况将更加复杂,衍射和全反射的前后顺序将对最终光线的出射造成不同影响,其传播光路俯视图也不再是简单的二维网格,对此,需要在满足分析精度的前提下,进行一定程度的简化。假设G2光栅位于波导下表面处,同一条入射光线K,通过不同传播路径后对应了光线K16和K26,见图4,在光线的单位传播距离中,分别会与波导上表面和波导下表面(或者光栅面)作用一次,因而图3中光线的单位传播距离不再由1个虚线段代表,而是由2个虚线段代表。
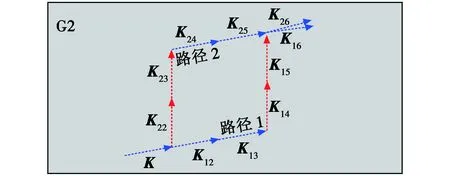
图4 G2光栅内两条光线传播路径对比Fig.4 Differences between the two paths in grating G2
为此,分别计算K光线经过路径1和路径2后的光线矢量K16和K26,并进行对比分析。
2.2.1 路径1
已知入射光线波矢K,波导下表面水平,波导上表面倾斜,上表面的单位法向矢量为n,即
(6)
式中,nz远大于nx和ny,经过下表面反射后
(7)
随后经过上表面反射
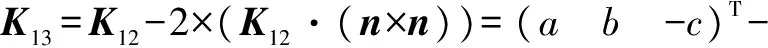
(8)
其中
q=2(anx+bny-cnz)≈-2cnz
。
(9)
波矢K13随后与光栅发生衍射作用
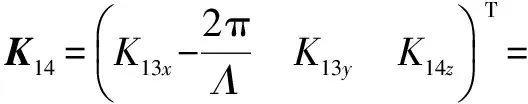
(10)
随后经过上表面反射
K15=K14-2×(K14·(n×n))=
(11)
其中

。
(12)
最后,经过光栅衍射后
。
(13)
2.2.2 路径2
同样
(14)
经过光栅衍射后
(15)
随后,经过波导上表面反射后
(16)
其中
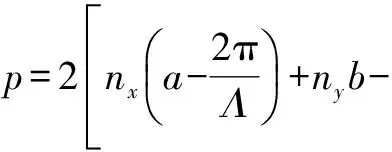
(17)
随后,再次受到光栅衍射
(18)
随后,受到波导上表面衍射
(19)
其中
P=2[nx(a-pnx)+ny(b-pny)-nz·
(20)
最终,经波导下表面反射
(21)
易知
K16≈K26
。
(22)
也就是说,光线在G2光栅区域传播过程中,多次衍射对最终出射光线波矢产生的累积误差远小于多次全反射传播产生的累计误差,在实际的全息波导元件误差分析中,图3所示的光路路径可以进一步简化为图5所示的光路路径。基于该简化,全息波导元件中光线的传播分析可以进行直接光线追迹,并进行误差分析。

图5 简化后的全息波导元件的光线传播图Fig.5 Simplified light propagation in holographic waveguide
3 全息波导元件加工误差分析
根据上述分析,通过Matlab进行仿真,讨论波导板不平行度和光栅结构误差对出射光线角分辨率的影响。即通过对比特定视场光线(中心视场,以及10°的上下左右4个视场)的理想出射角度与误差条件下的实际出射角度的差异。
仿真中入射光线的真空波长525 nm,3个光栅均为反射式光栅,且均位于波导元件的下表面,模型参数定义如表1所示。

表1 全息波导元件分析模型参数
仿真中视场光线定义如表2所示。
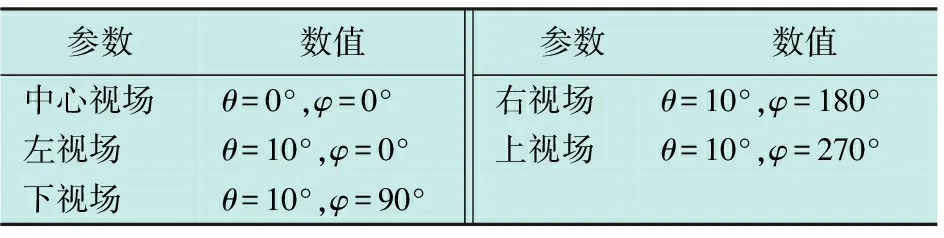
表2 视场光线定义表
角度定义如图6所示。θ为入射光线与Z轴的夹角,φ为入射光线所在入射面与X轴的夹角。

图6 仿真模型视场角定义Fig.6 Definition of FOV in simulation model
3.1 波导板不平行度分析
仿真中假定波导下表面与X-Y面平行,上表面倾斜。为了更全面了解波导板不平行度对成像质量的影响,分别针对波导上表面绕X轴倾斜、波导上表面绕Y轴倾斜,以及波导上表面绕X和Y轴角平分线的倾斜3种情况进行分析讨论,不平行度与出射光线角分辨率关系分别如图7所示。
可以看出,波导不平行度在±30″范围内时,不同视场光线的角分辨率与波导不平行度可认为是线性关系;波导不平行度与视场光线角分辨率的关系对波导不平行度的方向并不敏感。
对比不同视场光线:下视场和右视场光线受到波导不平行度的影响约为0.83′角分辨率/1″波导平行度,中心视场光线受到波导不平行度的影响约为0.54′角分辨率/1″波导平行度,而上视场和左视场光线受到波导不平行度的影响约为0.37′角分辨率/1″波导平行度。不同视场光线角分辨率对波导不平行度的敏感性不同,是由于不同视场光线在波导中传播的折返次数不同导致:下视场和右视场光线在波导内的折返次数较多,因此波导不平行度对出射光线角分辨率的影响较大,上视场和左视场光线在波导内的折返次数较少,因此波导不平行度对出射光线角分辨率的影响较小。

图7 波导板的不平行度对5个视场出射光线角分辨率的影响Fig.7 Effect of waveguide nonparallelism on 5 typical views’ angular resolutions
3.2 光栅结构误差分析
光栅结构的误差主要包括了光栅周期误差和光栅矢量方向的误差。当光栅加工周期与设计周期产生差距后,出射光线也将受其影响。光栅G1,G2和G3周期变化对出射光线角分辨率的影响分别如图8所示。光栅周期在±2 nm范围内时,不同视场光线的角分辨率与光栅周期偏差可认为是线性关系;光栅周期误差对不同视场光线影响的区别并不显著。
根据第1章中光栅衍射现象的描述,光栅周期越大,周期误差对出射光线角分辨率的影响越小,周期偏差周期误差这一规律在图8中也得到体现:其中G1和G3光栅周期为450 nm,周期偏差对不同视场光线的角分辨率的影响约为9′角分辨率/1 nm;G2光栅周期318.2 nm,周期偏差对不同视场光线的角分辨率的影响约为18′角分辨率/1 nm。
当光栅G1,G2和G3角度方向与设计产生差距后,对出射光线角分辨率的影响分别如图9所示。光栅角度偏差在±30′范围内时,不同视场光线的角分辨率与光栅角度失配可认为是线性关系;光栅角度失配对不同视场光线影响的区别并不显著。
由于G2光栅周期小,其具有更大的光栅矢量,由此角度偏转对出射光线角分辨率的影响越大,这一规律在图9中也得到体现:G1和G3光栅角度失配对不同视场光线的角分辨率的影响约为1.2′角分辨率/1 nm;G2光栅角度失配对不同视场光线的角分辨率的影响约为1.7′角分辨率/1 nm。

图8 光栅周期失配与5个视场出射光线角分辨率的关系Fig.8 Effect of grating perido mismatch on 5 typical views’ angular resolutions

图9 光栅矢量方向偏移与5个视场出射光线角分辨率的关系Fig.9 Effect of grating vector direction deviation on 5 typical view’ angular resolutions
4 结束语
综上,首先对光线折射、全反射和衍射现象进行表达和描述;针对光线在转折光栅区传播特性导致的追迹光线条数呈指数增加的难题,分别在理想情况和考虑波导上下表面不平行情况下进行公式分析讨论和简化,以此为基础,对波导元件加工误差进行分析。
通过仿真分析发现,波导板不平行度对不同视场光线的影响程度具有明显差异,光线在波导中折转传播越多,其角分辨率越差;不同波导倾斜方向对光线角分辨率影响较小。光栅结构误差(光栅周期和光栅条纹方向)对不同视场光线影响程度近似;更小周期光栅的结构误差(光栅周期和光栅条纹方向)对光线角分辨率影响更大。
本文提出的分析方法对深入理解全息波导成像过程有着重要意义,同时,通过对模型参数的误差分析,可以对实际的生产加工过程提出有意义的精度指导。后续工作中,也将根据本文仿真结果进行实验验证。
[1] 周海宪,程云芳.全息光学———设计、制造和应用[M].北京:化学工业出版社,2006.
[2] MALCOLM H.The use of optical waveguides in Head Up Display(HUD)applications[C]//Proceedings of SPIE, 2013,8736:87360E-1-87360E-14.
[3] TAKASHI O,KATSUYUKI A,MIEKO K,et al.High-luminance see-through eyewear display with novel volume hologram waveguide technology[C]//SID Symposium Di-gest of Technical Papers,2015:192-195.
[4] TAPANI L.Diffractive optics for virtual reality displays[J].Journal of the SID,2006,14(5):467-475.
[5] 刘玉杰,李文强,丁全心,等.全息波导板构型优化[J].电光与控制,2015,22(2):69-72.
[6] 周家武,巩华,康明武,等.波导体全息光栅衍射光谱范围一致性研究[J].电光与控制,2015,22(1):80-83.
[7] MOHARAM M G,ERIC B,DREW A.Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J].Journal of the Optical Society of America A,1995(12):1068-1076.
[8] MOHARAM M G,POMMET D A,GRANN E B,et al.Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings:enhanced transmittance matrix approach[J].Journal of the Optical Society of America A,1995(12):1077-1086.
[9] LI L.Use of Fourier series in the analysis of discontinuous periodic structures[J].Journal of the Optical Society of America A,1996(13):1870-1876.
[10] LEON E,MICHAEL M,MICHEAEL G,et al.Planar configuration for image projection[J].Applied Optics,2006, 45(17):4005-4011.
[11] LEE C K.TAEWON L,MIN S W.Analysis and design of wedge projection display based on ray tracing method[C]//Proceedings of SPIE,2012,8498:84980H-1-84980H-10.
RayTracingandErrorAnalysisofHolographicWaveguide
GAO Yang1,2, HE Yong-xue3, ZHAO Long-bo2, XIE Yi1,2, KANG Ming-wu1,2
(1.Science and Technology on Electro-Optic Control Laboratory,Luoyang 471000,China; 2.Luoyang Institute of Electro- Optical Equipment,AVIC,Luoyang 471000,China; 3.No.93787 Unit of PLA,Beijing 100076,China)
The design process of holographic waveguide display system is usually divided into grating design and waveguide design,which is unintuitive and incapable for machining error analysis.Therefore,we propose a new comprehensive method for holographic waveguide design,which analyzes the diffraction process and transmission process of light synthetically.Taking the 2-D exit-pupil expander holographic waveguide display system as an example,analysis is made to the error caused by the waveguide wedge and grating parameters.In addition,their influence on imaging quality is also analyzed.This analysis method can provide the required accuracy for manufacture process.
waveguide optics; diffraction optics; holographic waveguide; error analysis
高阳,何永学,赵龙波,等.全息波导元件的光线追迹及误差分析[J].电光与控制,2017,24(7):75-80.GAO Y,HE Y X,ZHAO L B,et al.Ray tracing and error analysis of holographic waveguide[J].Electronics Optics & Control,2017,24(7):75-80.
V271.4
A
10.3969/j.issn.1671-637X.2017.07.016
2016-11-18
2016-12-11
航空科学基金项目(20155169017)
高 阳(1988 —),男,河南平顶山人,博士,工程师,研究方向为全息显示和微纳光学技术。差,并进一步对理想成像产生影响[10]。对于二维出瞳拓展的全息波导元件,其转折光栅区G2处的二次衍射现象会使波导板的平行度误差分析变得更加复杂。事实上,针对光栅结构的误差分析[10]和波导平行度的误差分析[11]都有文献可循,而综合考虑光栅误差和波导误差的研究工作则还未发现。

