高超声速飞行器机翼关键部件损伤特性分析

邵 鹏， 王玉惠,2， 吴庆宪， 甄武斌

(1.南京航空航天大学自动化学院，南京 211106； 2.光电控制技术重点实验室，河南 洛阳 471000)

高超声速飞行器机翼关键部件损伤特性分析

邵 鹏1， 王玉惠1,2， 吴庆宪1， 甄武斌1

(1.南京航空航天大学自动化学院，南京 211106； 2.光电控制技术重点实验室，河南 洛阳 471000)

分析了高超声速飞行器机翼关键部件的损伤演化及飞行器飞行动态对损伤的影响。在建立了高超声速飞行器机翼关键部件损伤动力学模型、飞行器动力学模型以及对机翼关键部件载荷应力分析的基础之上，依次分析了飞行器飞行高度、速度、迎角以及控制舵面偏角等飞行器变量对机翼关键部件损伤动态特性的影响，以确定影响损伤的关键变量。仿真结果表明，相对于其他变量，飞行器迎角对机翼关键部件损伤的影响是最大的。基于此结果可得出当飞行器进行高超声速飞行时，从保证飞行安全与延长使用寿命的角度来看，应尽量限制飞行迎角大小。所得结论为实际工程中结构可靠性设计提供了有价值的参考。

高超声速飞行器； 机翼； 损伤动力学模型； 损伤动态特性

0 引言

高超声速飞行器指飞行马赫数超过5的先进飞行器，其巡航马赫数可达10以上，飞行高度通常在30 km以上。在飞行过程中,随着飞行速度的增加以及飞行姿

目前国内外关于机翼损伤分析的研究多数是对特定试件进行机械测试或是用有限元方法进行分析。文献[5]采用无损检测的方法对机翼结构在交变应力作用下的损伤演化进行了分析；文献[6-7]提出用有限元模拟机翼振动响应的方法估算机翼振动功率谱密度和损伤分布的方法；文献[8-9]应用有限元软件对翼梁试件结构进行裂尖应力强度因子分析；文献[10]采用名义应力法及累积损伤理论估算翼梁疲劳裂纹形成寿命；文献[11]利用Fastran模型来模拟机翼结构在变幅载荷作用下的损伤演化情况。以上文献的研究对象均为普通飞行器机翼，且仅从机翼受力的角度来分析机翼特定部件的损伤，并没有对飞行器不同的飞行状态对机翼损伤的影响做定性分析。为了获得高超声速飞行器各个飞行输出量对机翼关键部件损伤的影响，本文在建立了机翼关键部件损伤动力学模型、飞行器动力学模型以及对机翼关键部件载荷应力分析的基础之上，分别对飞行器飞行速度、高度、迎角以及舵面偏角对机翼关键部件损伤动态特性的影响进行了定性分析，以确定对损伤演化影响最大的飞行器输出量，为飞控系统以及飞行器结构设计提供了一定的参考。

1 机翼关键部件损伤动力学建模

为了能较准确地模拟出机翼关键部件即翼梁根部在飞行过程中的损伤演化情况，本文采用细微疲劳裂纹长度来表征翼梁根部的损伤情况，该裂纹演化模型可由非线性微分方程表示，即

(1)

(2)

式中:a为机翼翼梁根部的裂纹长度；σmax为翼梁根部在一次载荷循环中受到的最大应力；σO为裂纹临界张开应力；η为衰减系数；σoss为裂纹临界张开应力调节函数；C,m为材料Paris常数;函数F(a)=[sec(πa/2w)]1/2为结构几何因子，w为结构几何常数；U(·)表示符号函数。

式(2)中，U(σoss-σO)和σoss分别为

(3)

(4)

式中，部分参数有如下形式

(5)

其中:σmin为翼梁根部在一次循环载荷中受到的最小应力；ε∈[1,3]为约束因子；σyield,σuts分别为部件材料的屈服应力与极限应力。

由以上裂纹演化模型可以看出，机翼翼梁根部裂纹增长速率主要由结构受到的循环载荷应力σmax,σmin，裂纹张开应力σO，载荷作用频率以及材料特性参数决定,该损伤模型能够较直观地反映出裂纹随着动态载荷作用时间的增加而演化的情况。

2 机翼关键部件载荷应力分析

为了计算翼梁根部受到的循环载荷应力σmax,σmin，首先需要结合机翼结构对翼梁根部进行载荷应力分析。

由于高超声速飞行器机翼结构比较复杂，因此对机翼作受力分析时通常将机翼简化为壁梁结构，对其关键部件的受力分析主要是针对翼梁根部所受拉压应力和剪切应力进行分析。为了保证较好的波阻特性，该类机翼通常采用薄对称菱形翼型，其基本受力分析如图1所示。

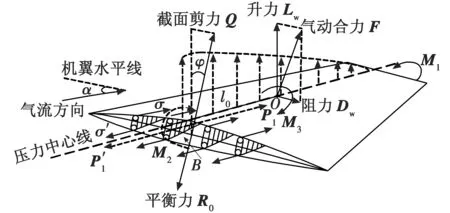
图1 机翼受力分析示意图Fig.1 Force analysis of the wing

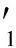
设4根翼梁的高度分别为H1,H2,H3,H4,在力矩M1作用下翼梁根部受到的平均拉-压应力为

(6)

式中:Hm为翼梁平均高度；IZ1为翼梁截面矩，即

(7)

式中:δ1为翼梁腹板厚度以及缘条厚度；δ2为缘条宽度，如图2所示。

图2 机翼截面剪力示意图Fig.2 The shear force analysis of the wing section

假设机翼气动焦点O到机翼重心的距离可忽略，则弯曲力矩M1可表示为

M1=[(Lw-Mwg)cosα+Dwsinα]l0

(8)

式中:l0为气动焦点O点沿压力中心线到翼根的距离;Mw为机翼自重;g为重力加速度。

类似地，弯曲力矩M3由垂直于翼面的合力产生，在弯曲力矩M3作用下翼梁根部受到的平均拉-压应力σ2可表示为

(9)

式中,截面矩与弯曲力矩为

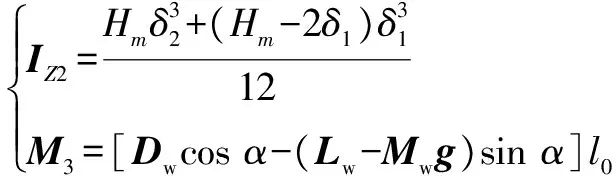
(10)

作用于翼梁根部的截面剪力Q由M1的反作用矩M2产生，其平衡力为R0，有

(11)

τQ1,τQ2为翼梁根部所受纵向切应力和横向切应力，平均大小分别为τQ1和τQ2，即

(12)

式中：φ表示截面剪力Q与翼面法线间的夹角;A1～A4分别为4根翼梁的截面面积，有

(13)

式中,Hi为对应编号翼梁的高度。

以上各式中，机翼升力Lw和阻力Dw为

(14)

式中:ρ为大气密度，表示为高度的函数；V为飞行速度；Sw为单机翼面积；CL,CD分别为机翼升力系数和阻力系数，均表示为迎角α、速度V以及气动舵面偏角的函数。

在计算机翼翼梁根部所受拉压应力与剪切应力的合力情况时，利用应力叠加原理，其合力与各分应力的关系为

。

(15)

根据材料力学的相关知识，可将拉压应力和剪切应力共同作用对材料的损伤等效为一个单向应力作用对材料的损伤，该单向应力称为相当应力[12]，由第三强度理论得到相当应力σE为

(16)

该相当应力σE即为翼梁根部受到的载荷应力。由于飞行器在飞行过程中受到复杂的气动干扰使得气动参数存在一定的不确定，从而导致机翼会受到一定频率的循环载荷作用，根据该循环载荷的动态特性可将σE在变化中的峰、谷值表示为翼梁根部在某时刻受到的σmax和σmin，即为动态载荷。

3 高超声速飞行器动力学模型

由以上分析可以看出，机翼翼梁根部的载荷应力计算涉及到了多个飞行器动态变量，如飞行高度、速度、迎角、舵面偏角等，因此需要应用高超声速飞行器的动力学模型进行分析。由于在高超声速飞行器飞行过程中侧滑运动和偏航运动对机翼受力的影响较小，因此可将侧滑角和偏航角速率置0。本文考虑如下高超声速飞行器动力学模型

(17)

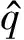
4 机翼关键部件损伤动态特性分析

综合以上各部分的分析，可将高超声速飞行器机翼关键部件损伤动态特性分析过程归纳为：首先通过飞行器动力学模型得到飞行器输出量(如H,V,α,δe,δa)，然后将飞行器输出量输入到机翼关键部件载荷应力分析中得到其关键部件受到的动态载荷量，最后将该动态载荷量作为损伤动力学模型的输入量，得到机翼关键部件的损伤动态特性。本文将针对飞行器进行高超声速飞行的特定任务区间，模拟翼梁根部损伤的演化过程。

为了定性分析飞行器各个变量对损伤演化的影响，在仿真中不考虑各个变量间的相互耦合作用。同时为了模拟翼梁根部受到的循环载荷作用，在飞行器气动系数中加入频率为2 Hz,幅度为5%的时变不确定。另外，根据已有的高超声速飞行器结构材料和气动热的研究成果可知机翼翼梁材料可选用镍基合金Haynes230[13]，而机翼表面由于有隔热层保护使得翼梁结构温度最高不会超过500 ℃[14]。根据Haynes230合金材料手册可知该合金在800 ℃内力学性能较稳定[15]，本文中翼梁材料参数采用的是其约在450 ℃下的材料参数，其拉伸屈服应力和极限应力分别为：σyield=283 Mpa，σuts=522 Mpa;材料Paris常数约为：C=0.85×10-18，m=2.08;结构几何常数w=0.5δ1=3×10-2;衰减系数η=δ2σyield/δ1E=4.8×10-3;材料杨氏模量E=195 GPa;约束因子ε=2.1。飞行器总质量恒定为M=136 820 kg，机翼相关结构尺寸分别为：Sw=167.36 m2,c=24.38 m,b=18.29 m,l0=3.048 m,δ1=0.06 m,δ2=0.20 m;对应编号翼梁高度H1=H4=0.480 m,H2=H3=0.695 m;对应编号翼梁截面积A1=A4=0.046 m2,A2=A3=0.058 m2,Mw=2500 kg。

设初始裂纹长度a0=0.1 mm；设计飞行器任务区间高度范围为30 km≤H≤35 km，任务区间马赫数范围7～10，限制飞行器迎角范围为-4°≤α≤10°，舵面偏转角度范围-30°≤δe≤30°，根据以上的仿真参数，分别对高超声速飞行器在高度、速度、迎角、舵面偏角变化时翼梁根部的损伤演化情况进行仿真，如下所示。

1) 仅速度V变化时损伤演化情况。

设置δe=0°，H=30 km，α=2°，μ=0°，马赫数依次设为7,8.5,10，得到的裂纹在100 s内的演化趋势情况如图3a、图3b所示。

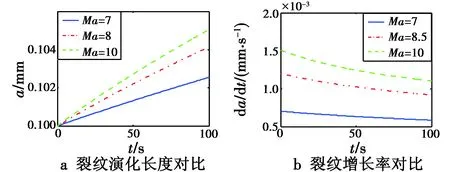
图3 仅马赫数变化时裂纹演化情况对比Fig.3 Crack evolution contrast with only Ma changed

从图3可以看出，在H,α,δe,μ均固定的情况下，速度V越大，裂纹增长的速率越大。原因主要是速度越大，机翼受到的升力Lw和阻力Dw越大，使得翼梁根部受到的载荷应力也越大，因此导致翼梁根部的细微裂纹增长得也越快。从图3a可得到在t=100 s时刻，Ma=7对应裂纹长度约为0.102 5 mm，增幅为2.5%；Ma=8.5对应裂纹长度约为0.104 1 mm，增幅为4.1%；Ma=10对应裂纹长度约为0.105 1 mm，增幅为5.1%。

2) 仅迎角α变化时损伤演化情况。

设置δe=0°，H=30 km，马赫数为7，μ=0°，迎角依次设为-4°,-2°,2°,6°,10°，得到的裂纹在100 s内的演化趋势情况如图4所示。

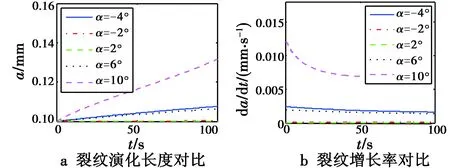
图4 仅迎角α变化时裂纹演化情况对比Fig.4 Crack evolution contrast with only α changed

从图4可以看出，在H,V,δe,μ均固定的情况下，迎角α越大，裂纹损伤的增长速率越大。主要原因是在允许迎角范围内，随着α绝对值的增加，机翼的升阻力系数CL,CD逐渐变大，使得Lw,Dw越大，因此翼梁根部受到的载荷应力也越大。从图4a可得出在t=100 s时刻:α=-4°对应裂纹长度约为0.108 7 mm，增幅约为8.7%；α=-2°对应裂纹长度约为0.100 9 mm，增幅为0.9%；α=2°对应裂纹长度约为0.101 5 mm，增幅为1.5%；α=6°对应裂纹长度约为0.108 7 mm，增幅为8.7%；α=10°对应裂纹长度约为0.132 8 mm，增幅为32.8%。

3) 仅高度H变化时损伤演化情况。

设置δe=0°，马赫数为7，α=2°，μ=0°，高度H依次设为30 km,33 km,35 km，得到的裂纹在100 s内的演化趋势情况如图5所示。

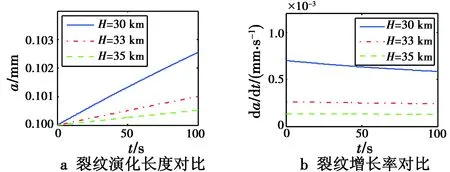
图5 仅高度H变化时裂纹演化情况对比Fig.5 Crack evolution contrast with only H changed

从图5可以看出，在V,α,δe,μ均固定的情况下，高度H越大，裂纹的增长速率越小。主要原因是随着高度的增加，大气密度逐渐下降，使得Lw,Dw逐渐减小，从而使得翼梁根部受到的载荷应力变小。从图5a可以得到,在t=100 s时刻，H=30 km对应裂纹长度约为0.102 5 mm，增幅为2.5%；H=33 km对应裂纹长度约为0.101 1 mm，增幅为1.1%；H=35 km对应裂纹长度约为0.100 6 mm，增幅为0.6%。

4) 仅副翼偏转角δe变化时损伤演化情况。

设置H=30 km，马赫数为7，α=2°，μ=0°，副翼偏转角δe依次设为-30°,-15°,0°,15°,30°，得到的裂纹在100 s内的演化趋势情况如图6所示。

图6 仅副翼偏角δe变化时裂纹演化情况对比Fig.6 Crack evolution contrast with only δe changed

从图6可以看出，在H,V,α,μ均固定的情况下，副翼偏转角度δe越大，裂纹的增长速率越大。主要原因是，随着δe绝对值的增加，机翼的升阻力系数CL,CD逐渐变大，机翼受到的Lw,Dw越大，因此翼梁根部受到的载荷应力也越大。从图6a可得到在t=100 s时刻:δe=-30°对应裂纹长度约为0.103 9 mm，增幅约为3.9%；δe=-15°对应裂纹长度约为0.102 1 mm，增幅约为2.1%；δe=0°对应裂纹长度约为0.101 3 mm，增幅约为1.3%；δe=15°对应裂纹长度约为0.101 8 mm，增幅约为1.8%；δe=30°对应裂纹长度约为0.103 3 mm，增幅约为3.3%。

另外，由于滚转角μ对机翼的载荷应力的影响等效于副翼偏转角δe对机翼的载荷应力的影响，因此本文不再对μ进行单独分析。

从以上飞行器各变量对翼梁根部损伤的分析数据可以看出，在限定各变量变化范围的前提下，迎角α增大对翼梁根部的损伤影响是最大的，明显大于H,V,δe变化所对应的损伤增长率。速度V对翼梁根部裂纹演化的影响程度稍大于高度H和副翼偏转角δe对翼梁根部裂纹演化的影响。

从结构安全容限角度来看，本文中所选取翼梁腹板、缘条厚度δ1=6 cm，为翼梁结构中尺寸最小部分，若规定结构最小尺寸的1%为容许裂纹损伤的临界值，即临界裂纹长度为0.6 mm。依照本文中的仿真数据，当存在初始裂纹长度为0.1 mm时，飞行器在100 s内进行正常的机动是安全可靠的，但是从保证飞行器飞行绝对安全与延长使用寿命的角度来看，当飞行器在做高超声速飞行时，应该限制飞行迎角大小。

5 结束语

本文在建立了高超声速飞行器机翼关键部件损伤动力学模型、飞行器动力学模型以及对机翼关键部件载荷应力分析的基础上，分别分析了速度、高度、迎角以及舵面偏角对翼梁根部损伤特性的影响。分析结果表明，飞行迎角对翼梁根部的损伤影响最大，而速度、高度以及舵面偏角对其影响相对较小。通过对翼梁根部损伤的影响因素与动态特性进行定性分析，可以为延寿控制设计与飞行器结构可靠性设计提供有价值的参考依据。

[1] 叶友达.近空间高速飞行器气动特性研究与布局设计优化[J].力学进展,2009,39(6)：683-694.

[2] FIORENTINI L,SERRANI A.Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model[J].Automatica,2012,48(7):1248-1261.

[3] 王宏伦,邵星灵,张惠平,等.面向大跨度机动飞行的高超声速飞行器自抗扰轨迹线性化控制[J].电光与控制,2015,22(12)：1-8.

[4] 高宗战,刘志群,姜志峰.飞机翼梁结构强度可靠性灵敏度分析[J].机械工程学报,2010,46(14)：194-198.

[5] 张永芳,刘旭,冯雪,等.机翼结构件的疲劳测试[J].交通运输工程学报,2012,12(6)：55-62.

[6] 孟凡涛,胡愉愉.基于频域法的随机振动载荷下飞机结构疲劳分析[J].南京航空航天大学学报,2012,44(1):32-36.

[7] TRENDAFILOVA I,CARTMELL M P,OSTACHOWICZ W.Vibration-based damage detection in an aircraft wing scaled model using principal component analysis and pattern recognition[J].Journal of Sound and Vibration,2008,313(3):560-566.

[8] 翟新康,黄其新,殷之平,等.飞机整体翼梁结构裂纹扩展试验与分析[J].机械强度,2007,29(6)：987-991.

[9] 黄其新,刘进征,殷之平.整体翼梁结构断裂特性分析方法与研究[J].航空计算技术,2006,36(2)：114-119.

[10] 李曙林,李寿安.某型飞机机翼Ⅱ梁框疲劳寿命研究[J].机械科学与技术,2005,24(6)：686-688.

[11] CAPLIN J,RAY A,JOSHI S M.Damage-mitigating control of aircraft for enhanced structural durability[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(3):849-862.

[12] 吴永瑞,邓宗白,周克印,等.材料力学[M].北京:高等教育出版社,2011.

[13] 郭朝邦,李文杰.高超声速飞行器结构材料与热防护系统[J].飞航导弹,2010(4):88-94.

[14] GLASS D E.Ceramic Matrix Composite (CMC) Thermal Protection Systems (TPS) and hot structures for hypersonic vehicles[C]//The 15th AIAA Space Planes and Hypersonic Systems and Technologies Conference,2008:1-36.

[15] Haynes International.Haynes230 alloy brochure:No.H-3000[EB/OL].(2010-08-26)[2016-07-26].http://haynesintl.com/docs/default-source/pdfs/new-alloy-brochures/high-temperature-alloys/brochures.

DamageCharacteristicAnalysisofKeyComponentsofHypersonicAircraftWing

SHAO Peng1, WANG Yu-hui1,2, WU Qing-xian1, ZHEN Wu-bin1

(1.College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China; 2.Science and Technology on Electro-Optic Control Laboratory,Luoyang 471000,China)

Analysis is made to the damage evolution of the key component of hypersonic aircraft wing and the influence of flight dynamics on the damage.Based on establishment of damage dynamic model of the key components of hypersonic aircraft wing and dynamic model of hypersonic aircraft,and the loading stress analysis of the key components of wing,the effects of flight altitude,air speed,angle of attack and deflection of control surfaces on the dynamic damage characteristics of the key components of wing are studied respectively,thus to confirm the key aircraft variables having significant influence on the damage.The results show that the angle of attack has the most significant influence on the damage evolution of the key components of wing.From the safety and life extending perspectives,the angle of attack should be kept within a strict range while the aircraft is flying at hypersonic speed.The results can provide a valuable reference for the design of structure reliability.

hypersonic aircraft; wing; damage dynamic model; dynamic damage characteristic

邵鹏,王玉惠,吴庆宪,等.高超声速飞行器机翼关键部件损伤特性分析[J].电光与控制，2017，24(7)：70-74,80.SHAO P,WANG Y H,WU Q X,et al.Damage characteristic analysis of the key components of hypersonic aircraft wing[J].Electronics Optics & Control,2017,24(7):70-74,80.

V271.4; TP273

A

10.3969/j.issn.1671-637X.2017.07.015

2016-07-26

2016-08-16

中央高校基本科研业务费项目(NS2015031);国家自然科学基金(61374212);航空科学基金(20135152047)

邵 鹏(1991 —),男，云南德宏人，硕士生，研究方向为高超声速飞行器减损控制。态的不断变化，机体与大气相互作用产生复杂的气动干扰，使得机翼表面存在非常复杂的气动载荷分布[1-3]。机翼翼梁根部位置不仅需要承受飞行器自身的重力，还要承受机翼在超高速气流中受到的巨大的气动载荷所带来的载荷应力作用，因此翼梁根部作为机翼的关键部件出现疲劳损伤的概率是最大的，翼梁根部的安全也极大地影响着飞行安全[4]。因此，对高超声速飞行器机翼关键部件的损伤特性研究具有重要的意义。