基于小波降噪和盲源分离算法的信号分离方法研究

王川川， 曾勇虎， 赵明洋， 汪连栋

(电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003)

基于小波降噪和盲源分离算法的信号分离方法研究

王川川， 曾勇虎， 赵明洋， 汪连栋

(电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳471003)

针对含噪情况下的盲源分离问题，将小波降噪方法引入盲源分离模型之中，对两种小波降噪与盲源分离算法结合的信号分离方法，即预降噪+盲源分离，以及预降噪+盲源分离+后降噪，从理论上进行了原理与特点分析，并通过数值仿真比较了不同信噪比情况下两种方法对于混合信号的分离效果。仿真表明，采用小波降噪与盲源分离结合的信号分离方法，相比于单纯采用盲源分离算法，能够大大提高信号的分离效果;预降噪+盲源分离+后降噪的信号分离方法比采用预降噪+盲源分离的信号分离方法效果普遍提高。

小波降噪； 盲源分离； 自然梯度法； 等变自适应分解； 相似系数

0 引言

盲源分离算法是信号处理领域的一个研究热点。由于盲信号处理中存在许多的未知条件，对带噪声的混叠信号进行分离是困难的，通常假定无噪声或把噪声看作一个独立源信号。虽然某些算法采用了特征值分解等线性代数的子空间理论，具备一定的噪声抑制为提高盲源分离算法的稳定性及应用效果，学者们针对待分离信号中叠加的加性噪声，提出了多种预处理方法。由于许多实际信号，如雷达、通信信号等，都是典型的非平稳信号，经典的基于傅里叶变换的滤波方法不再有效[3]。小波变换具有良好的时、频局部化性质和多分辨率分析的特点，近年来已被逐渐用于信号去噪领域且取得良好的效果。文献[1]应用小波分析和经验模态分解(EMD)方法对含噪信号进行预降噪，再进行信号的盲分离操作;文献[2]针对含噪环境下的盲源分离问题，将一种稳健的含噪条件下的白化预处理方法应用于FastICA算法中;文献[4-5]的处理思路是首先利用小波滤波器对测试信号进行消噪处理，再进行信号的分离操作。文献[6-7]针对含噪声混合信号分离问题，提出了首先采用小波滤波进行去噪处理，再进行信号的盲源分离操作，最后对分离后的信号二次使用小波滤波处理的信号分离思路。

综合分析发现，文献中对含噪信号进行盲源分离操作的绝大多数方法可归纳为两类:一是预降噪+盲源分离;二是预降噪+盲源分离+后降噪。为获得盲源分离算法最佳的应用效果，本文对文献中两种处理方法的原理进行了分析比较，通过仿真算例具体比较了不同信噪比情况下信号的分离效果。

1 含噪信号盲源分离模型

n部辐射源的发射信号可以表示为s(t)=(s1(t)s2(t) …sn(t))T∈Rn×T0，T0表示信号采样点数，n个源信号在传播及接收过程中，势必会产生信号混叠，由接收阵列接收的混合信号表示为x(t)=(x1(t)x2(t) …xm(t))T∈Rm×T0，m为接收天线个数。

含噪盲源分离数学模型可表示为

x(t)=As(t)+n(t)t=1,2,…,T0

(1)

式中,n(t)=(n1(t)n2(t) …nm(t))T∈Rm×T0,表示接收信号中叠加的m个加性噪声。噪声的存在，使得观测信号信噪比降低，盲源分离算法应用效果严重降低。

2 小波降噪和盲源分离算法的联合应用方法

2.1 小波降噪方法基本原理

基于小波分析的去噪方法主要有基于模极大值去噪法、小波阈值去噪法和平移不变量去噪法。其中，小波阈值去噪方法[8]在Besov空间上可得到最佳估计值，而任何其他线性估计都达不到同样的估计结果，因此引起了世界范围内学者的广泛关注。本文选择小波阈值去噪法对含噪信号进行消噪。

在生产中，做好生产配合比的设计，保证目标配合比在拌和中得以实现是关键。首先从热料仓供料抓起，采取措施保证各仓均衡储料；保证原料组成的稳定和供料比例。然后要做好对拌和温度及拌和时间的控制，保证沥青、集料及混合料拌和、储存、出场温度。

设一个带噪信号为

x(i)=s(i)+n(i)

(2)

式中：x(i)为含噪信号；s(i)为有用信号;n(i)为噪声;i=0,1,…,N-1。

小波阈值法去噪的基本步骤如下[8-9]所述。

1) 选择合适的小波基。DbN,symN和CoifN是最常用的小波基。其中，Db系列小波基因为其在正交性、紧支撑性、支撑长度等方面都优于其他小波基，所以常被选择对含噪信号进行分析。

2) 选择合适的分解层数J，利用式(3)对信号进行正交小波变换，得到各层的尺度系数cj,k和小波系数dj,k，算法初值为x(i)=c0,k。

(3)

式中:k=0,1,…,N-1，N为信号采样点数;j=0,1,…,J，J为分解层数；h和g互为正交滤波器组。

文献[6-7]指出，一般分解层数选择3层即可大大提高降噪效果。

4) 根据式(4)，对信号进行重构，得到降噪处理后的信号，即

(4)

2.2 预降噪+盲源分离的信号分离方法

盲源分离算法对于信号中叠加的加性噪声极为敏感，如基于最大信噪比准则的盲源分离算法要求信号具备较高信噪比的条件。为提高盲源分离算法的稳定性和分离效果，一个自然的选择就是首先对信号进行预降噪，然后进行信号分离工作。这种分离方法的基本原理如图1所示。

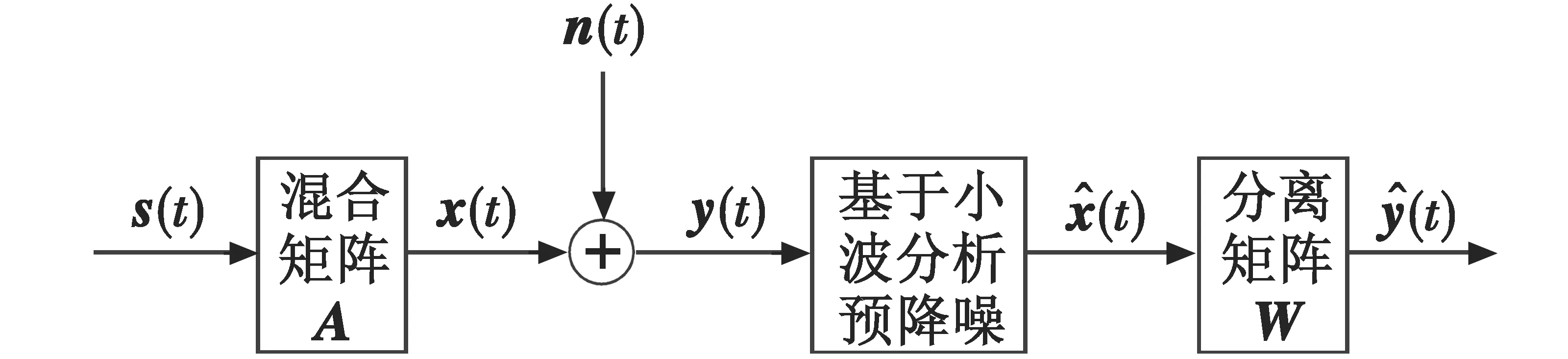
图1 预降噪+盲源分离的信号分离方法框图Fig.1 Block diagram of pre-denoising+blind source separation algorithm

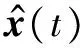
2.3 预降噪+盲源分离+后降噪的信号分离方法

学者们提出的另一种降噪算法和盲源分离算法结合的信号分离方法原理如图2所示。

图2 预降噪+盲源分离+后降噪的信号分离方法框图Fig.2 Block diagram of pre-denoising+blind source separation algorithm+post-denoising

应用图2所示方法，从理论上讲，不仅可以通过预降噪提高盲源分离算法的稳定性，还可以通过后降噪处理进一步提高分离信号的信噪比，使得分离效果得到提高。这种方法同2.2节方法一样，应用的关键都在于预降噪中小波分解尺度的选择，若分解尺度过大，将使得混合信号严重失真，混合矩阵A和源信号s都产生严重失真，因此,尽管可以估计得到混合矩阵并分离得到源信号，最终信号分离效果也不会好。图1和图2所示方法若要达到较好的效果，必须对观测信号中叠加噪声的方差进行估计，而这是小波降噪算法的一个技术难点，目前学者们对此研究还很不足，导致小波降噪算法的应用仍具有一定的随意性。

3 仿真实验与分析

为了对第2章中的两种信号分离思路进行评估，对以下典型信号进行了混叠及分离仿真实验。

1) 符号信号：

s1(t)=sgn[cos(2π·155·t/fs)]；

2) 高频正弦信号：

s2(t)=sin(2π·800/fs)；

3) 幅值调制信号：

混合信号中叠加噪声为高斯白噪声。本文应用小波阈值降噪方法对信号进行降噪，小波基函数选择小波阈值降噪中应用较多、效果普遍较好的Db9小波，第一、第二种分离思路中小波分解层数为3层。阈值估计方法选用启发式阈值，阈值函数选用软阈值函数。应用两种盲源分离算法对信号进行分离，这两种盲源分离算法是基于等变自适应分解的盲源分离算法(Equivariant Adaptive Source Separation via Independence,EASI)[10]和基于自然梯度法(Natural Gradient,NG)的盲源分离算法[11]。应用相似系数来评价分离结果的准确性。

含噪混叠信号在不同信噪比情况下，分别应用EASI信号分离方法，小波预降噪+EASI的信号分离方法(WL+EASI)，以及小波预降噪+EASI+小波后降噪的信号分离方法(WL+EASI+WL)，对上述混合信号进行分离操作，计算得到的分离信号与源信号相似系数矩阵如表1所示，其中，采用WL+EASI+WL的分离方法时，计算相似系数矩阵采用的是最终降噪后的分离信号。在SNR为13.6 dB的情况下，3种方法对应的部分仿真波形如图3所示。

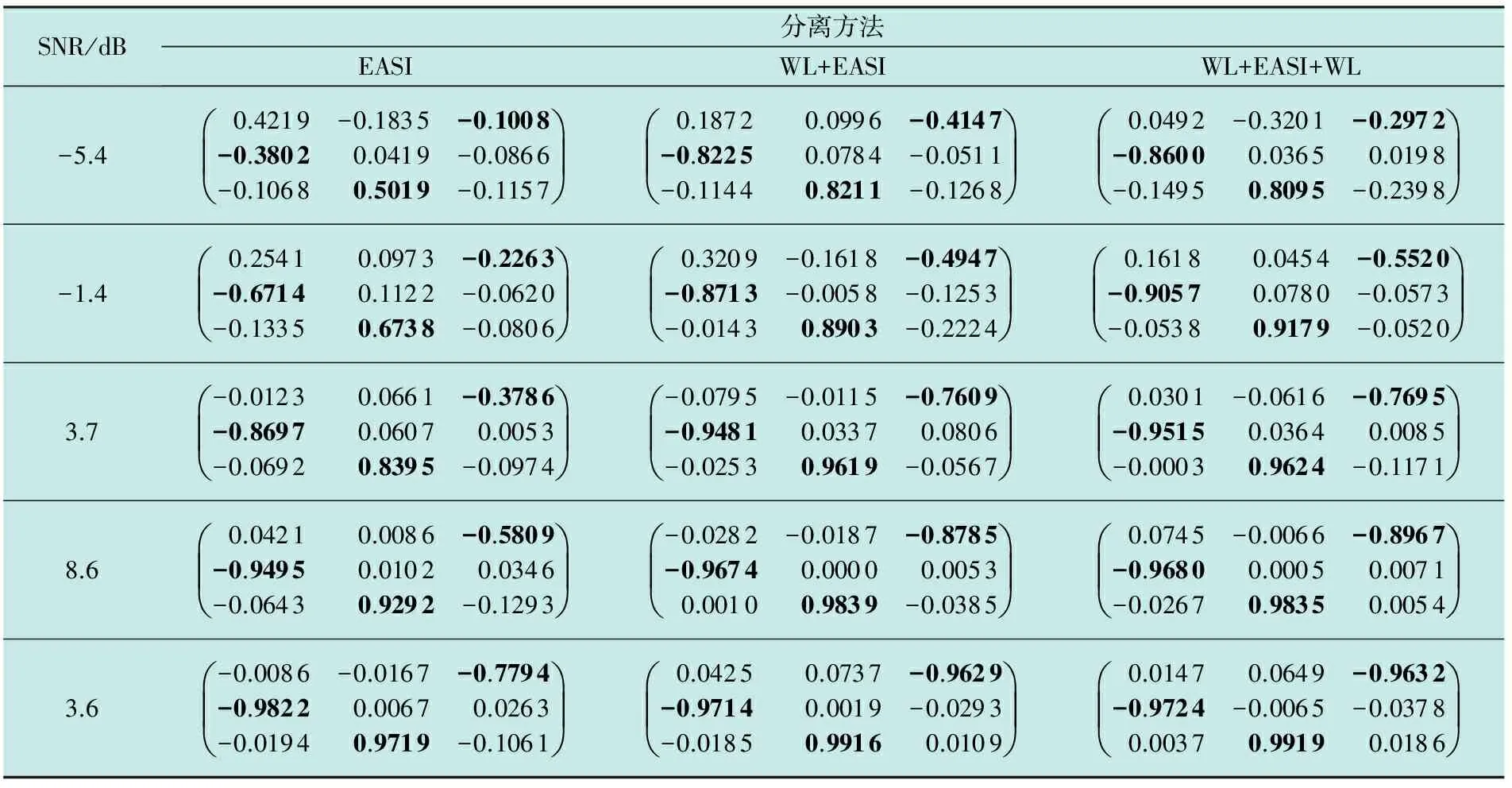
表1 3种方法分离信号与源信号的相似系数

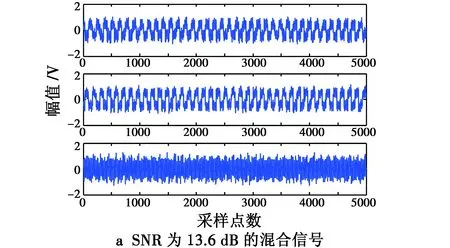
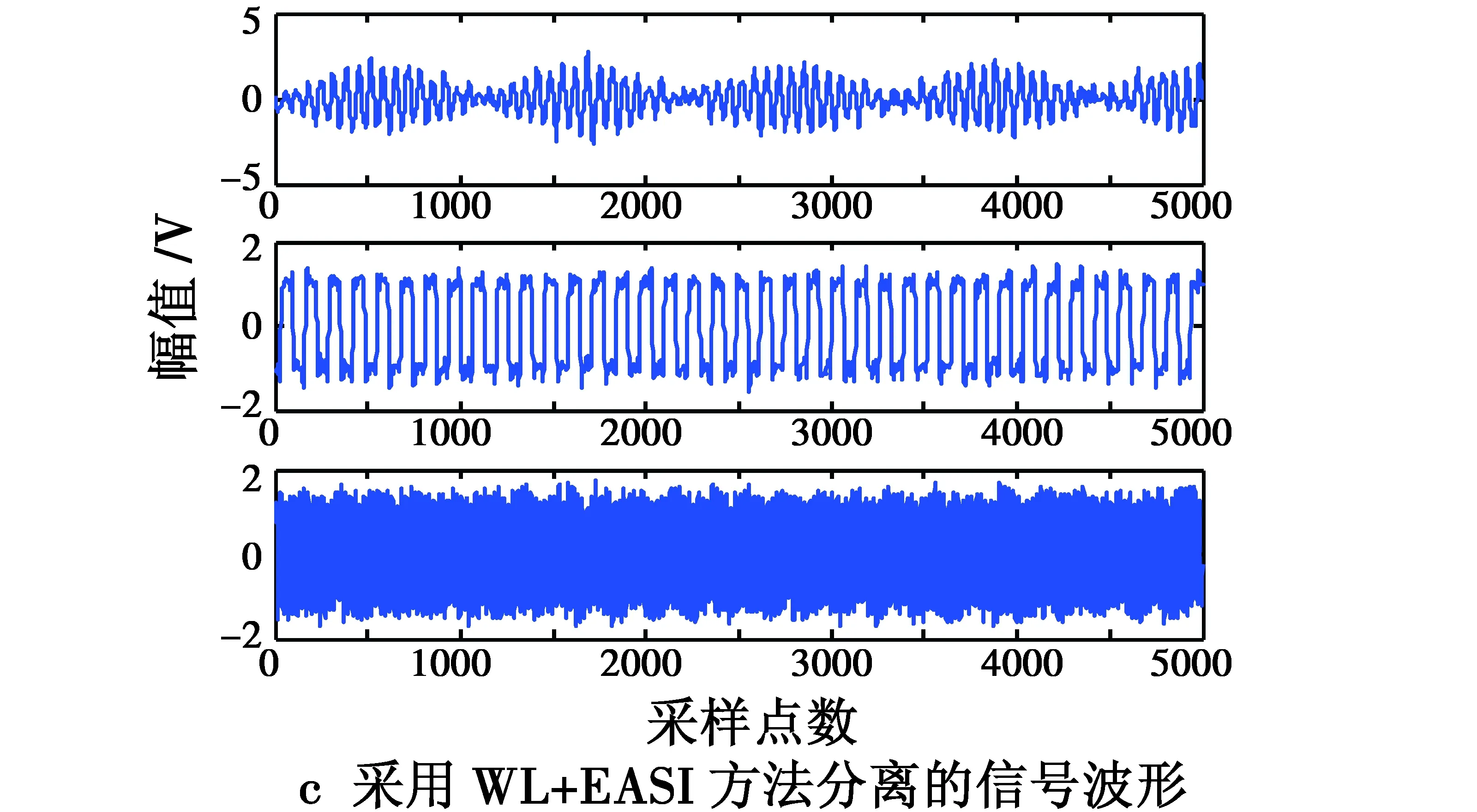
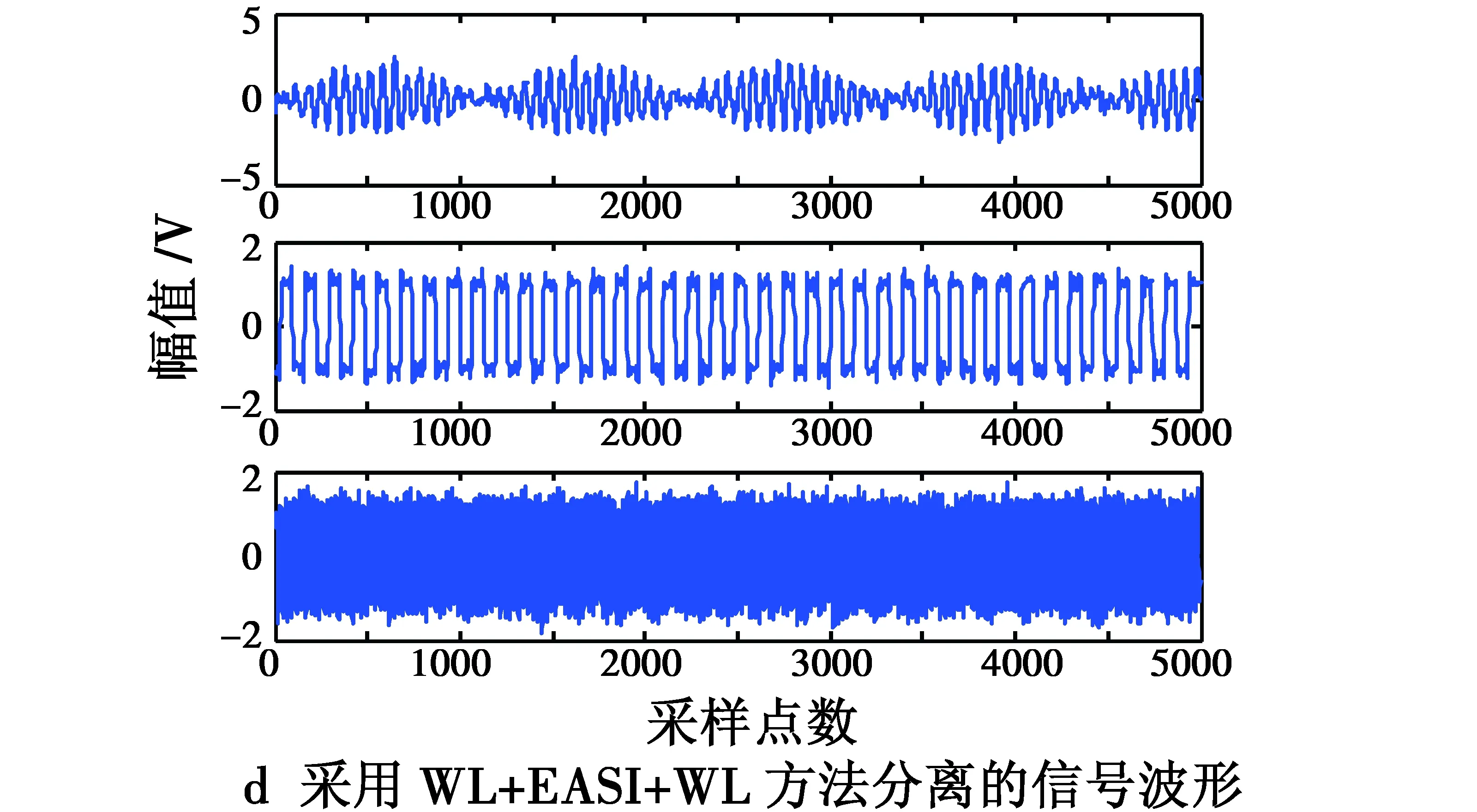
图3 源信号、混合信号和分离信号波形Fig.3 Waveforms of source signal,mixed signals and separated signals

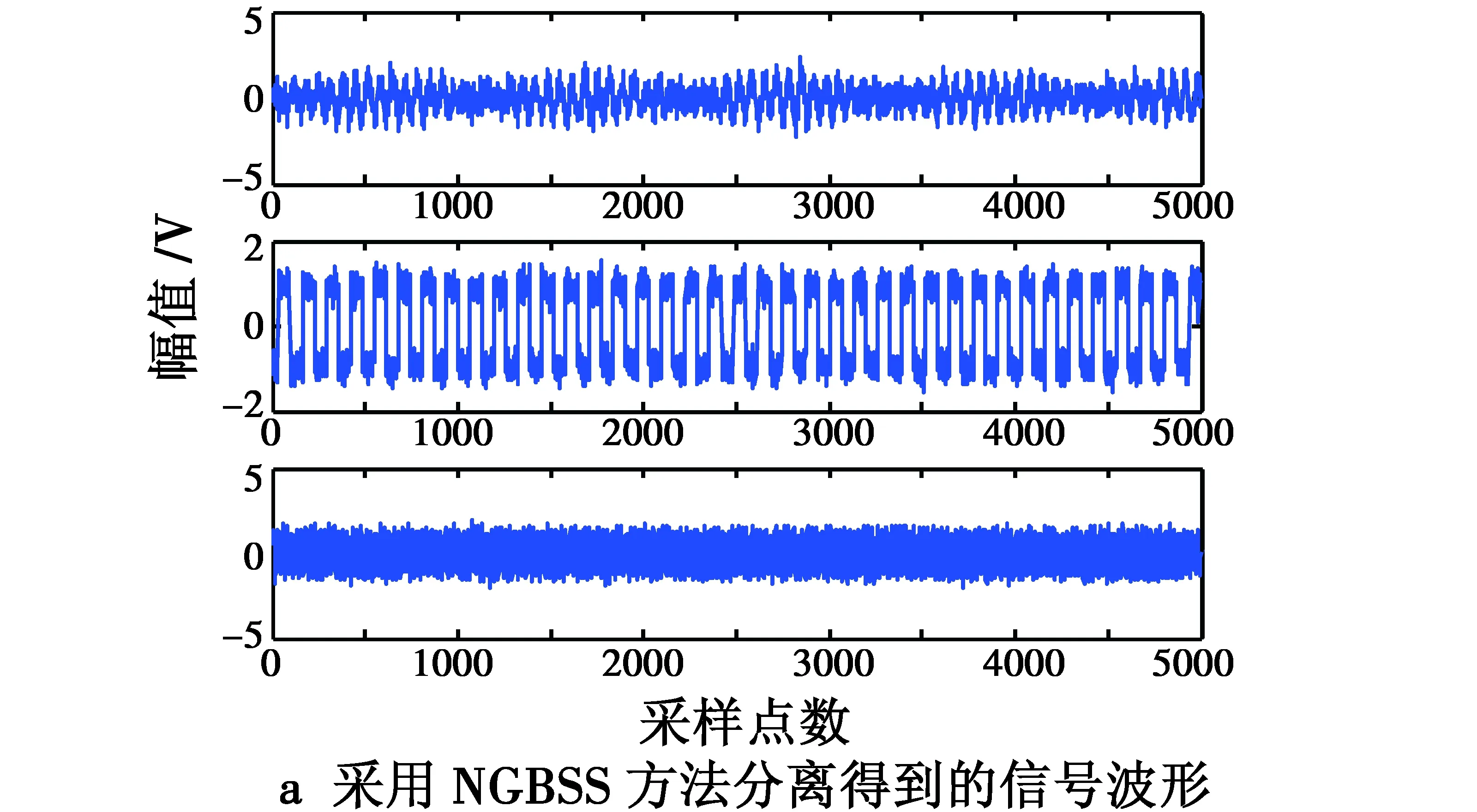
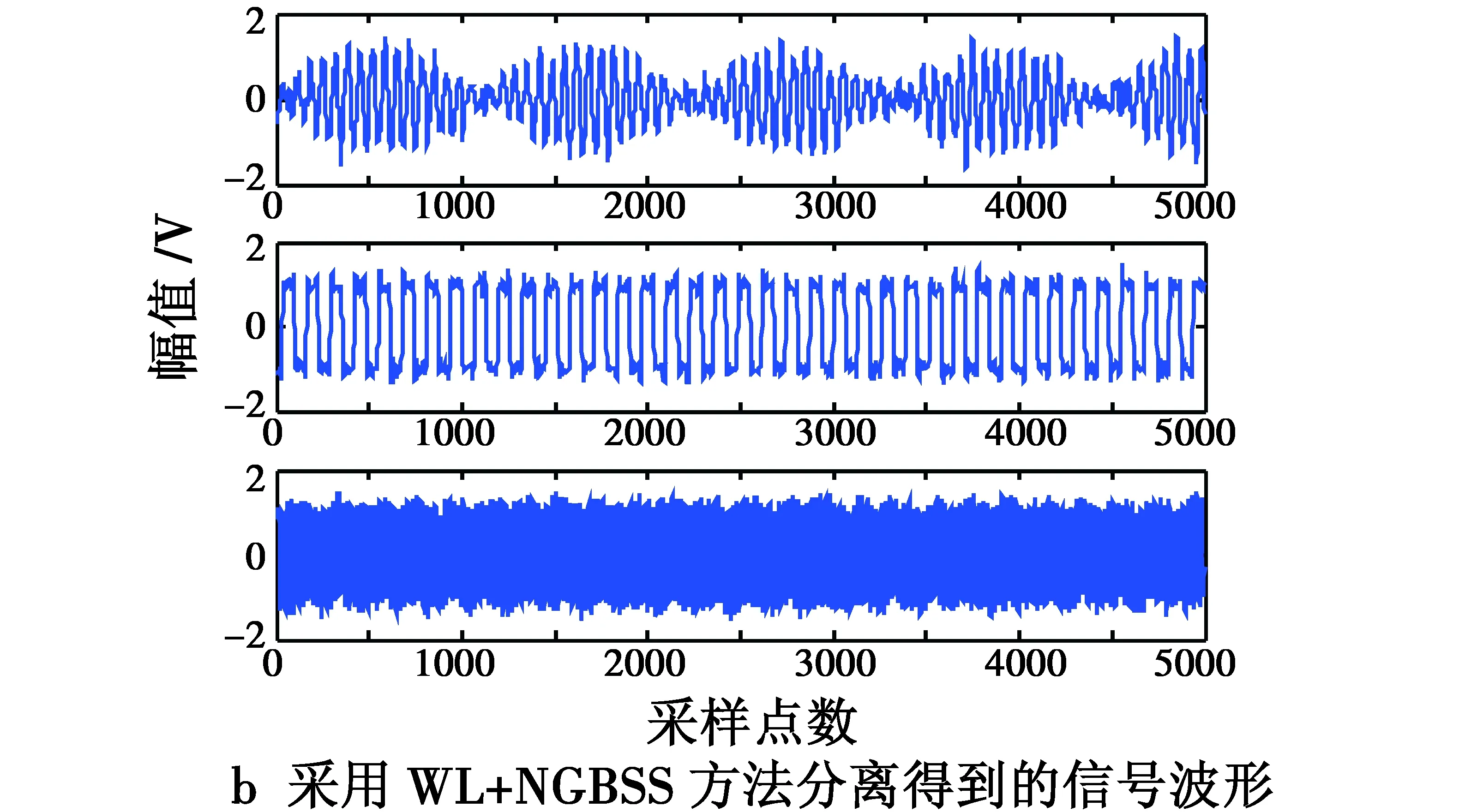
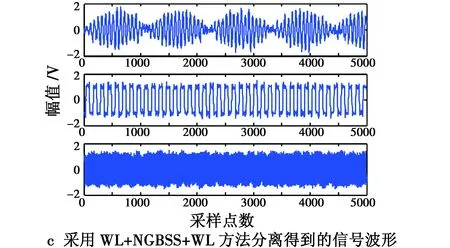
图4 不同方法得到的分离信号Fig.4 Separated signals obtained by different separation methods

对混合信号叠加噪声，分别应用基于自然梯度法的盲源分离算法、小波预降噪+NG的信号分离方法(WL+NGBSS)，以及小波预降噪+NGBSS+小波后降噪的信号分离方法(WL+NGBSS+WL)，对上述混合信号进行分离操作，计算得到的分离信号与源信号相似系数矩阵如表2所示，其中，采用WL+NGBSS+WL的分离方法时，计算相似系数矩阵采用的是最终降噪后的分离信号。 在SNR为13.6 dB的情况下，3种方法对应的部分仿真波形如图4所示。 从表1可看出，在混合信号信噪比为-5.4 dB时，直接应用盲源分离算法，计算得到的分离信号与源信号最大相似度分别只有-0.380 2,0.501 9,-0.100 8，这表明没有一个信号被正确分离，采用预降噪+EASI方法，最大相似度分别为-0.822 5,0.821 1,-0.414 7，采用预降噪+EASI+后降噪方法，最大相似度分别为-0.860 0,0.809 5,-0.297 2。在表2中，当混合信号信噪比为-5.4 dB时，采用3种方法，分离信号与源信号的相似度趋势与表1中相同。由此可见，采用预降噪+盲源分离，以及预降噪+盲源分离+后降噪的信号分离方法，都成功分离出两个信号，使得在低信噪比情况下成功分离信号的数量获得提高。综合分析表1和表2可发现：相比于不对混合信号采用降噪处理的信号分离方法，采用预降噪+盲源分离，以及预降噪+盲源分离+后降噪的信号分离方法，在混叠信号信噪比变化的情况下，分离得到的信号与源信号相似度普遍获得提高。从图3和图4可看出，采用后两种方法分离得到的信号波形更加纯净。以上分析表明，在信号分离操作中加入降噪处理环节，将大大提高信号分离效果。

基于分离信号与源信号相似度计算结果，比较预降噪+盲源分离的信号分离方法与预降噪+盲源分离+后降噪的分离方法，发现后者普遍使得分离效果得以改善。

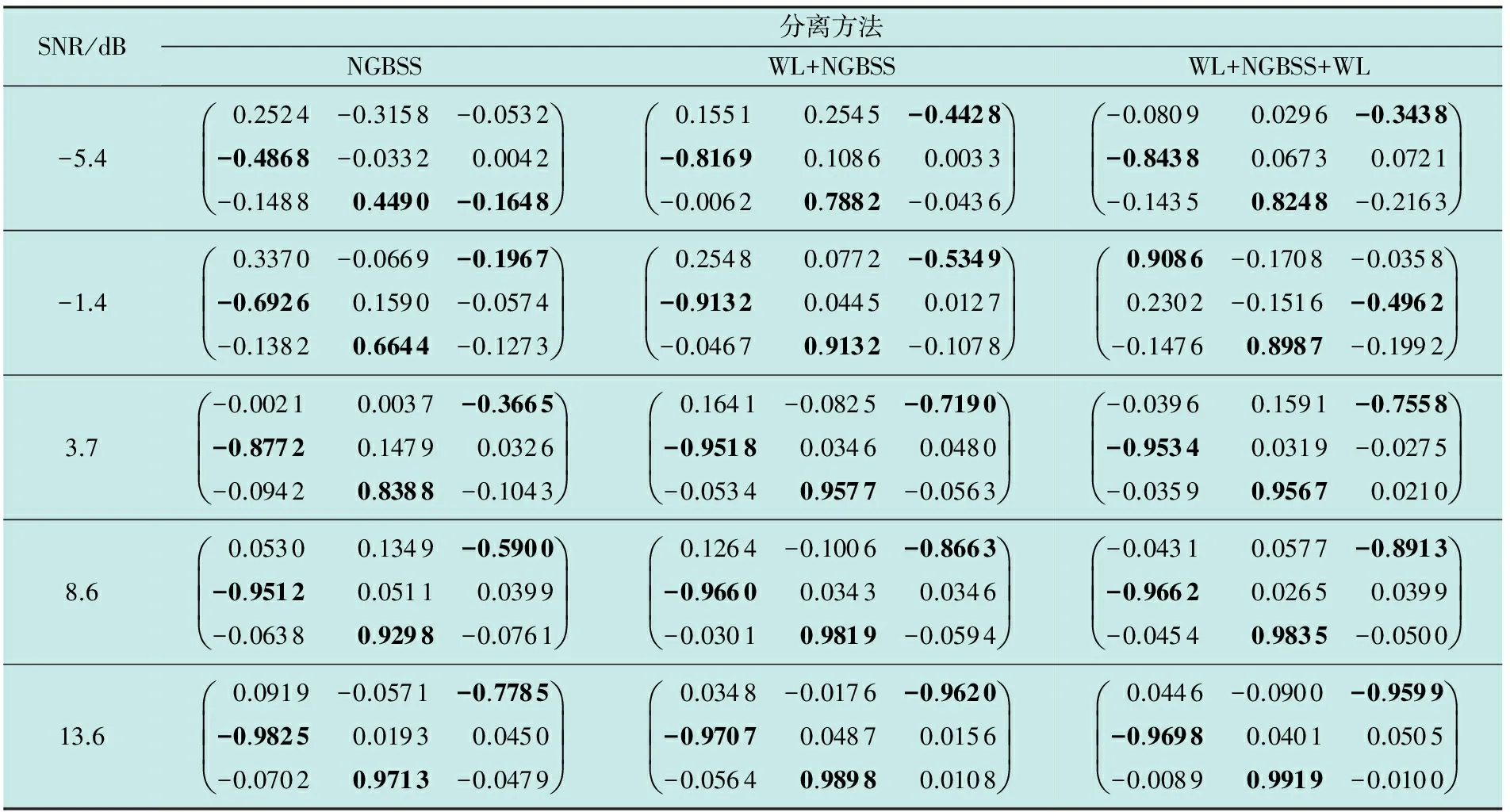
表2 3种方法分离信号与源信号的相似系数

4 结论

为改善盲源分离算法的应用效果，本文对两种小波降噪与盲源分离算法结合的信号分离方法，即预降噪+盲源分离及预降噪+盲源分离+后降噪进行了原理与特点分析，并以基于等变自适应分解(EASI)以及基于自然梯度法(NG)的盲源分离算法为例，通过数值计算比较了不同信噪比情况下信号的分离效果。仿真表明，采用预降噪+盲源分离的信号分离方法，以及预降噪+盲源分离+后降噪的信号分离方法，相比于单纯采用盲源分离算法，使得信号的分离效果普遍获得提高，改善了盲源分离算法在低信噪比情况下应用的稳定性，且后一种方法分离效果相比前一种方法普遍有所提高。

[1] 王尔馥.盲源分离理论及其在通信系统中的应用[D].哈尔滨:哈尔滨工业大学,2009.

[2] 吴微,彭华,周正康.一种改进的FastICA算法及其在含噪盲源分离中的应用[J].信息工程大学学报,2013,14(6):708-712.[3] 张晗博,殷奕,殷奎喜.基于小波变换的非平稳信号分析与处理[J].南京师范大学学报,2014,14(1):63-69.

[4] 孟宗,马钊,刘东,等.基于小波半软阈值消噪的盲源分离方法[J].中国机械工程,2016,27(3):337-342.

[5] 蔡伟华,何选森.基于UWT和独立分量分析的含噪盲源分离[J].计算机工程与应用,2016,52(16):180-185.

[6] 赵奎,黄高明.基于二次小波去噪的FastICA盲源分离研究[J].舰船电子工程,2015,35(6):36-40.

[7] 王杏.带噪混叠语音信号盲分离方法研究[D].北京:北京交通大学,2014.

[8] 孔玲军.MATLAB小波分析超级学习手册[M].北京:人民邮电出版社,2014.

[9] DONOHO D L.Denoising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.

[10] CARDOSO J F,LAHELD B H.Equivariant adaptive source separation[J].IEEE Transactions on Signal Processing, 1996,44(12):3017-3030.

[11] AMARI S L.Natural gradient learning for over-and under-complete bases in ICA[J].Neural Computation,1999,11(8):1875-1883.

SignalSeparationMethodBasedonWaveletDe-noisingAlgorithmandBlindSourceSeparationAlgorithm

WANG Chuan-chuan, ZENG Yong-hu, ZHAO Ming-yang, WANG Lian-dong

(State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System,Luoyang 471003,China)

Aiming at the problem of blind source separation in noisy environment,wavelet de-noising method is introduced into blind source separation model.Two separation methods,pre-denoising+blind source separation algorithm,and pre-denoising+blind source separation algorithm+post-denoising,are analyzed theoretically.Then,comparison is made to the separation results of the two methods through digital simulation.The simulation shows that:1) Compared with the method only using blind source separation algorithm,the separation method combining wavelet de-noising with blind source separation algorithm has much better separation effect; and 2) The separation effect of pre-denoising+blind source separation algorithm+post-denoising is generally better than that of pre-denoising+blind source separation algorithm.

wavelet denoising; blind source separation; natural gradient method; equivariant adaptive source separation; similarity coefficient

王川川,曾勇虎,赵明洋,等.基于小波降噪和盲源分离算法的信号分离方法研究[J].电光与控制，2017，24(7)：7-11.WANG C C,ZENG Y H,ZHAO M Y,et al.Signal separation method based on wavelet de-noising algorithm and blind source separation algorithm[J].Electronics Optics & Control,2017,24(7):7-11.

TN911.4

A

10.3969/j.issn.1671-637X.2017.07.002

2016-06-02

2016-07-21

国家自然科学基金(61372040)；CEMEE国家重点实验室开放课题(CEMEE2015Z0302B)

王川川(1985 —),男，河南濮阳人，博士，助理研究员，研究方向为电子信息系统效能评估理论。能力，但还十分有限。文献[1-2]研究了噪声对分离矩阵估计的影响，表明加性噪声导致信号分离精度严重下降。