基于改进ADRC的巡飞弹纵向控制系统研究

黄 瑞， 陈建辉， 高 敏， 陶贵明

(军械工程学院，石家庄 050003)

基于改进ADRC的巡飞弹纵向控制系统研究

黄 瑞， 陈建辉， 高 敏， 陶贵明

(军械工程学院，石家庄 050003)

针对近程巡飞弹纵向控制系统设计中存在系统模型的非线性、不确定性、耦合性等问题，引入了自抗扰控制(ADRC)方法。介绍了ADRC的结构、原理、算法实现及参数整定规则，设计具有解耦抗干扰能力的ADRC。针对扩张状态观测器线性区间宽度参数较小时出现的震颤现象和控制性能降低的问题，提出了一种改进非线性函数的方法，设计了纵向运动控制系统。在Simulink平台下进行仿真实验，仿真结果表明，提出的改进方法有效解决了震颤问题，增强了控制器性能，设计的改进自抗扰纵向巡飞控制系统具有良好的控制性能，验证了该改进方法及控制系统的合理性。

自抗扰控制； 姿态控制； 巡飞弹； Simulink； 抗干扰

0 引言

近程巡飞弹是无人机技术和精确制导弹药技术有机结合的产物，可实现巡飞侦察、毁伤评估、精确打击、通信中继、目标指示、空中警戒等作战功能[1]。

近程巡飞弹由于其结构简单、携带方便、机动性能好、效费比高，被广泛应用于战场监视、侦察，时间敏感目标打击、反恐特战等重要领域，在现代战争中的作用越来越突出，是目前国际上先进武器装备不可或缺的

由于巡飞弹是近几年提出的新概念新武器，对其巡飞控制系统设计的研究相对较少，而针对无人飞行器飞行控制系统的设计，国内外相关专家已取得许多研究成果，主要包括智能PID、滑模控制、模糊控制、反步法等[2-6]。文献[3]利用反步滑模方法研究了网络环境下制导控制一体化算法的设计问题，但是没有考虑系统不确定性和外部干扰的影响;文献[4]通过模糊PID方法设计纵向控制器，但控制性能过度依赖模型的精度，难以达到实际效果;文献[5]利用模糊反步滑模设计了制导控制一体化系统，但是算法的数学过程繁琐，工程应用受到一定限制。

韩京清教授提出的自抗扰控制(ADRC)技术，继承了经典PID的诸多优点，又克服了它的很多缺点，具有卓越的控制效果和良好的扰动补偿能力，可以有效地应用于近程巡飞弹的姿态控制。

1 ADRC技术分析

1.1ADRC结构

与传统PID控制“基于误差来消除误差”的控制策略不同，ADRC对系统的“总和干扰”观测并加以补偿的一种综合控制方法，具有强大的扰动轨迹补偿能力[7-8]。

ADRC主要由跟踪-微分器 (TD)、非线性状态误差反馈组合控制律(NLSEF)和扩张状态观测器(ESO)3大部分构成,其结构如图1所示。

图1 ADRC结构图Fig.1 Structure of ADRC

1.2 ADRC算法

ADRC算法不依托于被控对象的模型，只针对输入u(k)和输出y(k)进行抗干扰控制。以二阶ADRC为例，具有扰动跟踪补偿能力的ADRC的完整算法如下[9]。

1) 以设定值v0为输入，TD安排输入参数的过渡过程，即

。

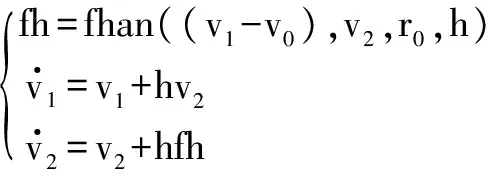
(1)

2) 以系统输出y和输入u来跟踪估计系统的状态和扰动，在ESO中完成

。

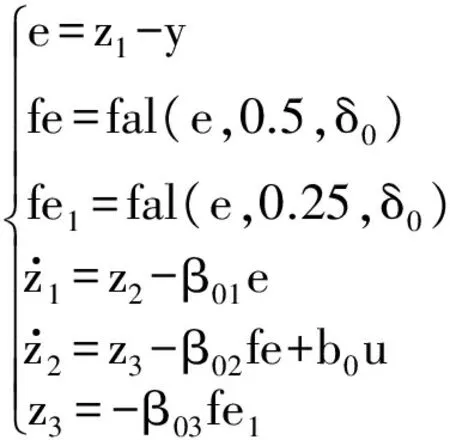
(2)

3) 非线性状态误差反馈，在NLSEF中完成

。

(3)

4) 扰动补偿。u0需要经过扩张状态估计值的补偿后，才能形成实际的控制量。控制量最终表达式为

。

(4)

fal()和fhan()的定义分别为

(5)

(6)

(7)

其中,h,r0,β01,β02,β03,α01,α02,δ0,η01,η02,α11,α12,δ1,b0都是ADRC的控制参数，其参数意义将在参数整定中详细介绍。

1.3ADRC方法改进设计与分析

在ESO中常用的非线性函数为式(5)中的fal()函数，但fal()函数并不是最优的非线性函数，虽然fal()在分段点处保证了连续性，但在分段点处小区间内不是光滑可导的，在某些状态下，如果参数δ值设定较小，fal()的导数将发生瞬变，从而引起输出发生大幅振荡，降低ADRC的控制性能[10]。针对该问题，对非线性函数进行研究，参考原fal()函数的性能，采用插值拟合的方法，提出在整个实数域光滑可导的fal1()，进而改进ADRC 的性能。

仅考虑|e|≤δ的情况，此时fal()为

。

(8)

对fal()进行三次多项式曲线拟合，由于fal()为奇函数，e2项的系数为零，且通常在δ取值较小的情况下,函数sine与指数函数e3具有相同的曲线形式，但前者的收敛特性较好，所以可设改进后的函数为

fal1(e,α,δ)=ae+csine

。

(9)

由函数需满足光滑性和连续性可得

(10)

求解可得

(11)

进而可得改进的函数形式为

(12)

对式(12)，取参数α=0.5，δ=0.1，则函数fal(e,α,δ)，fal1(e,α,δ)的曲线如图2所示。

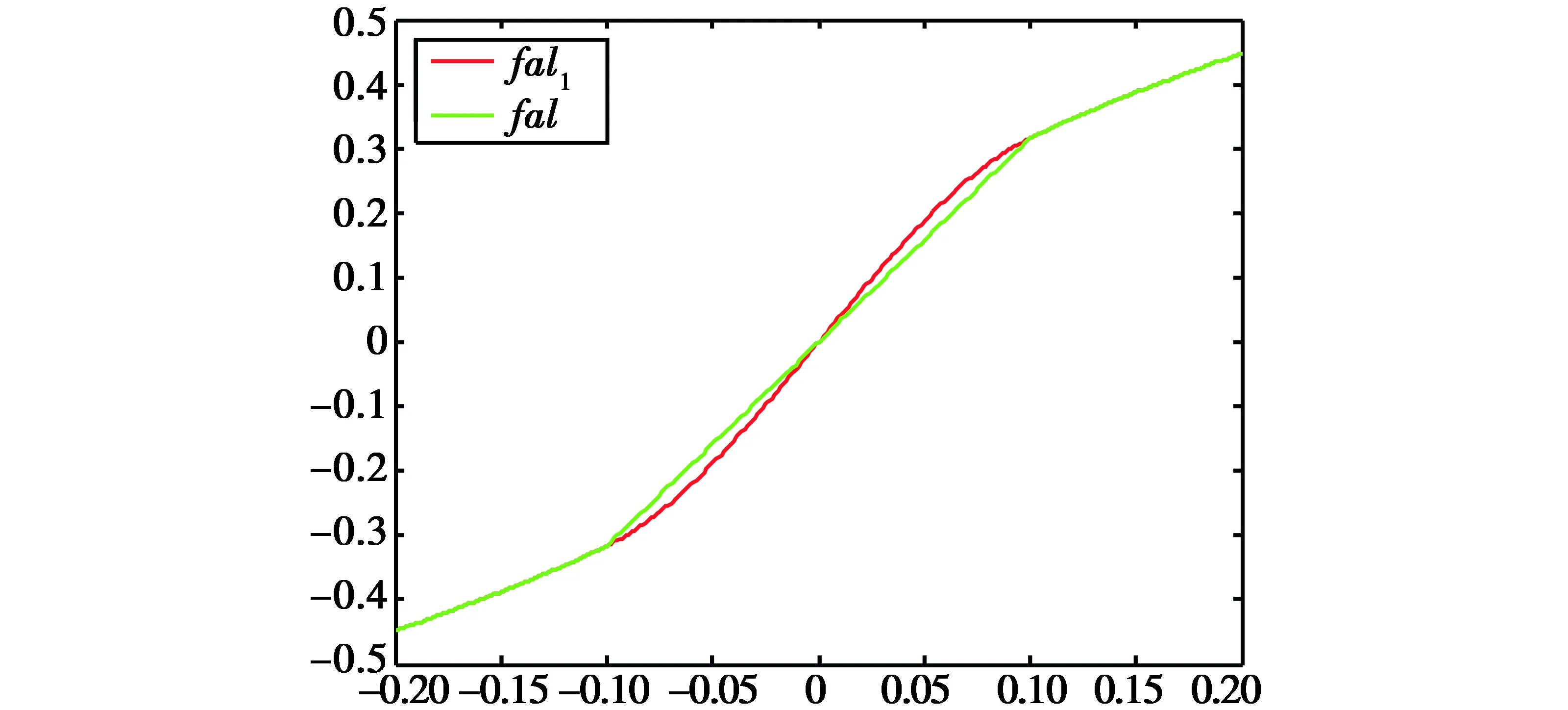
图2 fal1及fal的函数曲线Fig.2 fal1 and fal function curves

由图2可以看出，同样参数下,fal(e,α,δ)在分段函数连接位置存在明显不光滑现象，改进后的函数fal1(e,α,δ)连续光滑，验证了改进算法的合理性与正确性。

1.4 改进ADRC扰动估计补偿能力分析

为验证改进ADRC的扰动估计补偿性能，在Simulink平台下进行两种ADRC控制器受扰动条件下的阶跃响应分析。假设总和扰动为

。

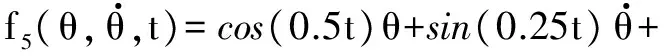
(13)

常规ADRC和改进的ADRC的参数经整定后为：r0=2,h=0.04,β01=100,β02=420,β03=2400,δ0=0.05,η01=55,η02=30，α11=0.75，α12=1.5，b0=10，δ=0.2，(δ0取值较小，为测验改进ADRC的性能)，Simulink仿真步长取0.01，系统阶跃响应以及ESO对系统“总和扰动”估计补偿的仿真曲线分别如图3和图4所示。

由图3可以看出，相比于常规ADRC在δ0较小时出现强烈的震颤现象，改进后的ADRC可以更好地跟踪控制俯仰角阶跃信号，系统跟踪阶跃信号无超调，无稳态误差，只有极小幅度的震颤，震颤误差峰值不超过千分之二。由图4可看出，相比于常规ADRC，改进后的ADRC可以更加准确、快速、实时地估计和补偿系统的“总体扰动”。验证了改进算法的合理性和有效性。

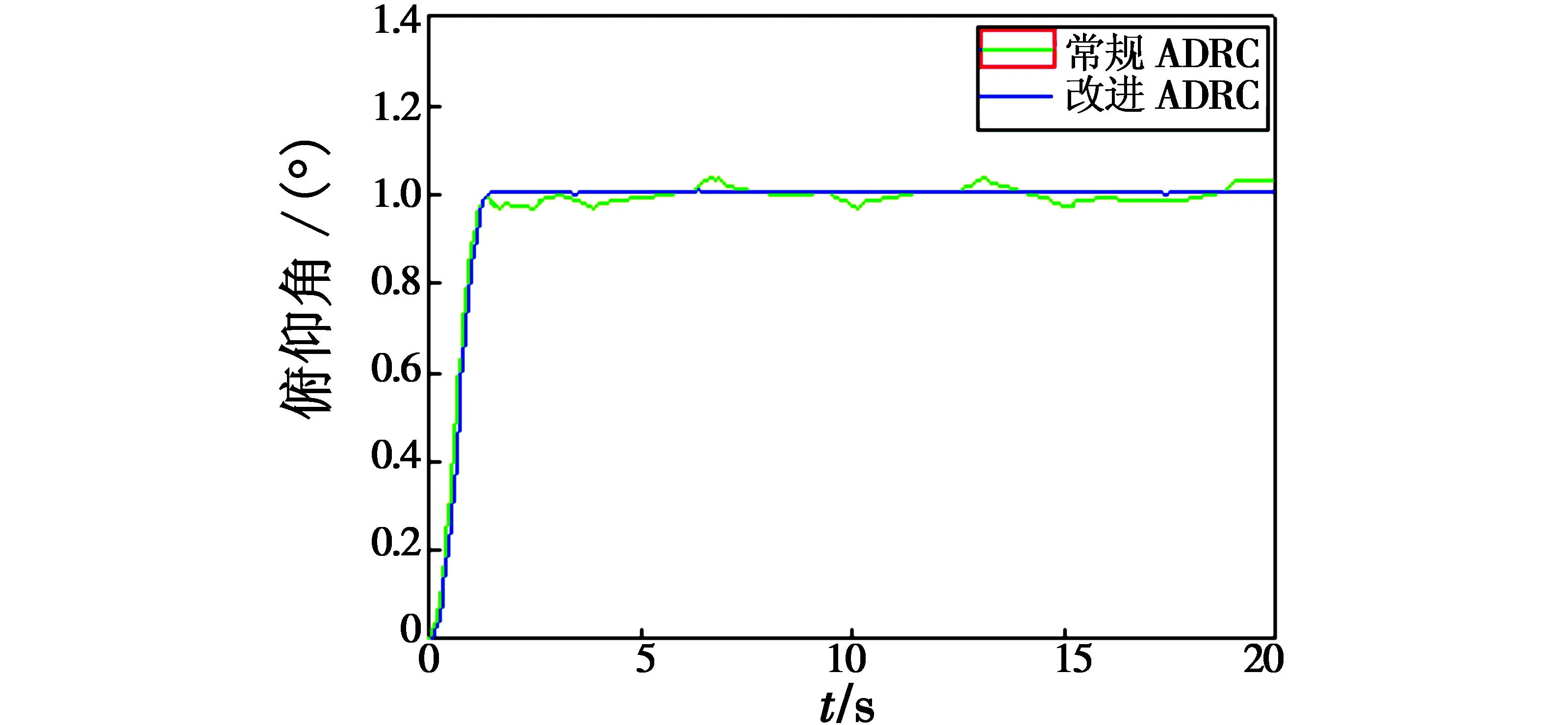
图3 两种ADRC下系统跟踪阶跃响应Fig.3 System step response based on two kinds of ADRC

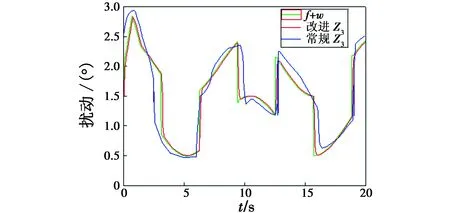
图4 两种ESO估计系统总和扰动Fig.4 Estimator of the total disturbances based on two kinds of ESO

2 基于改进ADRC的纵向巡飞控制系统设计

2.1 近程巡飞弹数学模型

近程巡飞弹飞行过程中的特性与无人机和巡航导弹相类似，且巡飞过程中过载较小、航线弧度小，俯仰通道的运动与其他两个通道之间的耦合较小，巡飞弹巡飞过程中的耦合一般指滚转通道与偏航通道之间的耦合，因此可将巡飞运动分解为横侧向运动和纵侧向运动，分别进行控制系统的设计，本文以纵向运动为例，进行巡飞控制系统的设计[11-12]。

近程巡飞弹纵向运动方程小扰动线性化处理后，得到状态空间方程式为

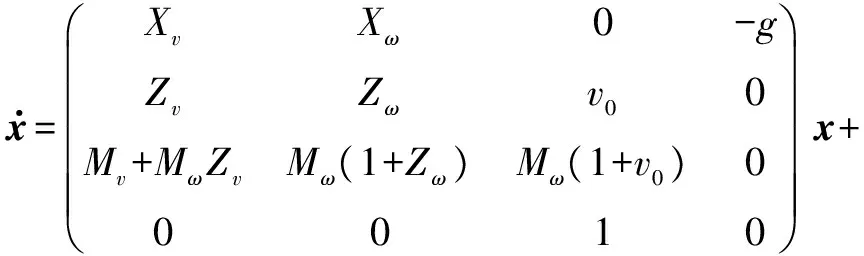
(14)

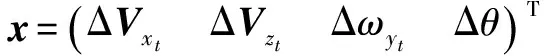
2.2 纵向运动ADRC设计

由于ADRC的ESO可以对系统的总体扰动进行估计并反馈补偿，假设电动机δT对水平巡飞速度的不确定性扰动为f1(x)，应用ESO反馈补偿，同理可得,其他状态量变化率的扰动分别为f2(x),f3(x),f4(x)，各控制量之间的耦合量算入系统“总和扰动”，这样即应用ADRC完成了各状态变量解耦[13-14]。得到简化后的运动方程为

。

(15)

根据上述对纵向运动的解耦分析，设计的纵向ADRC系统结构如图5所示。

图5 纵向运动ADRC原理图Fig.5 Schematic of longitudinal movement ADRC control

3 纵向运动控制数字仿真分析

为了验证改进的ADRC对纵向运动控制系统的控制效果，在Simulink平台下建立仿真模型，并进行仿真实验。为便于分析，选取无侧滑无滚转且无短时间爬升或下滑的运动状态作为近程巡飞弹的基准巡飞运动进行配平，所研究巡飞弹质量为15 kg,翼展0.8 m,气动弦长为0.3 m,机翼面积为0.24 m2,巡飞速度80 m/s,巡飞高度为400 m。

按照文献[15]的气动数据可进一步简化运动方程为

。

(16)

经过反复调整整定后，ADRC的参数如表1所示。

根据式(16)和图3的控制系统结构在Simulink环境下建立基于改进自抗扰的巡飞弹纵向运动控制系统和基于经典自抗扰的巡飞弹巡飞控制系统仿真模型，进行高度的跟踪与稳定实验(由于高度回路是纵向控制的最外层回路，也是最复杂的回路，高度指令的跟踪控制是在俯仰角和飞行速度的控制基础上实现的，所以仿真实验设计为高度的指令跟踪与稳定实验)。

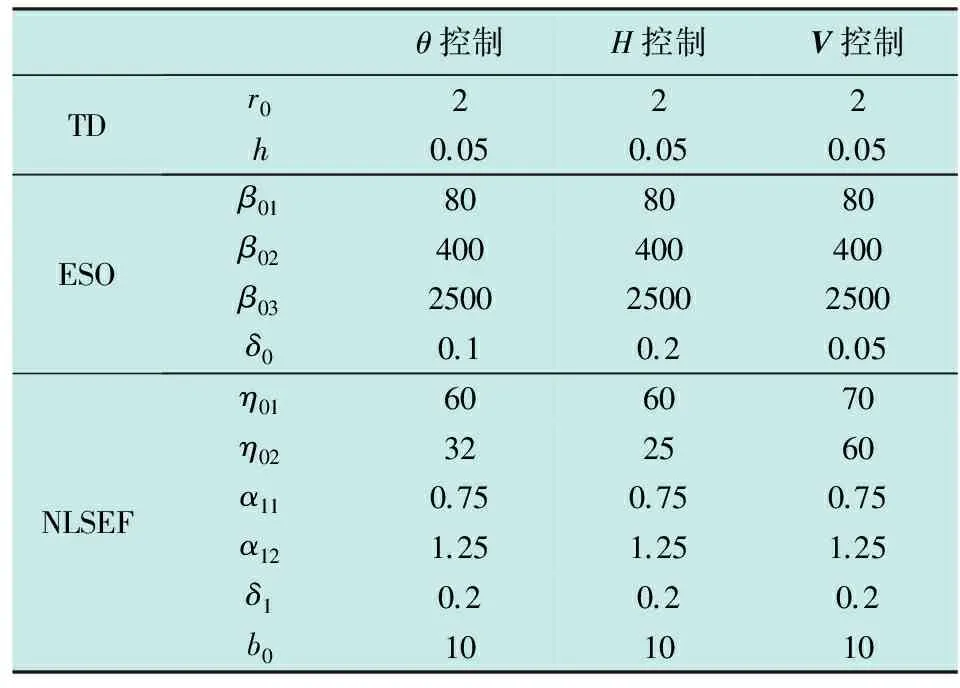
表1 ADRC仿真参数数值表

3.1 高度稳定仿真

在高度指令为幅值+15 m阶跃时间为2 s的输入调整高度时(此处,+15 m指高度偏差，实际高度应为H=H0+15 m，其中,H0为巡飞弹当前的巡飞高度)，采样周期T=0.01 s，进行仿真实验，系统的响应结果如图6所示。

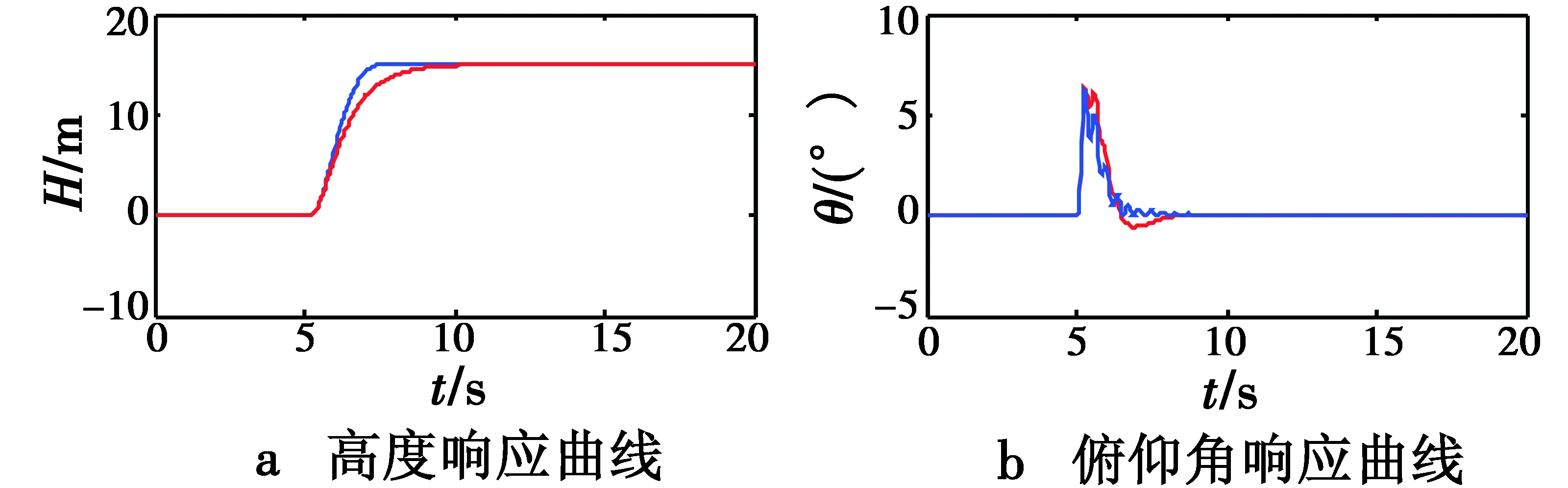
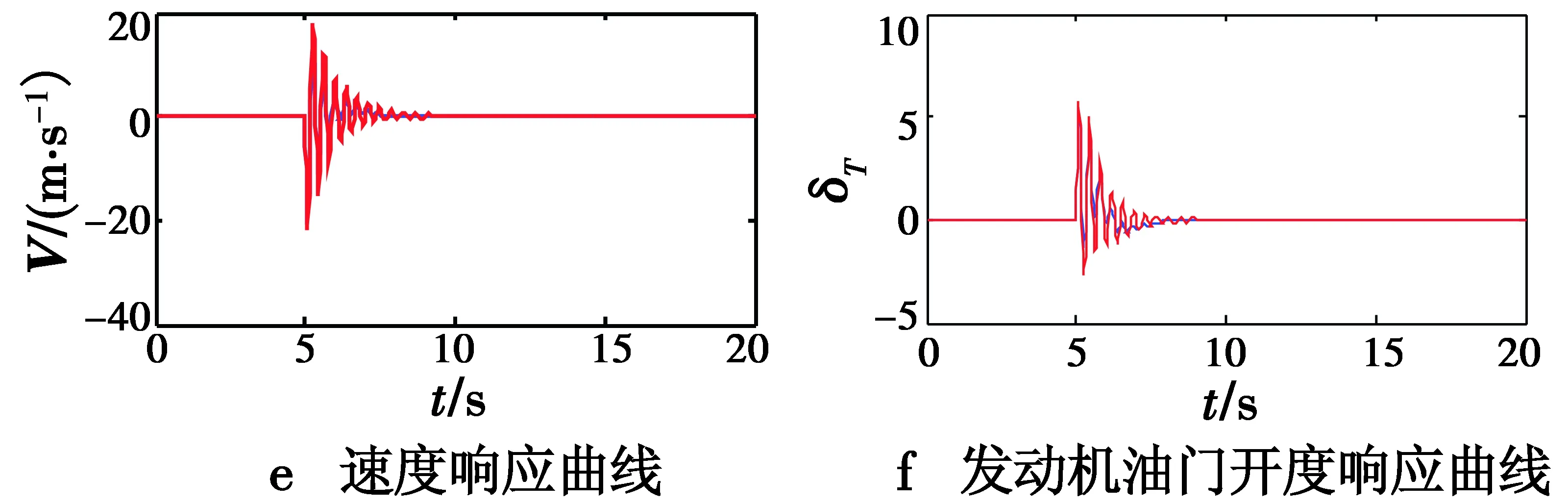
图6 系统响应结果Fig.6 System response result

图6中,红色、蓝色分别表示基于常规ADRC和改进后ADRC的纵向控制系统响应曲线。由图6可以看出，两个控制系统都能够完成高度的跟踪指令，然而改进后的ADRC系统调节时间为2.2 s，速度最大变化为12 m/s，原系统调节时间为4.5 s，速度最大变化量为18 m/s,舵机响应更加迅速准确、舵偏量小、调节能力强，可知改进后爬升过程中弹体抖动减小，高度稳定性更好。

3.2 抗干扰性能仿真

以高度控制为例，在仿真时间5 s处给高度添加幅值为1 m的脉冲干扰信号，调整自抗扰控制器的控制参数，高度响应如图7所示。由图7可见，改进后的ADRC系统降低了干扰产生的幅度变化，能更快消除干扰的影响，并增强对干扰的抑制能力。

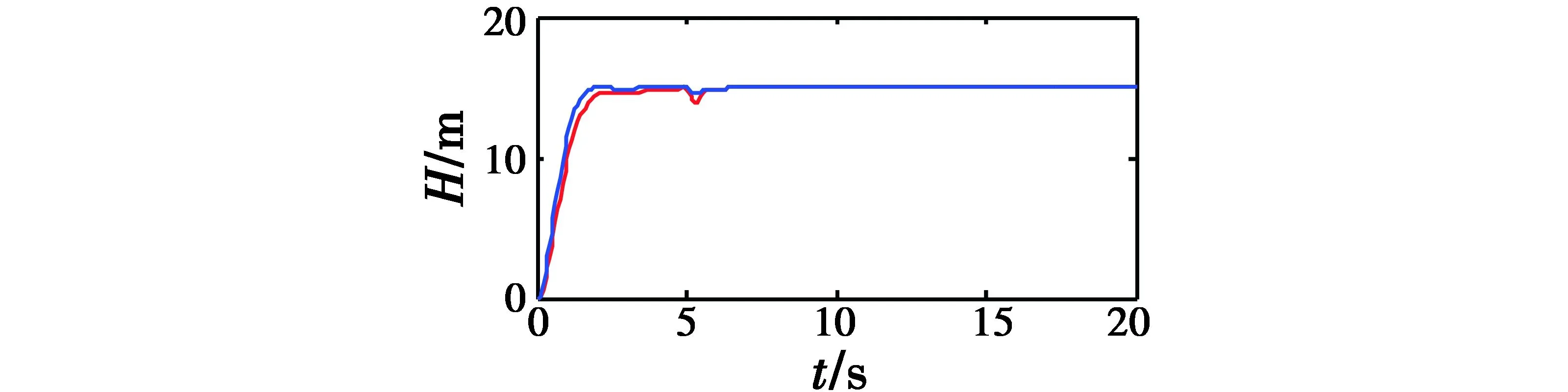
图7 抗干扰仿真曲线Fig.7 Anti-interference simulation curve

4 结束语

本文基于ADRC方法，提出了一种改进非线性函数的方法，使非线性函数整个实数范围内连续光滑可导，增大了ADRC参数调整范围，解决了震颤的问题，提高了ADRC的控制性能，并在改进的ADRC基础上，设计了近程巡飞弹纵向巡飞控制系统。通过仿真与常规ADRC控制系统的性能进行对比，结果验证了改进方法的正确可行性及所设计的横侧向自抗扰控制系统的有效合理性。

[1] 黄瑞,高敏,陈建辉.轻小型巡飞弹及其关键技术浅析[J].飞航导弹,2015(12):16-19.

[2] 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005.

[3] 杨君君,虞红志.一类离散时间系统的间接自适应模糊滑膜控制[J].电光与控制,2013,20(7):49-53.

[4] 王安,杨青青,闫文宇.模糊自整定PID控制器的设计与仿真[J].计算机仿真,2012(12):427-432.

[5] 王建敏,吴云洁,董小萌.基于滑模干扰观测器的高超声速飞行器滑模控制[J].航空学报,2015,36(6):2027-2036.

[6] 刘杰,赵辉,翁兴伟.基于改进Fuzzy-PID控制理论的无人机纵向飞控律设计[J].电光与控制,2012,19(1):57-61.

[7] LIU F C,CHEN X,JIA Y F.Application of fuzzy ADRC in flexible spacecraft vibration suppression[J].Journal of Vibration and Shock,2015,34(9):9-14.

[8] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.

[9] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.

[10] 邱搏博.高超声速飞行器改进自抗扰控制方法研究[D].哈尔滨：哈尔滨工业大学,2014.

[11] 涂海峰.巡飞弹药系统建模与导航控制技术研究[D].北京:北京理工大学,2015.

[12] 黄健.自抗扰技术在水下航行体横滚姿态控制中的应用研究[J].船舶工程,2014,36(1):131-135.

[13] 宋金来,金岳.制导炸弹滚转通道自抗扰控制设计方法研究[J].航天控制,2014,32(6):26-30.

[14] 石晨曦.自抗扰控制及控制器参数整定方法的研究[D].无锡：江南大学,2008.

[15] 肖培春.基于模糊控制的巡飞弹飞行控制系统设计与仿真研究[D].南京：南京理工大学,2012.

OnVerticalControlSystemofLoiteringMissileBasedonImprovedADRC

HUANG Rui, CHEN Jian-hui, GAO Min, TAO Gui-ming

(Ordnance Engineering College,Shijiazhuang 050003,China)

Considering the problems of nonlinearity,uncertainty,and coupling existed in system model of longitudinal control system of short-range loitering missile,Active Disturbance Rejection Controller (ADRC) is integrated to deal with them.The structure,principle,algorithm implementation and parameter setting rules of ADRC are presented here.As to the trembling phenomenon and control performance degradation when the linear interval width of Extended State Observer (ESO)is small,a method of improved nonlinear function is proposed for design of the longitudinal motion control system.The result of simulation experiments with Simulink platform show that:1) The improved method effectively solves the problem of trembling and enhances the controller performance;and 2) The control system based on improved ADRC has good control performance.Therefore,the rationality of the improved method and control system is verified.

ADRC; attitude control; loitering missile; Simulink; anti-jamming capability

黄瑞,陈建辉,高敏,等.基于改进ADRC的巡飞弹纵向控制系统研究[J].电光与控制，2017，24(7)：41-45.HUANG R,CHEN J H,GAO M,et al.On vertical control system of loitering missile based on improved ADRC[J].Electronics Optics & Control,2017,24(7):41-45.

V249.122+.2

A

10.3969/j.issn.1671-637X.2017.07.009

2016-06-27

2016-09-07

装备预研基金项目(9140A25070509JB3405)

黄 瑞(1991 —),男，湖北襄阳人，硕士生，研究方向为精密仪器与微系统。重要组成部分。巡飞控制的性能直接关系到侦察、搜索、打击等作战任务的执行情况，是近程巡飞弹研发设计的关键技术之一。