分块稀疏信号1-bit压缩感知重建方法∗
丰卉孙彪 马书根2)
1)(天津大学电气自动化与信息工程学院,天津 300072)
2)(立命馆大学机器人系,滋贺 5258577)
分块稀疏信号1-bit压缩感知重建方法∗
丰卉1)孙彪1)†马书根1)2)
1)(天津大学电气自动化与信息工程学院,天津 300072)
2)(立命馆大学机器人系,滋贺 5258577)
1-bit压缩感知,变分贝叶斯推断,分块稀疏
1 引 言
近年来,由于压缩感知理论[1,2]能够在远低于内奎斯特采样数量的条件下对信号进行精确重建,引起了研究人员的广泛关注.目前,压缩感知已经在频谱感知[3]、超分辨成像[4−6]、图像处理[7]、神经信号采集[8−11]等领域获得了广泛应用.压缩感知过程可以表示为

其中x∈RN×1表示原始信号,y∈RM×1表示压缩采样值,M≪N,Φ∈RM×N表示测量矩阵,n∈RM×1表示测量噪声.
传统压缩感知假设压缩采样值具有无限高的精度,但是在实际应用场景中,压缩采样值必须经过量化才能进行传输和保存.常用的量化级有8 bit,12 bit等.随着量化级的提高,压缩感知的硬件实现难度也会相应增加.1-bit压缩感知[12,13]是压缩感知中的特例,只保留压缩采样值的符号信息,显著减少了压缩采样数据量.1-bit压缩感知过程表示如下:

1-bit压缩感知的目的是利用最小数量的bit数对信号进行重建,在1-bit压缩感知中,bit总数等于量化深度与1-bit压缩采样数量的乘积,由于量化深度为1,即使当采样数量M的值比较大时,bit总数也会相对较低,因此存在M>N.至今为止,研究人员已经提出了一系列1-bit压缩感知重建算法,典型算法有符号匹配追踪(matching sign pursuit)算法[14],二进制迭代硬阀值(binary iterative hard thresholding,BIHT)算法[15],量化变分消息传递(quantized variational message passing,QVMP)[16]等.值得注意的是,这些算法都是针对稀疏信号的重建算法,当信号难以进行稀疏表达时,这些算法则无法对信号进行精确重建.常见的化学气体浓度信号[17,18],脑电图信号[19]、光电容积脉搏波(photoplethysmography,PPG)信号[20]等信号无法使用常见的稀疏基(如离散余弦变换基、离散小波变换基等)进行稀疏表达,从而限制了1-bit压缩感知方法的应用.
本文提出了一种基于分块稀疏信号模型的1-bit压缩感知重建方法.该方法利用分块稀疏的统计特性对信号进行数学建模,利用变分期望最大化(variational expectation maximization,VEM)算法进行信号重建.在PPG信号上的重建实验表明,该算法能够在较低采样数据量前提下精确重建原始信号.
本文中黑体大写斜体字母(例如A)表示矩阵,黑体小写斜体字母(例如x)表示向量,非黑体字母(例如c)表示标量.对于向量x,xi表示向量x的第i个元素,表示ℓ2范数. 对于方阵A1,···,Ag,diag{A1,···,Ag}表示块对角线为A1,···,Ag的块对角矩阵.对于随机变量a,p(a)表示其概率密度函数.N(µ,Σ)表示均值为µ,方差为Σ的高斯分布.
2 基于分块稀疏信号模型的1-bit压缩感知重建算法
2.1 分块稀疏模型
信号的分块模型可以表示为


其中γi是非零参数,表示控制信号x的分块稀疏性的参数,当γi=0时,对应的分块内的元素为零;Bi∈Rdi×di是正定矩阵,表示分块内部的相关性结构.假设块与块之间不相关,x的先验分布可以表示为


假设测量噪声n服从高斯分布:

其中λ是大于零的标量.
根据文献[22],1-bit压缩采样值z的似然函数可以表示为

其中σ(y)∆=1/(1+exp(−y))是logistic函数.
2.2 变分贝叶斯推断
在贝叶斯压缩感知框架中,通过贝叶斯推断以及最大后验估计进行信号重建,但是在1-bit压缩感知中通过贝叶斯推断难以得到准确的后验估计,因此,本文采用变分贝叶斯推断方法[23]进行信号重建.1-bit压缩采样值z的边缘概率密度函数表示为

其中

本文中,x,n是需要估计的变量,x是表征原始信号的随机变量,n是表征测量噪声的随机变量,二者相互独立;θ∆={x,n},其中q(θ)表示概率密度函数;KL(q∥p)表示KL散度(Kullback-Leibler divergence),最大化L(q)等价于最小化KL(q∥p),因此通过最大化L(q)近似估计后验概率p(θ|z)得到q(θ).
我们的目的是通过最大化L(q)寻找p(x|z),p(n|z)的近似估计q(x)以及q(n).其中

根据(8)式可知,由于p(z|x,n)中存在logistic函数,L(q)中的积分部分难以计算,因此通过最大化L(q)的下界近似得到q(x)以及q(n).通过Jaakkola-Jordan不等式[24]得到




根据文献[23],在变分推断中,q(θ)是变量x,n的联合分布函数,x是具有分块稀疏先验的随机变量,n是具有高斯先验的随机变量,变量x,n相互独立,因此有分解形式q(θ)=q(x,n)=q(x)q(n),并且有

进一步通过VEM算法,对未知变量和超参数进行推断.在E步中,近似估计后验分布;在M步中,由于是L(q)的下界,因此通过最大化下界逐步逼近L(q)的最大值.具体步骤如下.
E步:首先更新q(x),根据(15)和(17)式,q(x)可以近似估计为


其中µn表示后验分布q(n)的均值.
其次,更新q(n),q(n)可以近似估计为

通过(24)式可知q(n)服从高斯分布,均值µn和方差矩阵Σn可以表示为

M步:通过将q(θ;Θold)代入˜L(q,Θ),Θ可以通过以下方式进行估计:
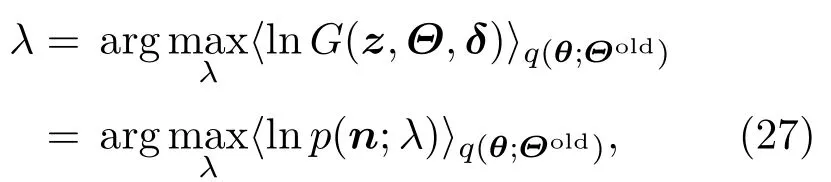
因此,

通过对变量λ求导得到

使导数为零,可以得到


因此


通过对变量γi以及Bi求导得到

使导数为零,可以得到

为了进一步提升算法性能,根据文献[21],对Bi进行正则化.将分块xi内元素建模为一阶自回归过程,并且具有平滑先验,即

其中xi,k表示分块xi中的第k个元素,1 6k6di,r是自相关系数,r∈(−1,1),并且表征信号的平滑程度,r=m1/m0,m1是Bi的主对角线平均值,m0是Bi的副对角线平均值.假设p(ωi,k)=N(0,γi),进一步可以得到p(xi,k)=N(0,γi),在该假设下,对应的分块元素的协方差ˆBi为对称Toeplitz矩阵,即

因此,用Toeplitz矩阵ˆBi正则化Bi不仅使其需要估计的参数变少,并且Toeplitz矩阵对一阶自回归模型建模时,可以表征信号的平滑程度,当信号具备平滑先验时,其重建性能就会得到提高.且

因此,

通过对变量δi求导得到

使导数为零,可以得到

本文算法如表1所列.

表1 本文算法步骤Table 1.The proposed algorithm procedures.
本文的算法在(2)式所示的1-bit压缩感知模型上进行重建.算法不但可以在时域中进行重建,也可以在变换域中进行重建.当信号在时域中重建时,算法通过z,Φ得到时域重建信号ˆx;当信号在变换域Ψ中进行重建时,x=Ψs,令Ω=ΦΨ,算法通过z,Ω得到变换域中的重建信号ˆs,通过变换ˆx=Ψˆs得到时域信号.根据以上描述可知,本文算法既可以在时域重建信号,也可在变换域重建信号.为了评估算法在时域和变换域重建的性能,在实验结果及分析中,分别进行了时域和变换域重建实验.
3 实验结果与分析
为了验证算法的有效性,采用PPG信号片段作为待压缩信号.PPG信号可以用于开发便携、可穿戴心率传感设备.在实际情况中,人体运动状态的改变会引入运动伪迹,尤其是剧烈运动时运动伪迹会严重干扰PPG信号,难以进行合适的稀疏表达.本文采用手腕处采集得到的PPG信号[25,26],采样频率为31.75 Hz,选取PPG信号长度N=128.
本文选择以下算法作为对比算法.

图1 (网刊彩色)不同算法的重建效果,M=256 (a)PPG信号片段;(b)PPG信号1-bit压缩采样值分布;(c)BIHT重建效果;(d)QVMP重建效果;(e)R1-BCS重建效果;(f)本文算法(时域)重建效果;(g)本文算法(DCT域)重建效果Fig.1.(color online)Reconstruction of different algorithms:(a)PPG signal fragment;(b)distribution of 1-bit compressed samplings;(c)reconstruction of BIHT;(d)reconstruction of QVMP;(e)reconstruction of R1-BCS;(f)reconstruction of the proposed algorithm(time domain);(g)reconstruction of the proposed algorithm(DCT domain).
1)QVMP[16].QVMP是一种变分贝叶斯反量化算法,QVMP不能直接在时域中对信号进行重建,因此本文将QVMP在变换域中进行信号重建:

其中,Ψ是已知的稀疏变换矩阵,s是稀疏系数,QVMP算法首先得到,随后得到重建信号
2)BIHT[15]. BIHT是一种迭代算法,同QVMP,只能在变换域中进行信号重建.
3)R1-BCS[27].R1-BCS是一种基于高斯-伽马先验的变分贝叶斯算法,同上,只能在变换域中进行信号重建.
实验中,以上算法均选取离散余弦变换(discrete cosine transform,DCT)矩阵作为稀疏变换矩阵.采用重建信噪比(reconstruction signal noise ratio,RSNR)作为信号重建精度的考察指标,RSNR定义为

本文选择的测量矩阵为高斯随机矩阵,并且对测量矩阵的每一列进行归一化.
图1是本文中提出的1-bit压缩感知重建方法和其他1-bit压缩感知重建方法的效果图,1-bit压缩采样值的数量M=2N.如图1所示,其中图1(a)是PPG片段的示意图;图1(b)是1-bit压缩采样值z=sign(Φx+n)的分布;图1(c)表示BIHT算法的信号重建效果,从RSNR以及重建信号可以看出,BIHT算法应用在PPG信号实验中,性能相对较差;图1(d)和图1(e)分别表示QVMP算法和R1-BCS算法的重建效果,其重建效果明显优于BIHT;图1(f)和图1(g)表示本文算法的重建效果,图1(f)是在时域中的重建效果,图1(g)是在余弦变换域中的重建效果.实验结果表明,本文提出的算法重建效果明显优于其他算法.图2显示了不同数量的1-bit压缩采样值对算法重建性能的影响,可以看出,1-bit压缩采样值数量越多,算法的重建性能越好.在图2中,M=0.5N,N,···,3.5N,4N,随着M的增加,所有的算法的性能明显得到提高.本文算法在DCT域中和其他算法相比,重建效果明显优于其他算法.由于本文算法能够在时域中对信号进行重建,因此,将时域的重建效果与其他算法在DCT域中的重建效果进行比较,实验结果证明,在时域中重建信号,本文的算法依旧优于其他算法在DCT域中的重建效果.传统压缩感知需要寻找合适的稀疏表达,当信号难以找到合适的稀疏表达,传统压缩感知方法重建效果不佳,本文的分块稀疏模型利用元素间的相关性对信号进行建模,通过变分贝叶斯推断方法获得模型参数,重建原始信号,从而避免了稀疏表达的过程,因而对非稀疏信号有更好的重建性能.本文提出的算法在时域中重建,和重建效果较好的R1-BCS算法相比,RSNR提高了1.5 dB,在DCT域中重建,RSNR和R1-BCS算法相比提高了3.9 dB.由于在DCT域中重建信号,正则化后的ˆBi更精确地表达分块内部的相关性,因此在DCT域中重建效果较其在时域中的重建效果更好.实验结果证明,本文算法无论在时域还是稀疏域,都可以对信号进行重建,并且当信号难以确定合适的稀疏表达时,本文的算法可以获得比其他算法更加精确的结果.

图2 (网刊彩色)不同数量的1-bit压缩采样值对应的RSNR趋势变化Fig.2.(color online)The RSNR trend of different 1-bit compressed samplings.
图3是不同压缩采样值数量对应的算法执行时间.从图3来看,本文的算法在执行时间和其他算法相比有所不足.这是由于本文算法在执行过程中存在多步矩阵求逆运算,影响了算法的执行效率.随着1-bit压缩采样值数量的增加,算法在执行过程中涉及到的矩阵的维数相应增加,使得矩阵求逆运算需要更多的时间.图4是当M=2N时,不同算法的收敛速度.如图4(a)所示,随着迭代次数的增加,本文的算法在迭代次数为40时,算法已经达到收敛,而其他算法明显还需要更多的迭代次数,尤其是BIHT和QVMP算法,如图4(b)所示,这两种算法达到收敛所需要的迭代次数远高于其他算法.

图3 (网刊彩色)不同数量的1-bit压缩采样值对应算法执行时间变化Fig.3.(color online)The execution time of different 1-bit compressed samplings.

图4 (网刊彩色)(a)M=256,不同算法的收敛速度;(b)M=256,BIHT,QVMP算法的收敛速度Fig.4.(color online)(a)M=256,the convergence rate of different algorithms;(b)M=256,the convergence rate of BIHT and QVMP.
4 讨 论
传统的1-bit压缩感知信号重建方法主要目标集中在重建稀疏信号,当信号难以找到合适的稀疏表达时,传统的1-bit压缩感知信号重建方法效果不佳,而在实际应用中,存在很多信号难以找到合适的稀疏表达,传统的1-bit压缩感知方法无法得到应用,本文的算法基于分块稀疏模型,利用分块内部元素之间的相关性,对分块稀疏模型进行高斯建模,对分块稀疏模型的概率建模避免了寻找稀疏表达过程.通过变分贝叶斯推断得到重建信号的近似后验概率分布,并且用VEM算法对超参数进行了估计.通过实验验证,算法存在一定的优势.
5 结 论
本文提出了一种针对分块稀疏信号的1-bit压缩感知重建算法,该算法利用分块稀疏的统计特性对信号进行数学建模,之后采用变分贝叶斯方法进行信号重建.该算法和其他传统1-bit压缩感知重建算法相比,重建性能具有明显的优越性.
[1]Donoho D L 2006IEEE Trans.Inf.Theory52 1289
[2]Candes E J,Romberg J,Tao T 2006IEEE Trans.Inf.Theory52 489
[3]Zhang J C,Fu N,Qiao L Y,Peng X Y 2014Acta Phys.Sin.63 030701(in Chinese)[张京超,付宁,乔立岩,彭喜元2014物理学报63 030701]
[4]Li L Z,Yao X R,Liu X F,Yu W K,Zhai G J 2014Acta Phys.Sin.63 224201(in Chinese)[李龙珍,姚旭日,刘雪峰,俞文凯,翟光杰2014物理学报63 224201]
[5]Li S D,Chen W F,Yang J,Ma X Y 2016Acta Phys.Sin.65 038401(in Chinese)[李少东,陈文峰,杨军,马晓岩2016物理学报65 038401]
[6]Li S D,Chen Y B,Liu R H,Ma X Y 2017Acta Phys.Sin.66 038401(in Chinese)[李少东,陈永彬,刘润华,马晓岩2017物理学报66 038401]
[7]Ning F L,He B J,Wei J 2013Acta Phys.Sin.62 174212(in Chinese)[宁方立,何碧静,韦娟 2013物理学报 62 174212]
[8]Sun B,Zhao W F,Zhu X S 2017J.Neural Eng.14 036018
[9]Sun B,Feng H,Chen K F,Zhu X S 2016IEEE Access4 5169
[10]Sun B,Feng H 2017IEEE Signal Process.Lett.24 863
[11]Sun B,Ni Y M 2017IEEE Commun.Lett.21 1775
[12]Boufounos P T,Baraniuk R G 2008Proceedings of the 42nd Annual Conference Information Sciences and SystemsPrinceton,USA,March 19–21,2008 p16
[13]Sun B,Jiang J J 2011Acta Phys.Sin.60 110701(in Chinese)[孙彪,江建军 2011物理学报 60 110701]
[14]Boufounos P T 2009Proceedings of the 43rd Asilomar Conference Signals,Systems and ComputersPaci fic Grove,USA,November 1–4,2009 p1305
[15]Jacques L,Laska J N,Boufounos P T,Baraniuk R G 2013IEEE Trans.Inf.Theory59 2082
[16]Yang Z,Xie L,Zhang C 2013IEEE Trans.Signal Process.61 2815
[17]Meng Q H,Li F 2006Robot28 89(in Chinese)[孟庆浩,李飞2006机器人28 89]
[18]Cao M L,Meng Q H,Zeng M,Sun B,Li W,Ding C J 2014Sensors14 11444
[19]Zhang Z,Jung T P,Makeig S,Rao B 2013IEEE Trans.Biomed.Eng.60 221
[20]Zhang Z L 2014Proceedings of IEEE Global Conference on Signal and Information ProcessingAtlanta,USA,December 3–5,2014 p698
[21]Zhang Z L,Rao B 2013IEEE Trans.Signal Process.61 2009
[22]Tipping M 2001J.Mach.Learn.Res.1 211
[23]Tzikas D G,Likas A C,Galatsanos N P 2008IEEE Signal Process.Mag.25 131
[24]Bishop C M,Tipping M E 2000Proceedings of the 16th Conference Uncertainty in Artificial IntelligenceSan Francisco,USA,June 30–July 3,2000 p46
[25]Sun B,Feng H,Zhang Z L 2016Proceedings of the 41st IEEE International Conference on Acoustics,Speech,and Signal ProcessingShanghai,China,March 20–25,2016 p809
[26]Sun B,Zhang Z L 2015IEEE Sens.J.15 7161
[27]Li F,Fang J,Li H,Huang L 2015IEEE Signal Process.Lett.22 857
One-bit compressed sensing reconstruction for block sparse signals∗
Feng Hui1)Sun Biao1)†Ma Shu-Gen1)2)
1)(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
2)(Department of Robotics,Ritsumeikan University,Shiga-ken 5258577,Japan)
14 March 2017;revised manuscript
15 May 2017)
Data compression is crucial for resource-constrained signal acquisition and wireless transmission applications with limited data bandwidth.In such applications,wireless data transmission dominates the energy consumption,and the limited telemetry bandwidth could be overwhelmed by the large amount of data generated from multiple sensors.Conventional data compression techniques are computationally intensive,consume large silicon area and o ff set the energy bene fits from reduced data transmission.Recently,compressed sensing(CS)has shown potential in achieving compression performance comparable to previous methods but it has simpler hardware.Especially,one-bit CS theory proves that the signs of compressed measurements contain sufficient information about signal reconstruction,gives that the signals are sparse or compressible in specific dictionaries,thus demonstrating its potential in energy-constrained signal recording and wireless transmission applications.However,the sparsity assumption is too restrictive in many actual scenarios,especially when it is difficult to seek sparse representation for signals.In this paper,a novel one-bit CS method is proposed to reconstruct the signals that are difficult to represent with traditional sparse models.It is capable of recovering signal with comparable compression ratio but avoiding the dictionary selection procedure.
The proposed method consists of two parts.1)The block sparse model is adopted to enforce the structured sparsity of the signals.It not only overcomes the drawbacks of conventional sparse models but also enhances the signal representation accuracy.2)The probabilistic model of one-bit CS procedure is constructed.Because of the existence of logistic function in probabilistic model of one-bit CS,the Bayesian inference cannot be used to proceed,and the variational Bayesian inference algorithm is developed to reconstruct the original signals from one-bit measurements.
Various experiments on different quantities of compressed measurements and iterations are carried out to evaluate the recovery performance of the proposed approach.The photoplethysmography(PPG)signals recorded from subject wrist(dorsal locations)by using PPG sensors built in a wristband are selected as the validation data because they are difficult to represent with traditional sparse dictionaries.The experimental results reveal that the proposed approach outperforms the state-of-the-art one-bit CS method in terms of both reconstruction accuracy and convergence rate.
Compared with prior method on one-bit CS,the proposed method shows competitive or superior performance in three aspects.Firstly,by adopting the block sparse model,the proposed method improves the capability to compress signals that are difficult to represent with traditional sparse models,thus making it more practical for long term and real applications.Secondly,by embedding the statistical properties of the one-bit measurements into the recovery algorithm,the proposed method outperforms other one-bit CS methods in terms of both reconstruction performance and convergence speed.Finally,energy and computational efficiency of the proposed method make it an ideal candidate for resource-constrained,large scale,multiple channel signal acquisition and transmission applications.
one-bit compressed sensing,variational Bayesian inference,block sparse
PACS:02.30.Zz,02.50.–r,87.16.dt,84.40.UaDOI:10.7498/aps.66.180202
*Project supported by the National Natural Science Foundation of China(Grant Nos.61401303,51578189).
†Corresponding author.E-mail:sunbiao@tju.edu.cn
(2017年3月14日收到;2017年5月15日收到修改稿)
1-bit压缩感知理论指出:对稀疏信号进行少量线性投影并对投影信号进行1-bit量化,该1-bit信号包含足够的信息,从而能对原始信号进行高精度重建.然而,当信号难以进行稀疏表达时,传统1-bit压缩感知算法无法精确重建原始信号.前期研究表明,分块稀疏模型作为一种特殊的结构型稀疏模型,对于难以用传统稀疏模型进行表达的信号具有较好的表达作用.本文提出了一种针对分块稀疏信号的1-bit压缩感知重建方法,该方法利用分块稀疏的统计特性对信号进行数学建模,通过变分贝叶斯推断方法进行信号重建并在光电容积脉搏波(photoplethysmography)信号上进行了实验验证.实验结果表明,与现有1-bit压缩感知重建方法相比,本文方法重建精度更高,且收敛速度更快.
10.7498/aps.66.180202
∗国家自然科学基金(批准号:61401303,51578189)资助的课题.
†通信作者.E-mail:sunbiao@tju.edu.cn

