时域混合算法在一维海面与舰船目标复合电磁散射中的应用∗

王强 郭立新

1)(西安电子科技大学物理与光电工程学院,西安 710071)

2)(陕西学前师范学院计算机与电子信息系,西安 710100)

时域混合算法在一维海面与舰船目标复合电磁散射中的应用∗

王强1)2)郭立新1)†

1)(西安电子科技大学物理与光电工程学院,西安 710071)

2)(陕西学前师范学院计算机与电子信息系,西安 710100)

粗糙海面,混合方法,时域积分方程,瞬态电磁散射

1 引 言

粗糙面与目标复合电磁散射研究是电磁波散射领域较为复杂且具有实际应用价值的研究课题.例如:风驱起伏海面上的舰船、掠空飞行的海上目标、陆地上的战车以及地表植被等粗糙面环境下雷达目标的探测等都是这种模型.

随机粗糙面与目标复合电磁散射的求解主要包括近似的解析方法、数值方法、解析-数值混合方法.近似的解析方法有基尔霍夫近似(KA)[1]、小斜率近似[2]以及相位微扰法[3]等.这些近似的解析方法具有较高的计算效率,但受一定条件的限制.例如:KA方法适用于小入射角且粗糙面起伏比较平缓的情形.数值方法包括矩量法(MoM)[4]、有限元方法(FEM)[5]、时域有限差分(FDTD)方法[6]、时域积分方程(TDIE)方法[7]等,这些数值方法计算精确,但在计算电大尺寸粗糙面时存储量过大且计算效率低下.为了保持传统数值算法的准确性,同时加快求解速度,近年来不断有研究工作报道解析方法结合数值方法的混合算法.Wang等[8]提出了基于电流计算的MoM-KA混合算法,分析了一维粗糙海面与上方导体目标的双站复合电磁散射特性.He和Zhu[9]用MoM-KA混合法结合UV技术分析了一维粗糙面与二维目标的复合电磁散射.Li等[10]用有限元-边界积分方法与基尔霍夫近似方法的混合算法求解了二维介质目标与粗糙海面的复合电磁散射.在这些混合算法中,对粗糙面上方的目标采用精确的数值方法(如:MoM,FEM)求解,而大尺度的粗糙面则采用近似的解析方法KA求解[8−11].

随着脉冲技术在微波与毫米波通信、雷达、遥感等领域的广泛应用,与脉冲有关的时域电磁场研究引起了很多学者的广泛关注.在瞬态宽带电磁散射计算中,频域算法计算效率远不如时域算法.频域算法需要对每个频率点采样,计算效率较低,时域算法只需一次计算就可得到宽频带响应[7].Wang等[7]利用TDIE方法研究了一维随机粗糙面与上方二维导体目标复合瞬态电磁散射特征.Li等[12]利用FDTD方法计算了一维粗糙面与上方二维导体目标的宽带电磁散射特性.Yang等[13]提出了FDTD方法与时域物理光学(TDPO)方法的混合算法计算三维组合目标的瞬态远场响应.实际上,TDPO方法在单独用于粗糙面电磁散射计算时就称为时域基尔霍夫近似(TDKA)方法.值得一提的是,目标与粗糙面复合电磁散射的FDTD-TDKA混合算法至今未见报道.秦三团等[11]提出用TDIE方法与TDKA方法的混合算法来求解一维随机粗糙面与上方二维导体目标的复合瞬态电磁散射.在TDKA方法中,粗糙面上的表面场用切向场做近似处理.因此,粗糙面上每一点都要求具有较大的曲率半径[11].TDIE-TDPO混合算法在组合目标电磁散射中的应用已有一些报道[14−17].然而,对于目标与粗糙面复合瞬态电磁散射的TDIE-TDKA混合算法研究,目前国内外报道极少.在实际大尺度复杂海面与地面散射问题中,往往需要对大尺度复杂海面与地面进行模拟,计算过程中未知量数目巨大.因此,如何快速求解未知量是当前时域电磁学的一个重要研究方向.目前,粗糙面与目标复合散射的混合方法大多是基于频域的混合算法,并且仅仅应用于粗糙面与上方目标复合电磁散射计算.采用TDIE方法以及基于TDIE方法的混合算法对于粗糙面复合散射问题的研究工作鲜有报道.TDIE-TDKA混合算法在粗糙面与目标复合瞬态电磁散射特性快速算法建模及其应用领域仍需做进一步探索.

本文首次将TDIE-TDKA混合算法延伸到粗糙海面与舰船目标复合电磁散射研究中,进一步拓展了解析-数值混合算法的应用范围.通过TDIETDKA混合算法与传统TDIE算法结果的对比,表明TDIE-TDKA混合算法对粗糙海面与舰船目标复合电磁散射研究是适用的,不仅能保证数值结果的计算精度,同时又能显著地提高计算效率,进一步体现出混合算法在时域快速计算中的优势.

2 海面与舰船目标复合散射的TDIETDKA混合算法

图1给出了一维海面与舰船目标复合电磁散射模型.如图1所示,瞬态电磁脉冲以入射角θi照射,与入射方向相反的方向称之为后向散射方向,与Y轴对称的方向称为镜向散射方向.将舰船及其邻近的海面划分为TDIE区域,将剩余的海面划分为TDKA区域.在计算海面与舰船目标复合电磁散射时,仅在舰船及邻近的海面用精确的TDIE方法求解,而对电大尺寸粗糙海面则采用高效的TDKA方法求解.

对于TE极化的入射波,磁感应强度垂直于XY平面(即沿着Z轴方向),因而散射模型表面S的电流密度J(r,t)沿着复合模型轮廓的切线方向.假定将TDIE区域分为N段,TDKA区域分为K段,用Rao-Wilton-Glisson基函数f(r)对TDIE区域表面电流JIE(r,t)和TDKA区域表面电流JKA(r,t)做近似展开[18],则有

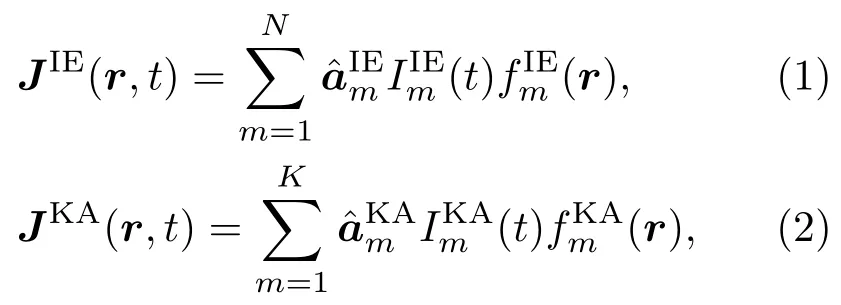
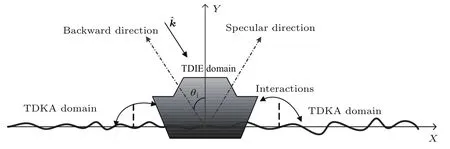
图1 海面与舰船目标复合电磁散射建模Fig.1.Geometric model for composite electromagnetic scattering from a ship located on sea surface.

其中LE为电场算子.在TE波入射下,电场算子LE对表面S的电流密度J(r,t)作用,定义如下:

将电流密度展开(1)和(2)式代入方程(4)和(6),在第j个时间步,即tj=j∆t时刻,在TDIE区域内对方程(4)做伽略金检验(试函数等于基函数),对方程(6)在TDKA区域内做伽略金检验,可得TDIE-TDKA混合算法的矩阵方程:

式中,

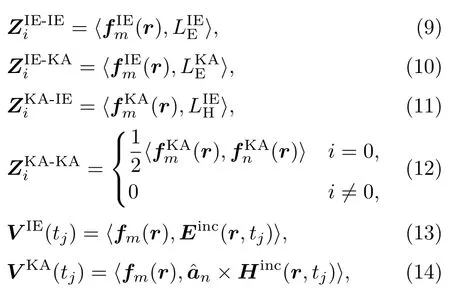
基于矩阵方程(8)的TDIE-TDKA时域步进混合算法,该算法在TDIE区域利用TD-EFIE精确求解,在TDKA区域利用TDKA电流近似计算.TDKA电流近似实际上忽略了TDKA区域内部电流相互作用,这极大地节省了电大尺寸的TDKA区域巨大的阻抗矩阵计算量,这是保障TDIE-TDKA时域步进混合算法高效率的关键.

3 数值计算结果与讨论

3.1 入射波及其参数设置

在分析粗糙面与目标复合散射问题时,常常采用一定能量宽度分布的锥形波照射,此时只需要计算有限大的粗糙面来模拟无限大粗糙面散射.在本文时域算法中,采用TE极化调制的高斯锥形脉冲波,其形式如下:

式中,

是窗函数[7],其中,ˆx表示沿着X轴正方向的单位矢量,g是入射波的锥形波因子,L是选取的粗面长度,x0是粗糙面的中心点;f0是调制脉冲波的中心频率;是沿着入射波传播方向的单位矢量,fbw是调制脉冲信号的带宽.表达式(16)是在原有调制高斯平面波的基础上,采用了加窗锥形波,它近似满足电磁波波动方程.当x远离粗糙面的中心点x0时,入射波的强度迅速衰减到零.

在下面所有数值算例中,TE调制的高斯锥形脉冲入射波采用如下参数:中心频率f0=375 MHz,带宽fbw=450 MHz,锥形波因子g=5.4,时间步长c∆t=0.02 LM(LM表示电磁波在真空中传播1.0 m所用的时间).

3.2 海面与舰船模型几何参数

图2 舰船目标模型参数Fig.2.Geometry of the ship-like target.

如图2所示,在下面的数值计算中,随机粗糙面采用一维“Pierson-Moskowitz”导体海面[21],被分成512段,沿着X轴方向每间隔0.05 m取一段,海面总长L=25.6 m,海面高度起伏受海面上方19.5 m处风速U19.5调控,风速越大,海面起伏越剧烈;取30个粗糙面样本,求平均值得最终数值结果.舰船目标尺寸参数用l量度,表示舰船目标吃水深度.

3.3 数值算法验证

为了验证混合算法在研究海面与舰船目标复合散射计算中的高效性和正确性,我们将混合算法的计算时间与传统TDIE算法[7]进行了对比.海面上方风速U19.5=2.0 m/s,舰船目标的尺寸参数l=0.05 m.可以通过调整TDIE区域的大小来调控混合算法的计算时间与计算精度.TDIE区域的划分采用以下三种方案:

1)取舰船目标及其近邻区域共长3.2 m为TDIE区域,其余部分为TDKA区域,此时未知量的数目为46;

2)取舰船目标及其近邻区域共长6.4 m为TDIE区域,其余部分为TDKA区域,此时未知量的数目为80;

3)将舰船目标及海面都取为TDIE区域,此时是传统的TDIE算法,未知量的数目是528.

利用Fortran6.5软件进行数值计算,混合算法在主频为2.93 GHz的Intel处理器(Intel(R)Core(TM)i3 CPU)、内存为4 GB、操作系统是Windows 7的计算机上进行.表1列出了在1000个时间步混合算法与传统TDIE算法计算时间的对比.由表1可以看出,混合算法与传统TDIE算法相比较,计算速度显著提升.此外,混合算法的计算时间随着TDIE区域未知量数目的增大而增加,并且都小于传统TDIE算法计算时间.当TDIE区域未知量数目为46时,混合算法的计算时间仅为传统TDIE算法计算时间的14.8%.

表1 TDIE-TDKA混合算法与传统TDIE算法在1000个时间步的计算时间Table 1.Computational time of the hybrid TDIETDKA and full TDIE method for 1000 time steps.

图3给出了当入射角为30◦,TDIE区域未知量数目为46时,舰船目标与海面复合模型的后向散射磁场(图3(a))、镜向散射磁场(图3(b)).可以看出,TDIE-TDKA混合算法与传统TDIE算法计算结果具有很好的一致性,说明TDIE-TDKA混合算法对于海面与舰船目标复合瞬态散射的计算是精确有效的.TDIE区域大小对于数值计算的精度和计算效率会有显著影响.如果TDIE区域划分过小,则影响计算结果的精度;如果TDIE区域划分过大,则影响数值计算的效率.通过数值计算结果可以发现,当选取TDIE区域中海面线度与舰船目标线度相当时,即可获得精确的数值结果.本算例中,舰船目标长度为1.2 m,选择的TDIE区域长度为3.2 m,舰船目标一侧领域海面长度约为1.1 m.舰船目标与近邻海面之间强耦合区域主要依赖于舰船目标本身的线度,当选取TDIE区域中海面线度与舰船目标本身线度相当时,TDIE-TDKA混合算法既能保证计算结果的精度,同时又能具有较高的计算效率.

图3 入射角为30◦时海面与舰船目标复合散射远场响应(a)后向散射磁场;(b)镜向散射磁场Fig.3.Far field responses of a ship located on sea surface for the incident angle (a)Backscattered magnetic field;(b)specularscattered magnetic field.

3.4 数值结果讨论

图4给出了当入射角为30◦、海面上方风速为U19.5=2.0 m/s时,海面上有、无舰船目标时的后向及镜像散射磁场.当海面上有舰船目标时,用TDIE-TDKA混合算法计算;当海面上无舰船目标时,用传统的TDIE算法计算.由图4可以看出,舰船目标对后向及镜向散射磁场均有影响,尤其是对后向散射磁场影响极大.因此,观测后向散射磁场的变化是雷达探测海面上方目标的关键.当海面上有舰船目标时,后向散射场急剧增大,这是由于舰船目标对电磁脉冲的强反射、舰船目标与海面之间多次复合散射耦合感应,使得后向散射磁场急剧增加,如图4(a)所示.海面与舰船目标之间的多次散射耦合感应,一方面会增强后向非相干散射,另一方面会削弱海面的相干散射.正是由于舰船目标造成海面的相干散射场削弱,导致海面与舰船目标镜像散射磁场比单纯海面镜像散射磁场有所减弱,如图4(b)所示.

图4 海面上有、无舰船目标时的远场响应 (a)后向散射磁场;(b)镜向散射磁场Fig.4.Far field responses of sea surface with or without a ship:(a)Backscattered magnetic field;(b)specularscattered magnetic field.

鉴于后向散射磁场对海面上方目标探测的重要性,图5给出了入射角为30◦时,海面上方不同风速下,海面与舰船目标后向复合散射磁场响应.当U19.5=0.2 m/s时,海面几乎是一个平面,当U19.5=2.0 m/s时,海面起伏显著增加.由图5可以看出,风速对复合模型后向瞬态散射磁场的影响并不显著.随着风速的增加,后向瞬态散射磁场略有增加,这是由于随风速的增加海面起伏增加,海面与舰船目标之间的耦合感应增强,从而使后向瞬态散射磁场加强.

接下来讨论电磁脉冲在不同角度入射时,海面与舰船目标后向散射磁场变化情况.从图6可以看出,入射角由30◦度增加到45◦,后向散射磁场增强,这说明海面与舰船目标之间存在的多次耦合散射在入射角为45◦时较强.后向散射磁场增强是由于海面与舰船目标之间形成了类似于二面角一样的反射器结构,使电磁脉冲在入射角为45◦时的后向散射磁场增强,类似的结果在文献[22]中也有报道.

由图6可知,与在30◦入射时的后向散射磁场相比,入射角为45◦时后向散射磁场增强,因此电磁脉冲在45◦入射时,复合模型参数的变化对后向散射磁场影响会更加显著.图7给出了电磁脉冲在45◦入射时,不同吃水深度的舰船目标对复合模型后向散射磁场的影响.由图7可以看出,舰船目标的吃水深度越大,后向散射磁场就越弱.这是由于海面与舰船目标复合模型后向散射磁场主要依赖于海面上方目标的大小,吃水深度越大,舰船目标在海面上方的部分就越小,海面与舰船目标之间的多次耦合散射减弱,这就使得后向散射磁场减弱.

图8给出了不同尺寸舰船目标对后向散射磁场的影响.由图8可以看出,舰船目标尺寸越大,后向散射磁场强度略有增加.舰船目标尺寸增加,海面与舰船目标之间多次耦合散射增强,从而使后向散射磁场增强.然而,舰船目标尺寸增加的同时也会增大舰船目标顶部平台的面积,舰船目标顶部平台面积的增加会导致镜像方向的强反射,这使得后向散射磁场减弱.在这两种散射机制的共同作用下,舰船目标尺寸的增加使后向散射磁场加强,但变化不是十分明显.

图6 入射角对后向散射磁场的影响 Fig.6.Backscattered magnetic field responses for different incident angle:(a)

图7 舰船目标的吃水深度对后向散射磁场的影响Fig.7.Backscattered magnetic field responses for different depth d of the ship immersing in sea surface.

图8 舰船目标尺寸对后向散射磁场远场的影响Fig.8.Backscattered magnetic field responses for different size of ship.

4 结 论

本文将TDIE-TDKA混合算法应用于粗糙海面与舰船目标复合电磁散射问题的研究中.该方法将粗糙海面与舰船目标复合模型划分为TDIE和TDKA区域.舰船目标及其近邻海面为TDIE区域,剩余电大尺寸的粗糙海面为TDKA区域,求解过程中考虑了两个区域表面电流的相互耦合作用.与传统的TDIE算法相比较,混合算法能在提高计算效率的同时兼顾数值计算的精度.数值结果表明,海面上无舰船目标时,后向散射磁场急剧减小,镜像散射磁场略有增强且变化不大.因此,后向散射远场是海面上方舰船目标探测的基础.此外,利用混合方法研究了海面上方风速、电磁脉冲入射角、舰船目标尺寸、吃水深度对后向瞬态散射磁场的影响,研究结果对于海面上方舰船目标探测、海洋遥感和目标识别等领域具有一些参考价值.本文将TDIE-TDKA混合算法应用于一维粗糙海面与二维舰船目标的复合散射,拓展了混合算法的应用范围.对于更为实际的二维粗糙海面与三维舰船目标的复合瞬态散射混合算法的研究,将是我们下一步工作的重点.

[1]Holliday D 1987IEEE Trans.Antennas Propag.35 120

[2]Voronovich A 1994Waves Random Media4 337

[3]Winebrenner D,Ishimaru A 1985Radio Sci.20 161

[4]Lentz R R 1974Radio Sci.9 1139

[5]Xu R W,Guo L X,Fan T Q 2013Acta Phys.Sin.62 170301(in Chinese)[徐润汶,郭立新,范天奇2013物理学报62 170301]

[6]Li J,Guo L X,Zeng H 2008Waves Random Media18 641

[7]Wang R,Guo L X,Li J,Liu X Y 2009Sci.China G:Phys.Mech.Astron.52 665

[8]Wang R,Guo L X,Ma J,Wu Z S 2009Chin.Phys.B18 1503

[9]He S Y,Zhu G Q 2007Microw.Opt.Technol.Lett.49 2957

[10]Li J,Guo L X,He Q 2011Electron.Lett.47 1147

[11]Qin S T,Guo L X,Dai S Y,Gong S X 2011Acta Phys.Sin.60 074217(in Chinese)[秦三团,郭立新,代少玉,龚书喜2011物理学报60 074217]

[12]Li J,Guo L X,Jiao Y C,Li K 2011Opt.Express19 1091

[13]Yang L X,Ge D B,Wei B 2007Prog.Electromagn.Res.76 275

[14]Walker S P,Vartiainen M J 1998IEEE Trans.Antennas Propag.46 318

[15]Ren M,Zhou D M,Li Y,He J G 2008Electron.Lett.44 258

[16]Qin Y,Zhou D,He J,Liu P 2009Prog.Electromagn.Res.M8 153

[17]Qin S T,Gong S X,Wang R,Guo L X 2010Prog.Electromagn.Res.102 181

[18]Vechinski D A,Rao S M 1992IEEE Trans.Antennas Propag.40 1103

[19]Rao S M,Wilton D R 1991IEEE Trans.Antennas Propag.39 56

[20]Vechinski D A,Rao S M 1992IEEE Trans.Antennas Propag.40 661

[21]Kuga Y,Phu P 1996Prog.Electromagn.Res.14 37

[22]Li J,Wei B,He Q,Guo L X,Ge D B 2011Prog.Electromagn.Res.121 391

Composite electromagnetic scattering from a ship located on one-dimensional sea surface with time-domain hybrid method∗

Wang Qiang1)2)Guo Li-Xin1)†

1)(School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China)
2)(Department of Computer and Electronic Information,Shaanxi Xueqian Normal University,Xi’an 710100,China)

4 April 2017;revised manuscript

3 June 2017)

With the development of broadband radar technology,transient composite scattering from a target and a randomly rough surface has aroused a great interest in oceanic remote sensing,target identification,and military applications.Time-domain integral equation(TDIE)is an effective numerical method of analyzing transient and broadband electromagnetic problems.However,the high computational complexity of numerical methods restricts its applications in analyzing the electrically large rough surfaces.To improve computational efficiency,hybrid methods have been developed by combining an analytical method with a numerical algorithm,and used to solve the electromagnetic scattering of a composite model.In these hybrid methods,numerical methods are used to calculate the scattering from a target,and analytical methods are employed to solve the scattering from a rough surface.To our knowledge,most of the hybrid methods for composite electromagnetic scattering are frequency-domain algorithms and used to investigate composite scattering from a rough surface with a target above it.Few papers have been published on the analysis of transient scattering from a rough surface with a target by using the time-domain hybrid methods.In the present paper,an efficient time-domain hybrid method that combines time-domain Kirchho ffapproximation(TDKA)with TDIE is first designed to investigate the transient electromagnetic scattering from a ship located on a randomly rough sea surface.In this hybrid method,the ship and its adjacent sea surface are chosen as TDIE region and the rest of the rough surface is TDKA region.Considering the interactions between the TDIE region and the TDKA region,the hybrid TDIE-TDKA formula is derived and solved with an iterated marching-on-in-time method.Initially,the induced currents of the TDIE region are acquired by solving TDIE.Then,the currents in the TDKA region are obtained via TDKA method.The interactions between the currents in the TDKA region are neglected.The efficiency and accuracy of the hybrid TDIE-TDKA method depend on the size of the TDIE region.The minimum length of sea surface in the TDIE region is at least the size of the ship due to the strong interactions between the ship and its adjacent sea surface.Numerical results show that the hybrid TDIE-TDKA method presented in this paper is accurate and efficient compared with the full TDIE.Moreover,the in fluences of the ship size,the wind speed,the incident angle,and the depth of the ship immersing in sea surface on the backscattered far magnetic field are discussed in detail.

rough sea surface,hybrid method,time-domain integral equation,transient electromagnetic scattering

PACS:03.50.De,41.20.–q,43.20.PxDOI:10.7498/aps.66.180301

*Project supported by the Foundation for Innovative Research Groups of the National Natural Science Foundation of China(Grant No.61621005),the National Natural Science Foundation of China(Grant No.61431010),and the Scientific Research Program Funded by Shaanxi Provincial Education Department,China(Grant No.15JK1180).

†Corresponding author.E-mail:lxguo@xidian.edu.cn

(2017年4月4日收到;2017年6月3日收到修改稿)

采用时域积分方程(TDIE)与时域基尔霍夫近似(TDKA)的混合算法研究粗糙海面与舰船目标的复合瞬态电磁散射.该方法将舰船目标及其近邻海面划分为TDIE区域,用TDIE方法精确求解;将剩余电大尺寸的粗糙海面划分为TDKA区域,采用高效的TDKA电流近似求解.通过混合算法和传统TDIE算法结果的对比,表明TDIE-TDKA混合算法能保证计算的精度,同时具有较高的计算效率.最后,讨论了海面上方有无目标、海面上方风速、电磁脉冲入射角、舰船目标尺寸、吃水深度对后向散射磁场的影响.

10.7498/aps.66.180301

∗国家自然科学基金创新研究群体科学基金(批准号:61621005)、国家自然科学基金重点项目(批准号:61431010)和陕西省教育厅科学研究计划项目(批准号:15JK1180)资助的课题.

†通信作者.E-mail:lxguo@xidian.edu.cn