横场中具有周期性各向异性的一维XY模型的量子相变∗
宋加丽 钟鸣 童培庆2)
1)(南京师范大学物理科学与技术学院,南京 210023)
2)(江苏省大规模复杂系统数值模拟重点实验室,南京 210023)
横场中具有周期性各向异性的一维XY模型的量子相变∗
宋加丽1)钟鸣1)†童培庆1)2)‡
1)(南京师范大学物理科学与技术学院,南京 210023)
2)(江苏省大规模复杂系统数值模拟重点实验室,南京 210023)
周期性各向异性XY模型,量子相变,各向同性铁磁相,冯·诺依曼熵
1 引 言
低维量子系统是人们用来了解量子关联的一个重要模型,其中一维自旋模型得到广泛研究.一方面,此类模型相对比较简单,可以通过解析和数值方法深入理解它们的性质,有助于预测和解释其他复杂模型的相关性质,并且某些自旋模型还可直接用来解释很多实验上的物理现象[1,2].另一方面,复杂模型可以借助一些方法映射到此类简单模型,比如一些绝缘化合物可以看作是相互独立的自旋单链的集合,这样将模型简单化,只需研究单链就能得到很多重要的物理信息[3].此外一维自旋模型在生命科学[4−6]、金融经济[7]等领域也有着重要的应用.
众多一维自旋模型中研究最多的是横场中各向异性XY模型.这类简单且具有广泛代表性的模型大多是精确可解的[8,9].目前,关于XY自旋模型,人们除了在理论上取得了很多丰硕的成果,在实验上也已经能制备出一些与理论描述符合得很好的样品[10,11].几十年来,人们从多个角度对这类模型的物理性质进行了非常深入的研究,其中讨论得最多的性质之一就是零温下的量子相变.当改变一个自旋系统的某些参数时,相变就有可能产生.研究表明均匀的XY模型存在两种类型的量子相变,分别是Ising相变[12]和各向异性相变[13].目前,人们用来研究自旋系统量子相变性质的方法有很多.一般情况下,我们会借助一些序参量,如磁矩、磁化率和自旋关联函数来描述量子相变.随着量子信息、量子通信等领域的发展,一些方法和概念,如量子纠缠[14−16]、量子失协[17−19]、保真度[20,21]也被用来描述量子相变.人们发现均匀XY模型的量子纠缠与量子相变有关:相变点处的纠缠行为与子链长的对数呈线性关系,但在Ising相变和各向异性相变情况下对数前系数是不一样的[14,15].
上述这些模型基本上都是均匀的,但在自然界中存在着大量非均匀(周期、准周期、无序等)的系统.所以,无序和准均匀结构对模型相变的影响一直是统计物理和凝聚态物理领域中研究的热点.人们通过重整化群的方法研究了无序对Ising相变和各向异性相变的影响,发现无序改变了系统相变的普适类[22,23].1993年,Luck[24]指出两类准周期结构对横场中Ising链的量子相变的影响是不同的,第一类准周期结构不改变系统量子相变的普适类;第二类准周期Ising链的量子相变的普适类与无序链的相同.但是,最近张振俊等[25]的工作表明第二类准周期结构的自旋链量子相变与无序情况是有区别的.为了解释以上问题,人们对周期性结构的自旋模型的量子相变做了大量的研究,例如横场中具有周期性最近邻相互作用的XY模型[26−29],发现模型的最近邻交换相互作用周期地取不同值时,相对于均匀XY模型,系统会出现更多的相变点.在这些模型中主要研究了周期性交换相互作用对系统量子相变的影响,但不同格点的各向异性参数都是一样的.本文研究周期性各向异性参数对系统量子相变的影响.发现当周期为二且两个各向异性参数值之比α=−1时,系统会出现新的相.
2 模型和公式
考虑一个一维均匀横场中各向异性XY模型(N个格点),其哈密顿量为
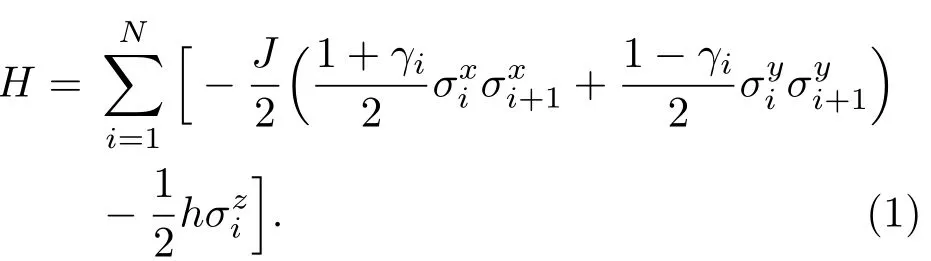
通过Jordan-Wigner变换[12],系统哈密顿量可以改写成如下无自旋费米子形式:

矩阵A和B的非零元素为本文只考虑N为偶数的情况,因此取反周期性边界条件[26],即不失一般性,取J=1.
再应用Bogoliubov变换,得到对角化的哈密顿量:

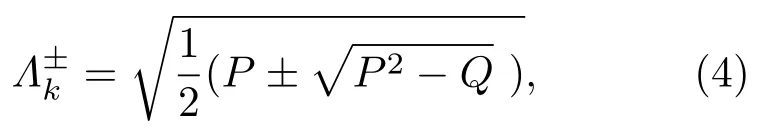
其中,

在本模型中Λk总是非负的,所以根据方程(3),系统基态能量写为

系统基态和第一激发态之间的能隙∆=min{Λ−k},其对应的波矢k0满足
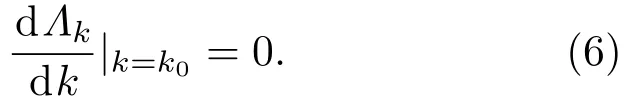
当∆=0,系统第一激发态与基态之间没有能隙.随着参数的变化,如果∆由非零值变为零,说明系统发生了相变;如果∆一直是零值,则说明系统处在一个无能隙的状态.
2.1 关联函数
选取两格点的长程关联函数作为序参量来描述系统的相变行为.其定义为
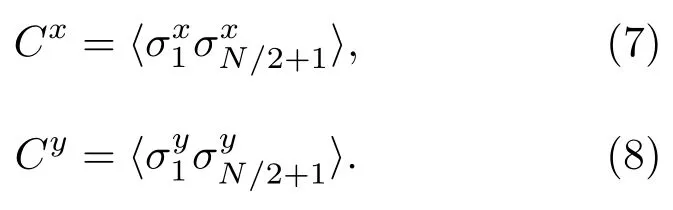
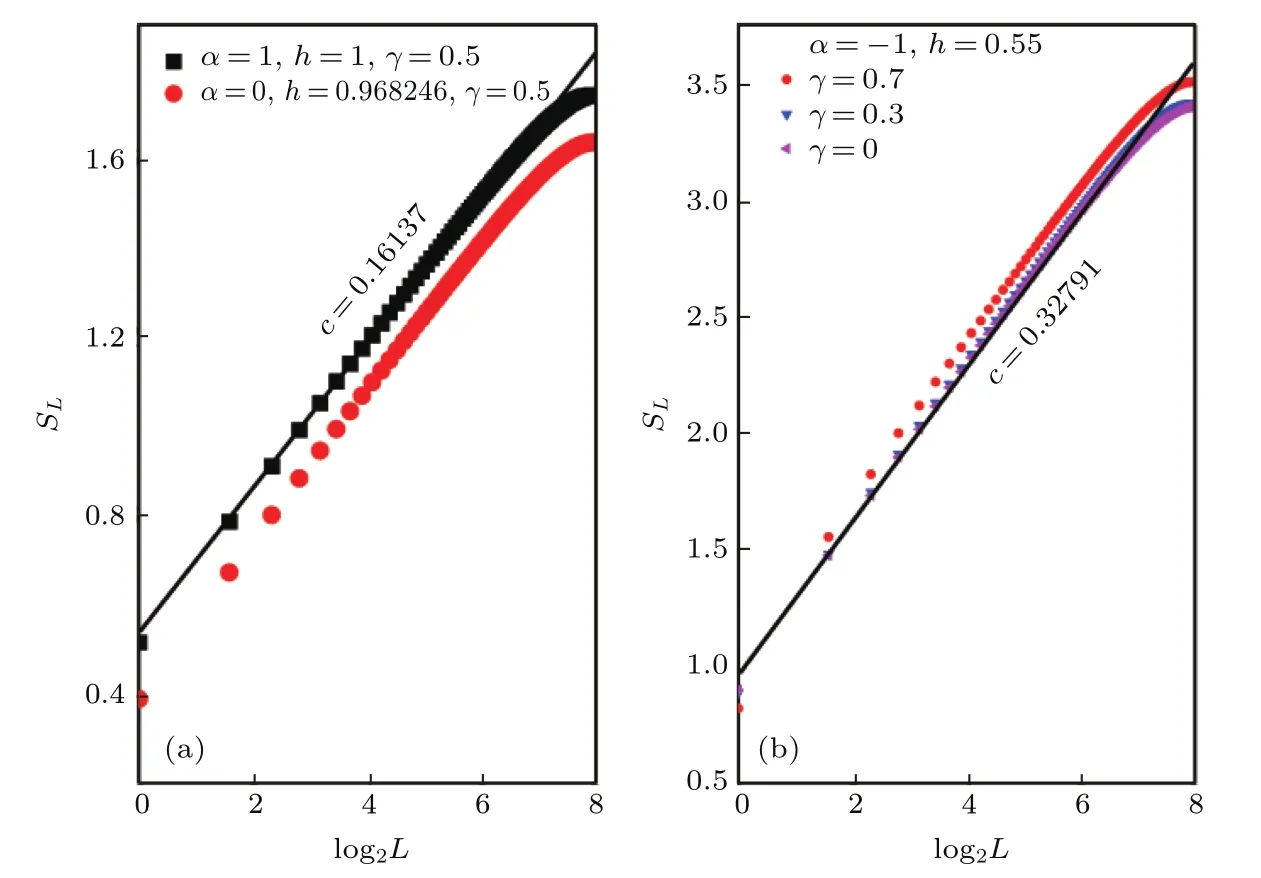
Lieb等[12]给出了两格点关联函数的计算方法.通常把Cx=Cy=0的相叫作顺磁(PM)相;把Cx>Cy>0的相叫作沿x方向的铁磁有序(FMx)相;把0 6Cx 对于一维自旋模型块与块之间的量子纠缠的研究,冯·诺依曼熵是一个非常重要的物理量.所以本文采用冯·诺依曼熵来研究一维各向异性XY模型的量子纠缠.当由两个子系统A,B构成的系统处于态|ΨAB⟩时,其冯·诺依曼熵(又叫部分纠缠熵)的定义为 其中约化密度矩阵 设子系统A有L个连续自旋,其冯·诺依曼熵在非相变点区域是常数[15],而在相变点附近存在着奇异性: 对于均匀各向异性XY模型,在Ising相变点处系数c=1/6;在各向异性相变点处系数c=1/3. 系统发生相变时,第一激发态和基态之间的能隙为零,所以我们可以通过计算单粒子能谱最小值∆=0来确定可能的对应相变的点.得到的解析结果如下. 1)当γ=0时,系统对应的是横场中各向同性XY模型.因此,横场h∈[0,1]所对应的系统是无能隙的. 2)当α≠且γ≠0时,系统在 处的∆为零,而在其他h处∆均大于零,如图1所示.图1(a)和图1(b)分别对应α=1,0时不同h情况下系统的单粒子能谱(不失一般性,取γ=0.5).这说明系统在hc1点发生了相变. 特别地,当α=1时,系统就变成了均匀XY模型,对于这种模型的量子相变,我们已经取得了很多丰富的成果[15,30,31].因此,从计算结果及能谱图可以看出,α≠1时模型的相变行为与均匀XY模型相似,只是相变点位置发生了变化. 图1 (网刊彩色)α取不同值时,横场中各向异性参数周期为二的一维XY模型不同区域的单粒子能谱 (a)α=1;(b)α=0;(c)α=−1;γ=0.5,N=500Fig.1.(color line)The single particle energy spectra of the period-two anisotropic XY chains in a transverse field with different α for:(a)α =1;(b)α =0;(c)α = −1.Here γ =0.5,N=500. 3)当α=−1时,系统在 处的能隙∆为零.图1(c)给出了此种情形下不同h所对应的系统的单粒子能谱.从图1(c)我们可以发现,当时,单粒子能谱总有两个零点,对应着一个无能隙的相;当时能隙∆均大于零.因此,系统的相变临界线为 很明显,α≠1和α=−1对应的模型的相和相变行为是不一样的.尤其是α=−1时系统出现了一个无能隙的相,这值得我们进一步研究,以确定相应的相图及系统纠缠熵的标度行为. 图2给出了参数α取不同值时,XY模型的Cx,Cy关于h和γ的函数变化情况,不失一般性地取α=1,0,−1.图2(a)和图2(b)表示α=1的情况,即横场中均匀XY模型,可以看到随着h(不失一般性取γ=0.5)的增大,系统由FMx(Cx>Cy)相变为PM(Cx=Cy=0)相,相变点为hc=1,对应的是Ising相变;当0 图2 (网刊彩色)α取不同值时,横场中各向异性参数周期为二的一维XY模型的长程关联函数分别关于h和γ的变化情况 (a),(b)对应α=1的情形;(c),(d)对应α=0的情形;(e),(f)对应α=−1的情形Fig.2.(color line)The long-range correlations of the period-two anisotropic XY chains in a transverse field with different α as functions of γ and h for:(a),(b)α =1;(c),(d)α =0;(e),(f)α = −1. 图2(e)和图2(f)给出的是α=−1时系统的Cx和Cy关于h和γ的变化曲线.随着外场h增大,Cx,Cy同时由大于零的值变为零,系统由有序相过渡到无序相.其相变发生位置为与解析计算得到的结果完全一致.在h>hc2区域内Cx=Cy=0,系统所处的相仍然是PM相;而在h 为了了解FMxx相出现的原因,我们分析了系统的对称性,发现当α=−1时模型的哈密顿量在经过变换之后保持不变.为此我们计算了最相邻格点的关联函数随外场h的变化曲线,如图3所示.结果显示第2i−1和2i格点间沿x(y)方向的关联函数等于第2i和2i+1格点间沿y(x)方向的关联函数,因而导致了不同方向的长程关联函数相等.正是存在这样的对称性,系统在h 在参数α不同的情况下,通过研究Cx,Cy关于h和γ的函数行为,发现数值结果与前文中求出的解析式(11)和(13)相一致.于是,我们得到了系统在不同α取值情况下参数空间(h,γ)中的相图,如图4所示. 图3 (网刊彩色)α=−1时,横场中各向异性参数周期为二的一维XY模型最近邻格点关联函数随外场h的变化(a)实线、短划线分别对应(b)实线、短划线分别对应γ =0.5,N=500Fig.3.(color line)The short-range correlations of the period-two anisotropic XY spin models in a transverse field with α = −1 as functions of h for:(a)The solid and dashed lines correspond to (b)the solid and dashed lines correspond to γ =0.5,N=500. 图4 (网刊彩色)横场中各向异性参数周期为二的一维XY模型的相图 (a)α=1,0;(b)α=−1Fig.4.(color line)Phase diagram of the period-two anisotropic XY chains in a transverse field for:(a)α=1,α=0;(b)α=−1. 对于横场中均匀XY模型,系统的冯·诺依曼熵在Ising相变和各向异性相变处与子链长的对数存在线性关系[15],但是在沿x(y)方向的各向异性铁磁(FMx,FMy)相和PM相内会很快收敛到一个常数值.这三个相都是有能隙的,而当α=−1时系统出现了一个无能隙的铁磁(FMxx)相.因此,我们借助冯·诺依曼熵进一步数值研究了不同α情形下系统的量子纠缠行为. 我们发现当α≠1(图5(a))时系统在相变点h=hc1附近的SL变化曲线和横场中均匀XY模型(α=1)在Ising相变点处的纠缠行为相似,即与子链长L的对数呈线性关系,对数前系数为1/6.图5(b)显示的是当α=−1时系统在FMxx相内某点(不失一般性取h=0.55;γ=0.7,0.3,0)的冯·诺依曼熵SL随log2L变化的曲线图.与均匀XY模型的纠缠行为不同,结果表明在FMxx相内SL也随着子链长的对数log2L的增加而线性增长,且对数前系数c=1/3,这与横场中均匀XY模型在各向异性相变点处的纠缠行为(图中上三角曲线)相似.通过之前的分析可知,横场中处在FMxx相上的XY模型和均匀XY模型在各向异性相变点处的单粒子能谱都有两个取值不为零和±π/2的k0使∆=0,因此FMxx相内系统的冯·诺依曼熵与均匀XY模型在各向异性相变点处的纠缠行为相似. 图5 (网刊彩色)横场中各向异性参数周期为二的一维XY模型的冯·诺依曼熵随子链长L的变化 (a)h=1,γ=0.5,α=1;h=0.968246,γ =0.5,α =0;(b)α = −1,h=0.55,γ =0.7,0.3,0Fig.5.(color line)SLof the period-two anisotropic XY chains in a transverse field of the system in the FMxx phase as functions of L(the size of the subsystem)for:(a)h=1,γ =0.5,α =1;h=0.968246,γ =0.5,α =0;(b)α=−1,h=0.55,γ=0.7,0.3,0. 本文讨论了横场中具有周期性各向异性参数的一维XY模型的量子相变和量子纠缠.数值计算了两格点长程关联函数Cx,Cy,发现当α≠1时,系统的相变行为与横场中均匀XY模型的相似;而当α=−1时系统在h [1]Suzuki S,Inoue J I,Chakrabarti B K 2013Quantum Ising Phases and Transitions in Transverse Ising Models(Berlin:Springer-Verlag)p13 [2]de Gennes P G 1963Solid State Commun.1 132 [3]Bitko D,Rosenbaum T F,Aeppli G 1996Phys.Rev.Lett.77 940 [4]Vtyurina N N,Dulin D,Docter M W,Meyer A S,Dekker N H,Abbondanzieri E A 2016Proc.Nat.Acad.Sci.USA113 4982 [5]Fan B,Branch R W,Nicolau D V,Pilizota T,Steel B C,Maini P K,Berry R M 2010Science327 685 [6]Shi Y,Duke T 1998Phys.Rev.E58 6399 [7]Sornette D 2014 arXiv:1404.0243v1[q- fin.GN] [8]Jin B Q,Korepin V E 2004I.Stat.Phys.116 79 [9]Islói F,Juhász R 2008Europhys.Lett.81 57003 [10]Babkevich P,Jeong M,Matsumoto Y,Kovacevic I,Finco A,Toft-Petersen R,Ritter C,Månsson M,Nakatsuji S,Rønnow H M 2016Phys.Rev.Lett.116 197202 [11]Kenzelmann M,Coldea R,Tennant D A,Visser D,Hofmann M,Smeibidl P,Tylczynski Z 2002Phys.Rev.B65 144432 [12]Lieb E,Schultz T,Mattis D 1961Ann.Phys.NY16 407 [13]Pfeuty P 1970Ann.Phys.NY57 79 [14]Osterloh A,Amieo L,Falci G,Fazio R 2002Nature416 608 [15]Vidal G,Latorre J I,Rico E,Kitaev A 2003Phys.Rev.Lett.90 227902 [16]Franchini F,Its A R,Korepin V E 2008J.Phys.A:Math.Theor.41 025302 [17]Raoul D 2008Phys.Rev.B78 224413 [18]Guo J L,Wei J L,Qin W,Mu Q X 2015Quantum Int.Process14 1429 [19]Cheng W W,Li J X,Shan C J,Gong L Y,Zhao S M 2015Quantum Int.Process14 2535 [20]Zanardi P,Paunkovic N 2006Phys.Rev.E74 031123 [21]Quan H T,Song Z,Liu X F,Zanardi P,Sun C P 2006Phys.Rev.Lett.96 140604 [22]Fisher D 1994Phys.Rev.B50 3799 [23]Bunder J,McKenzie R 1999Phys.Rev.B60 344 [24]Luck J M 1993J.Stat.Phys.72 417 [25]Zhang Z J,Li W J,Zhu X,Xiong Y,Tong P Q 2015Acta Phys.Sin.64 190501(in Chinese)[张振俊,李文娟,朱璇,熊烨,童培庆2015物理学报64 190501] [26]Tong P Q,Zhong M 2001Physica B304 91 [27]Zhong M,Tong P Q 2010J.Phys.A:Math.Theor.43 505302 [28]Tong P Q,Liu X X 2006Phys.Rev.Lett.97 017201 [29]Zhong M,Liu X X,Tong P Q 2007Int.J.Mod.Phys.B21 4225 [30]Latorre J I,Rico E,Vidal G 2004Quantum Int.Comput.4 48 [31]Sachdev S 2011Quantum Phase Transitions(Cambridge:Cambridge University Press)p133 Quantum phase transitions of one-dimensional period-two anisotropicXYmodels in a transverse field∗ Song Jia-Li1)Zhong Ming1)†Tong Pei-Qing1)2)‡ 1)(Department of Physics and Institute of Theoretical Physics,Nanjing Normal University,Nanjing 210023,China) 2)(Jiangsu Key Laboratory for Numerical Simulation of Large Scale Complex Systems,Nanjing Normal University,Nanjing 210023,China) 18 February 2017;revised manuscript 18 May 2017) The quantum phase transitions of one-dimensional period-two anisotropicXYmodels in a transverse field with the Hamiltonian where the anisotropy parametersγitakeγandαγalternately,are studied.The Hamiltonian can be reduced to the diagonal form by Jordan-Wigner and Bogoliubov transformations.The long-range correlationsCxandCyare calculated numerically.The phase withCx>Cy̸=0(orCy>Cx̸=0)is referred to as the ferromagnetic(FM)phase along thex(ory)direction,while the phase withCx=Cy=0 is the paramagnetic(PM)phase.It is found that the phase diagrams with the ratioα≠1 andα=−1 are different obviously. For the case withα≠1,the lineseparates an FM phase from a PM phase,while the lineγ=0 is the boundary between a ferromagnetic phase along thexdirection(FMx)and a ferromagnetic phase along theydirection(FMy).These are similar to those of the uniformXYchains in a transverse field(i.e.,√α=1).Whenα=−1,the FMxand FMyphases disappear and there appears a new FM phase.The lineh=hc2= 1− γ2separates this new FM phase from the PM phase.The new phase is gapless with two zeros in single particle energy spectrum.This is due to the new symmetry in the system withα=−1,i.e.,the Hamiltonian is invariant under the transformationσ2xi→σ2yi+1,σ2yi→σ2xi+1.The correlation function between the 2i−1 and 2ilattice points along thex(y)direction is equal to that between the 2iand 2i+1 lattice points along they(x)direction.As a result,the long-range correlation functions along two directions are equivalent.In order to facilitate the description,we call this gapless phase the isotropic ferromagnetic(FMxx)phase. Finally,the relationship between quantum entanglement and quantum phase transitions of 1 the system is studied.The scaling behaviour of the von Neumann entropy at each point in the FMxxphase isSL∼3log2L+Const,which is similar to that at the anisotropic phase transition point of the uniformXYmodel in a transverse field,and different from those in the FMxand FMyphases. period-two anisotropicXYmodel,quantum phase transition,isotropic ferromagnetic phase,von Neumann entropy PACS:03.65.–w,75.10.Pq,75.50.Gg,68.65.–kDOI:10.7498/aps.66.180302 *Project supported by the National Natural Science Foundation of China(Grant No.11575087). †Corresponding author.E-mail:mzhong@njnu.edu.cn ‡Corresponding author.E-mail:pqtong@njnu.edu.cn (2017年2月18日收到;2017年5月18日收到修改稿) 通过解析和数值计算的方法研究了横场中具有周期性各向异性的一维XY自旋模型的量子相变和量子纠缠.主要讨论了周期为二的情况,即各向异性参数交替地取比值为α的两个值.结果表明,与横场中均匀XY模型相比,α=−1所对应的模型在参数空间的相图存在着明显的不同.原来的Ising相变仍然存在,没有了沿x和y方向的各向异性铁磁(FMx,FMy)相,即各向异性相变消失,出现了一个新的相,并且该相内沿x和y方向的长程关联函数相等且大于零,我们称新相为各向同性铁磁(FMxx)相.这是由于系统新的对称性所导致的.解析结果还说明系统在FMxx相中的单粒子能谱有两个零点,是一个无能隙的相.最后,利用冯·诺依曼熵数值地研究了系统在新相内各点的量子纠缠,发现该相内每一点的冯·诺依曼熵的标度行为与均匀XY模型在各向异性相变处的相似,即 10.7498/aps.66.180302 ∗国家自然科学基金(批准号:11575087)资助的课题. †通信作者.E-mail:mzhong@njnu.edu.cn ‡通信作者.E-mail:pqtong@njnu.edu.cn2.2 冯·诺依曼熵


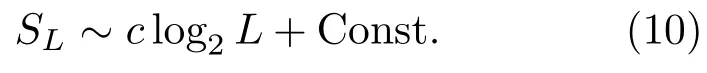
3 结果与讨论


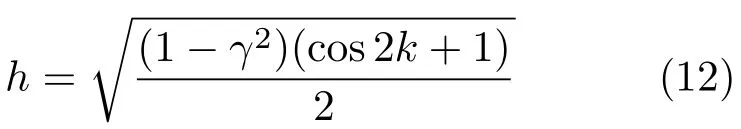

3.1 关联函数和相图



3.2 冯·诺依曼熵
4 结 论


