几何变换，策略教学——初中数学几何变换思想的教学策略的研究

江苏省泗阳致远中学 胡佃平

几何变换，策略教学
——初中数学几何变换思想的教学策略的研究

江苏省泗阳致远中学 胡佃平

一直以来，几何变换都是初中数学的重要思维方式之一，且作为课程改革所重点提及的内容，近年来，更是成为考试命题的热点内容。因此，作为初中数学教师，其在实际的教学过程中，应着重对学生的几何变换思维能力进行培养，为学生今后的学习奠定基础。

初中数学；几何变换；教学策略

所谓的变化思想，即将某种复杂的形式转变为另一种方便理解的形式的思想，是思维方式的一种。那么相应的，所谓的几何变换思想便是将相对复杂的几何图形转化为另一种便于理解的几何图形的思想。在初中数学中，几何变换思想主要运用在全等变换与相似变换两大方面，其对培养初中生的几何变换思想具有十分重要的意义。对此，作为初中数学教师，应给予足够的重视。

一、全等变换

全等变换是几何变换最常用的方法之一，由于变化后的图形与之前的图形是相等的，因而被称之为全等变换。当然，全等变换亦包括部分较为特殊的情况，如平移变换、旋转变换以及翻折变换，又称轴对称。以下为全等变换思想在几何问题中的具体应用。

1.平移变换

平移变换是全等变换中最常用的变换思想之一，其在几何图形中的运用通常是将该几何图形的各个顶点向与之平行的同一方向移动相同距离，而后通过连接平移后图形与原图形之间的对应点，从而达到简化问题的目的。针对平移变换，其主要包含如下性质：首先针对图形本身，其与平移前的图形两者的对应点分别在平移的线段中平行且相等，而与之相对应的线段亦在同一条直线上且相等。而在对应角方面，因其图形的形状与大小均未发生变化，因此对应角亦相等。通过平移变换，虽仅是改变了图形原本的位置，但通过平移，能将原本分散的条件集中到一起，继而方便了问题的解决。

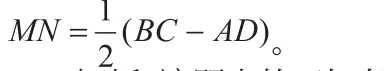
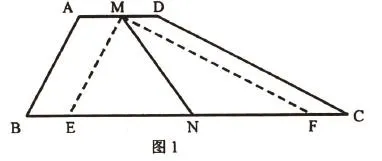
解析：该题中的已知条件MN、BC与AD原本处于较为分散的状态，且未集中于同一三角形中，加之AD与BC平行，因而可将AM、DM分别进行平移转换，以求出BC与AD之差，最后仅需证明MN为BC、AD差之一半即可。

2.旋转变换

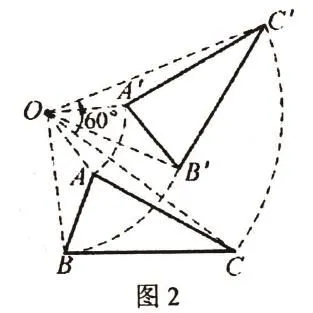
旋转变换在几何问题中的运用，如图2所示，该题首先将三角形ABC沿O点逆时针旋转至三角形A'B'C'的位置，图形旋转后，其每一点旋转的角度、对应线段以及图形形状与大小均相等。与平移变换的相同之处在于，两者均是通过集中问题的已知条件，以找出条件与结论之间的联系。

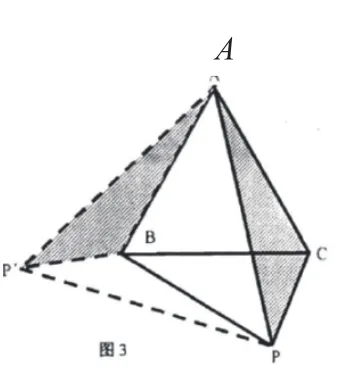
例2 如图3，P为等边三角形ABC外的一点，结合图形，尝试证明PA＜PB+PC。

解析：针对此类题型，最合理的解决方法便是采用旋转变化思想。首先，将三角形ACP沿A点顺时针旋转60°形成三角形ABP',根据平移变换性质可得AP=AP'，PC=PC'，∠PAP'=60°，由此可得△APP'为等边三角形，进而得出PP'=AP，依照三角形的三边关系可得PP'=BP+BP',继而可证PA＜PB+PC。

二、在初中几何教学中的教学策略

1.从学生熟悉的事物引入变换教学

学生在幼儿园及小学阶段进行过大量的如折纸、放风筝一类的游戏，而这些游戏与变换之间有着一定的联系。对此，在初中阶段进行几何变换教学时，教师便可以游戏的方式来讲解几何变化的集中类型，如此不仅能有效激发学生的学习兴趣，更能让学生体会到学习数学对实际生活的帮助。因此，通过引进学生所熟悉的事物来展开变换教学，将有利于学生理解。

例如，在进行“轴对称变换”的相关内容的教学时，教师便可引进这样的教学案例：首先，教师为学生播放故宫的视频，当学生看到宏伟而美丽的故宫时，将能促使学生注意力高度集中，此后，教师引导学生就故宫的特点进行观察，此时，学生发现故宫由中间“切开”，其左右两边呈现出对称的状态，进而由此展开轴对称变换的教学。其次，欣赏生活中丰富的实例(不同类别)，例如观看图片（如图3），看看有什么共同特点？

图3

通过为学生展示来自生活中的图片，能让学生在感受对称这一数学概念的同时，体会到生活中蕴藏的数学思想，继而感受到学习数学的重要性。最后，动手操作：印有半只蝴蝶图案的一张纸（如图4），你可以用什么办法把它补成一只完整的蝴蝶呢？

针对实际操作，学生首先想到的便是利用数学中的对称思想来完成。由此可见，利用实际生活中的事物，将能在潜移默化中影响学生，进而在无形中感受到轴对称图形的特点。

图4

2.加强元认知教学，培养学生主动学习

初中变换思想教学，其主要目的在于通过学习变换的思想来加深学生对初中数学知识的学习记忆，并促使学生积极将变换思想运用到实际生活中，以解决生活中的实际问题。与此同时，培养学生针对同一问题由不同角度去思考的习惯，以此提升学生的学习主动性。

例如，如图5，在菱形ABCD中，AB的中点为M，对角线AC上有一动点P，若PM与PB之和的最小值为3，那么AB的长为多少？

图5

归纳：该图形具有中心对称以及轴对称两大特点，因此针对上述问题，可分别采用中心对称变换与轴对称变换思想，以完善向实际问题的转化，或可设置相应的背景来解决问题。

总之，在初中数学课堂的教学过程中，采用几何变换思想教学策略，有利于指导学生将数形结合起来，促使学生深入学习数学知识，理解数学内容，从而有效提高初中数学课程的教学水平。

[1]胡荣萍.初中数学几何变换思想的教学策略的研究[D].四川师范大学，2013.

[2]王世平.初中数学几何变换思想的教学策略[J].新课程·中旬，2016（9）.