对数学课题活动开展现状的思考
江苏省南京市天景山中学 章利霞
对数学课题活动开展现状的思考
江苏省南京市天景山中学 章利霞
数学课程标准中提出“数学教学是数学课题活动的教学”,教师应“向学生提供充分从事数学活动的机会”,让学生在做中学、玩中学。数学课题活动有以下几方面需要努力:意识亟待培养、方法亟待指导、素材亟待挖掘,尤其从数学课题活动的素材挖掘方面谈了几个可能的途径,分别是:从定义中来;从定理讲解中来;从例题讲解中来;从实际生活中来。
数学课题活动;意识;方法;素材
一、意识亟待培养
现在的教材中,“课题学习”、“做一做”等内容所占比重较大,“做可能大的长方体”、“测量旗杆的高度”等内容,是重要的数学课题活动素材,但教学时间少,为完成教学计划及应付考试,好多教师不重视。开展适当的活动,让学生在不断地尝试——改进——再尝试中体验、感悟,其后再与他人交流、取长补短,增强学生的数学意识和学习态度,所以数学教师对进行数学课题活动的意识要亟待加强。
建构主义者认为:知识主要是学习者在一定的情境下,借助他人的帮助,利用必要的学习资源实现对知识的意义建构。开展好必要的活动让学生参与进来,激发他们学习数学的兴趣已刻不容缓。
二、方法亟待指导
有些教师将数学课题活动等同于数学实践活动,热闹的课堂静不下来,学生忙忙碌碌,或动手操作,或合作交流,缺少了学生独立思考的时间和机会,而教师却置身事外。这就对教师素质提出了更高的要求,驾驭能力、调控能力,对细节的处理要想透理清,学生可能对活动的目的暂时不太了解,而教师一定要对活动期望达到的结果心知肚明。
数学课程标准中提出“数学教学是活动的教学”,应“向学生提供充分从事数学活动的机会”,但课标所指的“教学活动”是指观察、实验、操作、归纳、类比、猜想、推想、论证、交流、反思等一系列的数学认知活动。
三、素材亟待挖掘
典型的数学活动主要集中在统计、频率等少数几个章节上,实际上,教学的很多内容稍加改造都可以成为很好的数学课题活动素材,而且在常态的课堂教学中,如果能很好地加以运用,对学生数学素养的提升可以说是润物细无声。
1.从定义中来,欲擒故纵,让定义的讲解不再生硬
以“三角函数”的教学为例,定义处理的一贯做法是教师先介绍sin、cos、tan的意义,并且说明是哪两边的比值,接着学生开始记忆、背诵并且强化训练,学生始终处于被动地位。
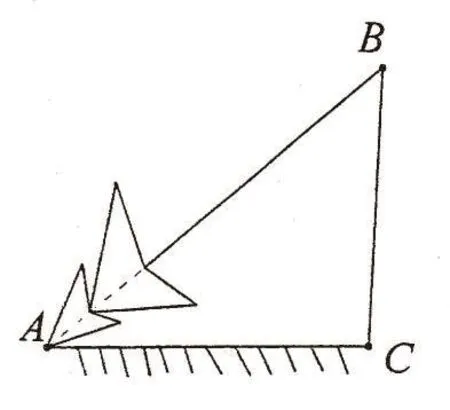
有位教师设置了这样的情境:如图,一棵树在一次台风中被拦腰折断(∠C=90°),设在△ABC中,∠A、∠B、∠C所对的边依次是a、b、c。依据下列数据,你能计算出这棵数的原高吗?
(1)若∠A=30°,还需要测出哪一个数据(只允许一个),就可以计算出原树高?为什么?怎么计算?
(2)如果测得∠A=40°,a=2米,你能求出b、c吗?
教师通过由特殊到一般的类比,激起学生对三角形中的边角关系的重新审视与思考,得出“当直角三角形中一个锐角一定时,那么它的三条边之间存在某种确定的比”的关系,从而使三角函数的定义的引入顺理成章。
2.从定理讲解中来,让定理的证明更加亲切,在不知不觉中得以完成
比如三角形的中位线定理的证明一直是教学中的一个难点,学生很难想到要将中位线延长构成一个平行四边形,有的老师则很好地解决了这个问题。
师:给你一张三角形纸片ABC,你们能将它剪一刀后拼成一个平行四边形吗?(很快,多数学生都完成了任务)
师:你们是沿着哪一条线将三角形剪开的?这条线段的两个端点有什么特点?
由此自然引入中位线的定义,在此基础上,教师又适时引导学生继续观察图形,问你还能得到哪些结论?
经过一番热烈的讨论,学生在互相启发下比较顺利地得到了“三角形的中位线平行于第三边,并且等于第三边的一半”的结论,此时教师要求学生证明这个命题,学生添加辅助线也就水到渠成了。

3.从例题讲解中来,让例题的呈现由平铺直叙到跌宕起伏
有这样一道阅读理解题:在给定的锐角三角形ABC中,求作一个正方形DEFG,使D、E落在BC上, F、G分别落在AC、AB边上,作法如下:
第一步:画一个正方形D1E1F1G1,使D1、E1落在BC上,GI落在AB边上;
第二步:连接BFl并延长,交AC于点F;
第三步:过F点作FE⊥BC,垂足为点E;
第四步:过F点作FG⊥BC,交AB于点G;
第五步:过G点作GD⊥BC,垂足为点D。
四边形DEFG即为所求作的正方形。你能解释其中的原因吗?
笔者选取了两个不同班级进行实验,结果大相径庭。

在甲班按照常规的:出示例题——学生读题——思考——教师提问——讲解的常规顺序进行,最大的感觉就是学生没有多少激情,整个过程显得非常沉闷。
而在乙班采取了下面的方法:
师:现有一张三角形纸片,你能在其中剪出一个正方形吗?如果要剪出一个最大的正方形呢?
一石激起千层浪,学生开始积极行动,有的学生结合自己所掌握的位似的相关知识得出了正确的结论,有的学生百思不得其解,但也兴趣高涨、积极尝试,在此时把题目展示出来,很多学生“如饥似渴”地将题目读完,效果不言而喻。
4.从实际生活中来,用数学的眼光审视身边发生的一切
课堂时间有限,学生的课外生活也是丰富多彩的,作为数学教师,也可以要求学生通过书写数学日记、小论文的方式引导他们关注身边的事。
数学课题活动开展的现状虽然还不尽如人意,但其拓展和提升的空间还很大,只要我们树立起开展数学课题活动的意识,愤而启、悱而发,学生的学习热情需要我们精心设计适当的活动去激发。

