高中物理解题中的常用思维方法总结及分析

吴成奥

摘要：高中物理在笔者看来属于难度相对较大的学科，在这一学科中如果不能运用灵活的思维方式，对于一些复杂的难题就会束手无策。我讲述一下自身在学习过程中总结的一些思维方法并对其进行了分析。希望对其他同学有帮助。

关键词：高中物理 物理解题 思维方法

通过对高中物理的学习，我认为高中物理与其他学科存在着很大区别，高中物理课程的内容大部分都比较抽象，很不容易理解，我们在学习过程中必须找到灵活的适用的方法才能够有效的提高学习物理的效率。

一、正确的思维程序

我在学习和解题的过程中经过反思和总结，认为要想学好高中物理首先要学会正确的思维程序。首先，要学会审题。审清题目是形成正确的解题思路的基础，要仔细阅读题目，在理解题意的基础上找到已知量和未知量是哪些，理解题目中的文字内容，将文字内容转化成为数学公式等，这就为解题确定了初步的思维方向。其次，要对题目进行有效分析。分析题目是整个解题过程之中最重要的一个环节，一道难题能否被解决，关键是看在分析过程中有没有找到正确的解题方向。在分析过程中，要考虑未知量要怎样通过已知量来求出，确定合理的解题思路。在分析过后就是解题的环节，按照之前确定的解题思路进行解题，看看根据目前的解题思路能不能求出对应的结果，如果在解题中遇到困难无法解决，那么就要考虑是否要重新审题和制定解题思路了。在解题完成后还要对所得结果进行检验，同时进行反思和总结，看看自己在解题过程中有哪些步骤想错了，哪些步骤采用了便捷的方法，思考这些方法能不能用在同类型题目的解答上。同时，对于做错的题目自己要准备错题本，在以后做题的过程中要时常查看错题本，以免以后再犯这样的错误。

二、解题中常用的思维方法

（一）等效代替法

我们在日常的解题过程中往往会遇到一些解题步骤极其繁琐的题目，在解这些题目的时候使用一般的解题方法很难得出结果。例如在一些复杂的电路问题中就可以使用等效代替法来解决具体的问题。等效代替法就是使用一些相对来说更简单但是对于解题效果没有影响的物理过程来代替那些繁杂的过程，让复杂的问题变得容易理解。

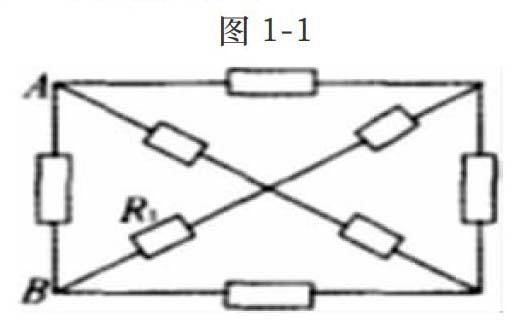
例题：图1-1中有多个不同的电阻，现已知R1=12Ω，其他的电阻值未知，A、B之间的总电阻为4Ω，现将R1电阻值改为6Ω，求A、B之间的总电阻。

这道例题中，给出的已知条件较少，未知量较多。在解答这种类型题目的时候，可以运用等效法，把其他七个未知的电阻用一个电阻R来进行等效代替，在进行替换之后，A、B之间的总电阻就转化成了R1与R两个电阻并联的关系，此时就容易得出A、B之间的总电阻为3Ω。

（二）整体和隔离的方法

整体和隔离的方法也是在解答物理问题时常用的一种方法。整体思想就是在一道题目中将各个有联系的部分看作一个整体来处理，隔离思维则是将物理过程进行细化的层次分析，采用的是分层次分步骤的处理方法，在日常解题过程中很多题目都能用到这种方法。首先通过整体思维找到题目中的隐藏条件和等量关系式，然后将找到的条件进行隔离分析，最终得出结果，这是运用整体和隔离方法的基本解题思路[1]。

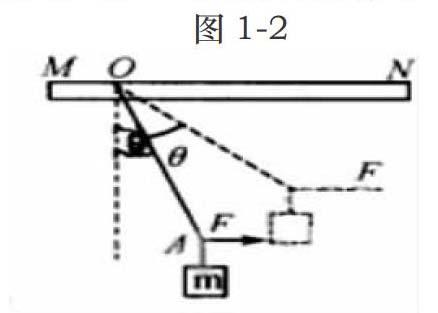
例题：如图1-2，质量为m的物体的一段绑在线绳OA的一边，线绳OA的另一边绑在杆NH的圆环上，水平作用力F拉OA的某一点，让m上升至图中的虚线位置，圆环保持不动。问在这一过程中，拉力F、圆环和水平杆之间的静摩擦力f及圆环与杆之间的压力N的关系是怎样的？

解这道例题时，先从整体上考虑，m在受到力N影响的同时也受到重力影响，重力保持不变，所以N也没有发生变化。在物体静止时，F与f力的大小相同，方向相反。在考虑拉力F的变动时，就要采用隔离的方法将m隔离出去，由图可知，线绳受到张力的竖直分力就是m所受的重力，水平分力就是F，角Θ在这一过程中会扩大，因此F增大，f也变大。

（三）归类转化的方法

对于一些物理问题来说，要想解决问题首先要构建出物理模型，对所得的物理模型进行分类归纳，最后转化成自己学过的知识，解决问题。

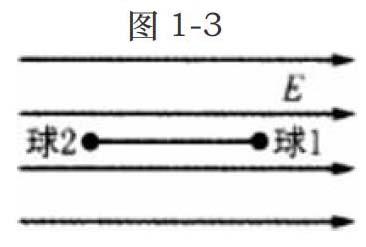
例题：两个质量相同的小球被一条线绳连接在一起，将两个小球放在场强为E的匀强电场中，两个小球都带正电，电量用Q1及Q2表示，Q1大于Q2，如图1-3使线绳与电场方向平行，若将小球由静止状态变为动态，线绳的张力表示为T，计算两个小球与重力之间的库仑力。

从表面上看这是一道电学有关的问题，但根据归纳转化已知条件的过程中了解到两个小球重力相同，并且受到的外力也相同，这样这道题就变成了一道与加速度相关的力学问题，这样的问题根据牛顿第二定律及进行受力分析就能得出答案[2]。

（四）图像法

图像法是指通过图像的方式将复杂的物理关系进行呈现。在解题的过程中有时会遇到无法理解已知量之间关系的问题，这种情况下通过图像法就能够很好的解决问题，图像能够更直接清晰的反映出物理题目中各部分之间的关系。

例题：如图1-4所示，在一种装置上悬挂质量相同的两个小球，小球a在b的上面，将30度的恒力小球施加给小球b，使其保持平衡，达到平衡的效果可以用下面哪个图表示。

首先通过图像做受力分析时，可以将a、b和连线联系在一起，整个悬挂装置受到4个力的作用，并且还有重力的作用，a、b两球上有Fa和Fb两个作用力，线绳产生拉力，在力的相互作用之下达到平衡。从合力为零的角度考虑，Fa和Fb大小相同，方向相反，重力通过m（a+b）g表示，所以图中A是正确的选项。

（五）正向与逆向思维的灵活运用

正向思维就是按照事件发生的先后顺序来解决问题。在物体的运动问题上，就要按照物体的运动由开始运动到结束运动的思维来进行思考。而逆向思维则是从相反的方向来思考问题，像类似于物体运动的问题，运用逆向思维来进行思考的话就是从运动的结束过程开始，推理到运动的去起始阶段。在日常的解题过程中，正向思维是经常被用到的解題思维，对于逆向思维的使用则相对较少，而针对有些题目来说，如果使用逆向思维来进行思考的话，那么往往会起到事半功倍的效果。

（六）综合法

综合法就是将已知的各个部分进行明确的关系划分，然后再将这些部分整合优化，从而实现综合考虑的思维方式。综合法的特点是能够根据已知量来对各个定量进行优化处理。第一，要明确所研究的问题对象，在必要时可以对研究问题的对象进行转换。第二，要明确具体的受力情况，分清楚物体在受力是是受外力的影响还是受原始力的影响更多。第三，根据分析的情况对力的运动做出处理，这里可以运用多种力的分析法则。在这样的分析的基础上进行解题，从而减少解题中的盲目性。

三、结语

以上是我在日常学习和解题的过程中使用的几种解题思维技巧，利用这些思维模式促使笔者在物理学习中有了明显的进步。在解决具体的高中物理问题时，运用正确的、灵活的解题思维方法，往往能够给物理的学习带来事半功倍的效果。

参考文献：

[1]王永刚.掌握正确思维方法探究物理解题途径[J].科教文汇（下旬刊） ，2013，（01）：168 - 169.

[2]赵松年.对高中物理解题思维方法的探究与运用[J].教育教学论坛，2013，（37）：91-92.

（作者单位：枣庄市实验高中）