基于NSCT变换的红外图像增强新算法

严红丽 石永华 孙凯传

(1. 滁州学院电子与电气工程学院， 安徽 滁州 239000； 2. 滁州学院计算机与信息工程学院， 安徽 滁州 239000)

基于NSCT变换的红外图像增强新算法

严红丽1石永华1孙凯传2

(1. 滁州学院电子与电气工程学院， 安徽 滁州 239000； 2. 滁州学院计算机与信息工程学院， 安徽 滁州 239000)

针对夜间红外图像噪声大、对比度低的问题，探讨一种基于正态分布特性和NSCT变换相结合的夜间红外图像增强算法。充分利用了高频子带的系数标准差、系数均值和每个子带系数最大值的构造自适应阈值，保护图像的边缘细节，抑制图像噪声；提出一种新的弱边缘系数增益函数，有效地提升了图像的弱边缘信息。低频系数采用了基于正态分布特性的对比度拉伸增强算法。

红外图像增强； 正态分布； 图像边缘； 自适应阈值

红外成像设备在军事和民用领域应用广泛，但是红外成像设备获取的夜间红外图像受环境影响，存在噪声大、对比度低等缺陷[1]。对红外图像需作进一步的清晰化处理，即红外图像增强。传统的红外图像增强主要采用空域增强法和频域增强法[2]。空域增强法，可直接对图像的灰度值进行处理，通过改变图像像素的分布特性以提升图像对比度，如线性灰度变换、直方图均衡化等。频域增强法，可将图像由空域转换到频域中队频谱并进行相应操作，如频域高通滤波、频域低通滤波等，以达到图像增强的效果。 传统方法在增强图像的同时，图像的噪声同时也被放大，增强效果仍需提高[3]。为此，国内外学者针对红外图像增强作了大量研究[4-6]。

本次研究中，讨论一种新的NSCT变换红外图像增强算法，通过NSCT分解得到高频子带和低频子带系数并进行相应处理，经反变换得到增强后的图像。

1 NSCT变换

NSCT变换和小波变换相类似，也是一种多尺度分解的图像二维表示方法，具有多分辨率、局部定位、多方向性、近邻界采样和各向异性等性质，可将图像分为高频子带和低频子带。NSCT变换具有很好的平移不变性，相比Contourlet变换具有更好的采集规律性，能更好地提取图像本身的信息[7]。

NSCT变换中的滤波器组主要包括拉普拉斯金子塔滤波器结构(LP)和方向滤波器(DFB)(见图1)[8]。LP滤波器主要负责将图像分为高频子带系数和低频子带系数，将高频子带和低频子带分开处理。DFB滤波器负责子带系数的多方向分解，在实际使用中分解的方向数随着尺度的变化而发生变化。NSCT变换可以很好地应用于图像增强处理。

图1 NSCT变换滤波器组结构和频率分解图

2 基于NSCT红外图像增强算法

2.1 高频子带处理增强

图像经NSCT分解之后，高频方向子带系数中包含了图像大部分的细节边缘信息以及几乎全部的噪声。一般情况下，噪声存在于高频子带中绝对值较小的系数之中，对这部分系数需要采取措施加以抑制；而细节边缘信息存在于高频子带中绝对值较大的系数中，这部分系数需要保留或增强。选取一个合适的阈值，将大于阈值的高频子带判别为边缘信息分量，而小于阈值的分量判别为噪声分量。因此，阈值选取合适与否十分关键，直接影响后续的图像处理的结果。文献[9]中对大于阈值的高频子带乘上一个正数进行放大处理。但是由于信号中存在能量较高的区域，若简单地对信号能量较高的部分进行放大，可能会导致边缘过增强，使增强后的图像出现边缘震荡现象。

在此，设定一个阈值，高频子带上大于这个阈值的部分为信号部分。将这部分信号划分为强边缘信号和弱边缘信号，强边缘信号由于边缘信息足够应予以保留，弱边缘信息强度不足则应进行增强处理。高频子带中小于这个阈值的部分是噪声，应予以去除。其算法如下：

(1)

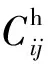
为了使弱边缘信号得到增强，在此应用一种改进的双曲正切函数对弱边缘系数进行增强处理，可避免普通增益函数放大噪声的问题。其算法如下：

(2)

式中，sgn(x)表示符号函数。通过加入符号函数可以保持高频子带系数的符号对应弱边缘的相位不变，增益调节系数的加入使得弱边缘区域得到有效的增强。

2.2 阈值的构造

文献[10]中认为每个子带的阈值为不同值。若对不同尺度、不同方向上的变换系数取同样大小的阈值，并不能很好地估计每个子带的噪声和边缘区域。高频子带系数自适应确定阈值，即在不同尺度和不同方向上自适应地选取不同的阈值。设定阈值和变换系数的标准差成正比[10]：

(3)

然而，若只根据标准取值来构造阈值，并不能有效地估计信号的强度大小。这是因为，某些边缘信号变化不是很大，其标准差取值过小，有可能导致噪声被放大和保留。在此，综合考虑每个高频子带的系数标准差、系数均值和每个子带系数的最大值，得到以下阈值估计式：

(4)

2.3 低频系数增强

经NSCT变换所得到的低频系数，包含了大量图像的基本信息。其图像是除了边缘和轮廓信息之外的图像缩略图，基本不受噪声影响，因此，对低频系数进行增强处理可以提高图像的对比度信息。于是，原始图像对比度受到影响最大。为了有效提高原始图像的对比度，需要对低通子带系数进行拉升，以扩大图像的整体对比度。分析NSCT分解后的低频分量，发现其低频分量的直方图分布近似于正态分布。在此，利用直方图正态分布的特性对低频系数的对比度进行增强处理。对低频分量的截取拉伸算法如下：

(5)

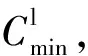
(6)

式中：μ为低频系数的均值；δ为低频系数的标准差；λ为常数，表示在均值附近截取的倍数。从以上分析可以看出，λ取3比较合适。

2.4 算法步骤

(1) 对夜间红外图像进行NSCT分解，将图像分解为高频分量和低频分量。

(2) 利用式(3)求得高频分量分割的阈值，并利用式(1)对弱边缘进行增强处理，对噪声分量予以去除，达到降低图像噪声和提升边缘的目的。

(3) 对低频分量利用直方图截取拉伸进行灰度增强处理，即使用式(4)对低频系数进行处理，提高图像的对比度信息。

(4) 对增强后的高频系数和低频系数进行NSCT反变换，得到增强后的图像。

3 实验结果分析

为检验本算法的应用效果，采集2组夜间红外图像进行对比。NSCT的分解层数是3层，滤波器组选择“9-7”滤波器和“dmaxflat7”滤波器组。对2组图像进行图像增强实验，并选取直方图均衡化与文献[4]的增强图像进行对比。

3.1 第一组红外灰度图像增强实验

对比第一组图像采用几种不同算法的增强实验效果(见图2)，并绘制其对应的直方图(见图3)。

图2 第一组红外图像增强效果对比

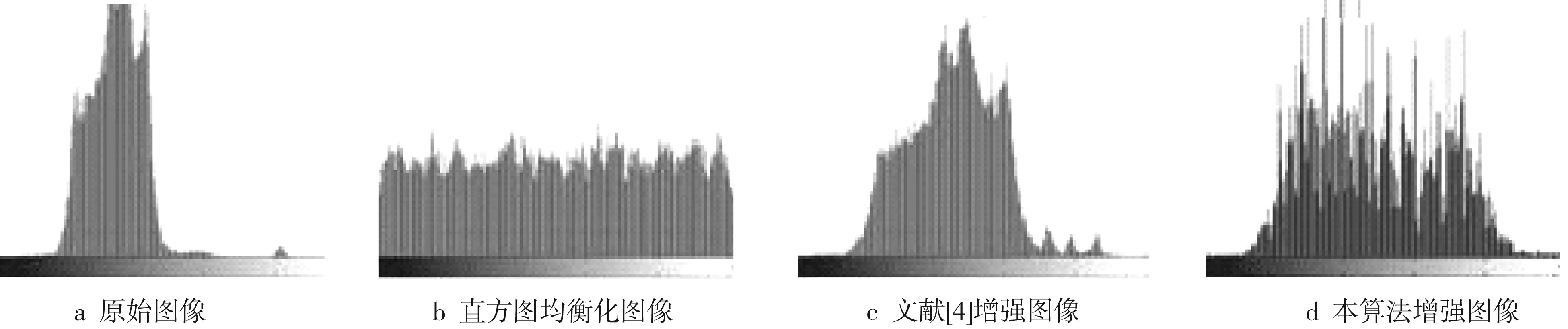
图3 第一组图像效果直方图对比

原始夜间红外图像的质量较差，图像非常模糊，图像的对比度和清晰度较低。从其对应的直方图来看，图像的灰度级集中于低灰度级区域，分布不均，需要采取一定的措施提高图像的质量。采用直方图均衡化方法增强后的图像亮度得到提升，但其对应直方图的图像出现了过增强现象。文献[4]增强图像的总体亮度得到提高，但图像边缘信息未能得到很好的突出，图像仍显模糊。

本算法增强后的图像整体对比度得到大幅提升，图像边缘纹理得到了很好的突出。从直方图分布上看，本算法增强后图像的像素点在整个灰度范围内都得到了有效分布，图像边缘纹理特征也更加凸显，如人体周围的边缘更为清晰。

3.2 第二组红外灰度图像增强实验

对比第二组图像采用几种不同算法的增强实验效果(见图4)，并绘制其对应的直方图(见图5)。

图4 第二组红外图像增强效果对比

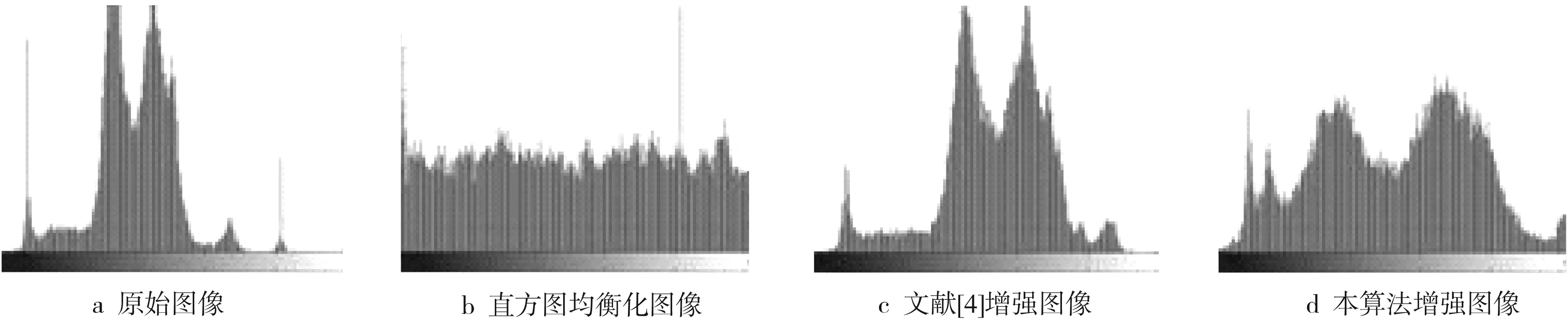
图5 第二组图像效果直方图对比

原始图像中包含较多噪声干扰，图像整体偏暗，且对比度低，图像的边缘和纹理比较模糊。直方图均衡化处理后的图像对比度大大提高，但是局部区域出现过增强现象，有些噪声分量也被增强。此外，增强后的图像在左上角区域出现了噪点，同时直方图均衡化的增强效果无法实现调控；文献[4]增强后的图像亮度和对比度有一定提升，纹理边缘信息也得到突出，但是效果并不显著。

本算法增强后的图像不仅亮度和对比度高，而且有效突出了边缘和轮廓信息，也未出现过增强现象，有效抑制了图像的噪声，具有良好的视觉效果。其直方图显示，增强后的图像灰度级分布相对更加合理。直方图均衡化增强后的局部区域出现过增强现象，且局部噪声也被放大。本算法增强后的图像对比度更高，且未出现过增强现象。

3.3 信息熵指标评价

通过视觉观察能在一定程度上评价图像的质量好坏，但是却不能定量评价图像的质量。为定量的比较几种算法的效果，在此选用信息熵指标评价图像的质量。信息熵能衡量图像的信息量大小，信息熵越大表示图像所含有用信息越多，图像质量越好。

表1 图2中各图像信息熵值

表2 图4中各图像信息熵值

数据显示，本算法增强后的图像信息熵值最高；直方图均衡化和文献[4]中的方法提升了信息熵值，但是其值仍小于本算法增强后的图像信息熵值。本算法有效恢复了红外图像的信息，和主观评价基本一致。综上所述，无论从主观评价还是客观评价方面来看，本算法均优于其他2种算法。

4 结 语

在研究NSCT图像增强算法的基础上，提出了一种新的NSCT变换夜间红外图像增强算法，对NSCT分解之后的高频和低频分量分别进行增强处理。通过高频系数增强处理提高了图像的边缘和轮廓信息，降低了图像的噪声；通过低频分量对图像灰度值的拉伸处理，提升了图像的对比度。后续研究中还需进一步观察红外图像的成像机理，以实现红外图像的自适应增强处理。

[1] 吴强, 王新赛, 贺明, 等. 一种结合小波分析与直方图的红外图像增强方法 [J]. 应用光学, 2011, 32(3): 464-467.

[2] KIM S, KANG W, LEE E, PAIK J. Wavelet-domain color image enhancement using filtered directional bases and frequency-adaptive shrinkage [J]. IEEE Transactions on Consumer Electronics, 2010, 56(2): 1063-1070.

[3] KOBER V. Robust and efficient algorithm of image enhancement [J]. IEEE Transactions on Consumer Electronics, 2005, 52(2): 655-659.

[4] 石丹, 李庆武, 倪雪, 等. 基于 Contourlet 变换的红外图像非线性增强算法[J]. 光学学报, 2009, 29(2): 342-346.

[5] 万智萍. 基于小波 Contourlet 系数相关性的红外图像增强算法[J]. 图学学报, 2014, 35(1): 93-99.

[6] 龚昌来, 罗聪, 杨冬涛, 等. 一种基于平稳小波域的红外图像增强方法[J]. 激光与红外, 2013, 43(6): 703-707.

[7] 吴一全，史俊鹏. 基于多尺度 Retinex的非下采样Contourlet域图像增强[J]. 光学学报,2015,35(3):87-96.

[8] KHAN M A U, KHAN M K, KHAN M A. Coronary angiogram image enhancement using decimation-free directional filter banks[G]∥ Proc. Int. Conf. Acoutics, Speech and Signal Proc.(ICASSP), Montreal, QC, Canada, 2004: 441-444.

[9] 杜超本, 贾振红, 覃锡忠, 等. 基于 NSCT 的遥感图像模糊增强算法[J]. 计算机工程, 2012, 38(4): 188-190.

[10] 梁栋, 殷兵, 于梅, 等. 基于非抽样 Contourlet 变换的自适应阈值图像增强算法[J]. 电子学报, 2008, 36(3): 527-530.

[11] 刘茜, 卢心红, 李象霖. 基于多尺度 Retinex 的自适应图像增强方法[J]. 计算机应用, 2008, 29(8): 2077-2079.

[12] 胡韦伟, 汪荣贵, 方帅, 等. 基于双边滤波的 Retinex 图像增强算法[J]. 工程图学学报, 2010 (2): 104-109.

InfraredImageEnhancementAlgorithmBasedontheNSCTTransform

YANHongli1SHIYonghua1SUNKaichuan2

(1.School of Electronic and Electrical Engineering, Chuzhou University, Chuzhou Anhui 239000, China; 2.School of Computer and Information Engineering, Chuzhou University, Chuzhou Anhui 239000, China)

Because of the low contrast and loud noise of night infrared image, the infrared image enhancement method is presented in this paper, which is based on normal distribution characteristics and NSCT transform. By making full use of the high frequency sub-band coefficient of standard deviation, coefficient of mean and each sub-band coefficient maximum value for the construction of adaptive threshold, the image edge details are protected to better suppress the image noise. It also puts forward a new weak edge gain coefficient function, so weak edge information of the image can be effectively enhanced. The low frequency coefficient is based on the normal distribution characteristics and the contrast is enhanced.

infrared image enhancement; normal distribution; edge of image; adaptive threshold

2017-09-06

安徽省高校优秀拔尖人才培育资助项目 —— 高校优秀中青年骨干人才国内外访学研修重点项目(GXFXZD2016252)

严红丽(1981 — )，女，硕士，讲师，研究方向为信号处理和通信技术。

TP391

A

1673-1980(2017)06-0120-05