基于积累数学活动经验的初中数学教学的研究

王亚平

[摘  要] 基于积累数学活动经验的初中数学教学应该是将培养学生的“双基”增加到培养“四基”，让学生从动手操作过程中的观察思考、对已学概念和定理再思考、对解题过程进行联想等方面积累数学活动经验，以获取解决新问题的思路.

[关键词] 积累;数学活动经验;初中数学;教学研究

如何安排教学才能积累数学活动经验呢？积累了数学活动经验之后，学生在能力和素养方面又有哪些提高呢？在教学实践中我们有这样的体会：学生的数学活动经验是在自己不断地经历、体验各种数学活动的过程中产生的. 更明确地说，要积累数学活动经验，首先应立足于“做”，然后在“做”的过程中思考、总结、积淀. “做”的主体是学生，不过应由教师事先安排;而思考、总结应在“做”的基础上完成，在“做”的过程中完成，且由师生共同完成. 因为有些总结、归纳，单独依靠学生还达不到应有的高度，需要教师的引导.

借助动手操作过程中的观察与思考

新课程理论明确提出，在数学学科里，动手操作也是学习数学的一个重要方法，它是对传统的计算、证明等数学学习方法的有效补充. 另外，还有归纳、猜想等学习方法.

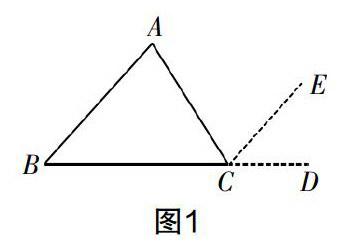
学习“三角形内角和定理及其推论”时，教师对这节课的安排先是再次经历小学已学的折叠、剪拼三角形内角，观察拼图的痕迹，积累“在一个顶点处拼接出一个平角”这一数学活动经验，从而找到添加辅助线的方法. 教材安排的添加辅助线的方法是“（如图1）延长BC到點D，过点C以CD为一边作∠DCE=∠B”，而不是以前的“延长BC到点D，过点C作CE ∥AB”. 这样安排的原因是，从剪拼或折叠三角形的内角中只能直接获得前者这个数学活动经验，而不可能直接获得后者这一经验. 成功地添加出辅助线后，解决问题就变得非常简单了，具体为：如图1，延长BC到点D，过点C以CD为一边作∠DCE=∠B，于是可得CE∥AB. 从而完成将∠A，∠B，∠ACB成功地移至以C为顶点的平角∠BCD，命题的详细证明略.

这里有三个注意事项：（1）应让学生完整地经历这个数学活动过程. 即先经历撕纸、拼图（动手操作）等数学活动，再观察拼图的痕迹（思考猜想），联想出添加辅助线的方法（总结归纳），完成证明过程（抽象思维）. （2）四个环节轻重应不同. 如动手操作在小学时学生已经做过，这里可以加快操作进度;对于总结归纳环节，学生讨论交流后，教师可以引导和帮助;完成证明过程这个环节学生刚刚接触，应以教师示范为主，同时规范书写过程. （3）这是最重要的一点，我们应把动手操作和作辅助线紧密联系起来. 很多教师的处理方式是在不知不觉中将二者割裂，只是为了操作而操作，不利用动手操作获得的数学活动经验去发现如何添加辅助线，这就没有体现二者的联系. 如果将二者割裂，那无论你安排操作与否，实际上都舍弃了通过动手操作积累数学活动经验这一过程，而将其变成了只为解决问题而教学. 不客气地说，这样的教学实际上仍然只停留在注重“双基”上，只实现了一半的收获.

借助已学的概念、定理再思考

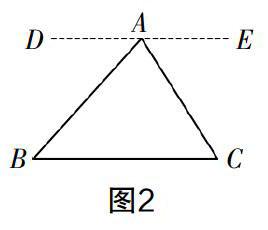
在数学教学中，学习概念、定理是我们的重要任务之一. 结合问题情境，由已学的概念、定理引发再思考，积累新的数学活动经验，也可以获得解决问题的思路. 为了节约篇幅，这里不再重新设置情境，仍以“三角形内角和定理及其推论”为例继续说明教师的再引导：“延长BC到点D，过点C以CD为一边作∠DCE=∠B，可得CE∥AB. 由平行线的性质也可以像刚才的撕纸、拼图一样，完成角的移动，将△ABC的三个内角移至同一个顶点的平角”，也就是说，平行线的性质定理也可以让我们积累这个数学活动经验. 受此经验的启发，笔者引导学生继续探究证明三角形内角和定理的其他方法. 学生自然可以运用这个经验探究出过某一点作一边的平行线，从而得到证明三角形内角和等于180°的很多方法，如图2、图3所示（详解略）.

同理，教师可以再引导：根据我们以往学习定理积累的数学活动经验，对于命题中的180°，除了平角可以得到，我们学过的哪些知识也可以得到呢？启发学生通过“两直线平行，同旁内角互补”及两直角之和等于180°，再探究出新的证明思路. 很多同学根据自己以往学习定理获得的活动经验，想出可以通过“两直线平行，同旁内角互补得到180°”和“两个直角之和等于180°”等. 于是便有了图4、图5等解法（详解略）.

这节课进行到此，应及时总结归纳，积累出系统的数学活动经验. 在一系列探究过程的前提下，教师启发学生思考并总结归纳：这些数学活动经验的本质只有两个方面：（1）在图形中巧妙实现“∠A+∠B+∠C”，也就是将∠A，∠B，∠C移至某一共同顶点处，得到一个平角;（2）除平角外，在图形中再“构造”180°. 两个方面只要实现一个，获取解题思路就成了很自然的事. 因此，证明思路还有很多，根据这节课所得的活动经验，学生课后可以继续探究. 这样的教学过程必然能让孩子们获得系统的数学活动经验，实现数学知识的系统化.

借助解题过程的联想

解题是学生学习数学的重要活动，也是经常进行的数学活动. 解题时，得到解题结果很重要，但解题过程中的思考总结更重要. 数学试题浩如烟海，我们没有必要天天陷在题海中，如果我们能借助解题过程的联想，积累数学活动经验，获取解决新问题的思路，那将受益无穷. 例如，如图6，在△ABC中，M为BC边的中点，AB=5，AC=3，求AM的取值范围.

解决这个问题的关键是添加辅助线，即延长AM至点D，使DM=AM，连接BD，如图7，得到△BMD≌△CMA，从而得到BD=AC. 在△ABD中，利用三角形三边关系求解即可（详解略）.

思考解答此题的数学活动过程，我们可以得到这样一条经验：解决有关三角形中线（或线段中点）的问题时，我们可以通过延长这条中线，构造出全等三角形甚至平行四边形，再解决问题. 下面我们用这个活动经验来解决一个新问题.

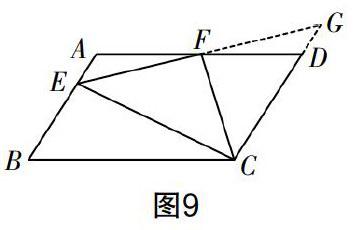
由刚才所得的活动经验，我们可以这样添加辅助线：如图9，延长EF交CD的延长线于点G，从而得到△AEF≌△DGF，接下来问题迎刃而解（其他方法这里不做探究）. 为了表述和记忆的方便，我们可将刚才的数学活动经验称之为“倍中线”.

结语

教学中，类似以上活动的数学活动还有很多，在活动中或活动后进行思考其实更重要，因为思考就能获得数学活动经验，然后利用所获经验解决新问题. 如此循环往复，螺旋上升，不仅可以将学生从题海中解脱出来，还能大幅度地提升他们解决数学问题的能力. 坚持下去，学生的数学素养一定会有较大程度的提高. 这应该就是将培养学生“双基”增加到培养“四基”的重要目的之一.