行和、列和均为素数的九宫格问题探究
龚新平

在平时教学和高考复习中时常会出现一些关于素数的问题,而在各类数学竞赛和自主招生考试中,素数问题更是经常出现的热点题型,有的还颇具难度.以下是对文[1]中提供的2016年全国高中数学联赛江西赛区预赛试卷出现的一个关于行和与列和均为素数的九宫格问题展开的系列探究,最终得出满足条件的所有填法总数,在此以期和大家一起分享.
问题 将前九个正整数1,2,3,4,5,6,7,8,9分别填写于一张3×3方格表的九个格子中,使得每行三数的和与每列三数的和均为素数,请将你的填法填入图1的方格中.
1 探究每行每列三数奇偶性
由于每行三数和为大于2的素数,所以三数和必为奇数素数,从而每行要么三数均为奇数,要么一个奇数两个偶数,同理每列也是三数均为奇数,或者一个奇数两个偶数.由于共四个偶数五个奇数,所以必有某一行且同时有某一列的数全都是奇数.
2 探究最大数的奇偶性组合
考虑与最大数9同行或同列另外两个数的可能性组合,由三数和必为奇数,故这两个数的奇偶性一定相同:若两数均为奇数,则只有(9+1+3),(9+1+7),(9+3+5),(9+3+7)四种情形对应三数和为素数;若两数均为偶数,则只有(9+2+6),(9+2+8),(9+4+6),(9+6+8)四种情形对应三数和为素数.
3 探究互换行(列)及转置情形
由于对符合条件的某种填法,任意互换两行或者任意互换两列,所得九宫格中每行与每列数的和仍为素数,也满足条件;另外,对符合条件的某种填法,同时将第i(i=1,2,3)行转置为第i列,所得九宫格中每行与每列数的和仍为素数,同样满足条件.故我们只需考虑第一行第一列为9且第一行全是奇数的情形,并且考虑第一行或第一次考虑某一列时也先不分前后顺序或上下顺序,然后将得到的每种填法对应的矩阵任意互换两行或任意互换两列,最后再写出前面矩阵对应的转置矩阵,这样得到的所有矩阵就对应着满足条件的所有填法.
4 探究2,8不同行不同列情形
若2与8既不同行也不同列,为了方便不妨记第i行第j列的数为aij,以下分两种情形讨论:
(1)若2、8与9均不同列:如图2,则由步骤三中分析的互换行或互换列及转置对应性,现不妨令a32=6,则a23=4,由此a12≠1,a12≠7,a31≠1,a31≠7,故a13=1或a13=7,从而a12≠5,即必有a12=3,进而必有a31=5,所以a21=1或a21=7,但此时第一列中的三数和为15或21,均不是素数,产生矛盾.
6 探求满足条件所有填法总数
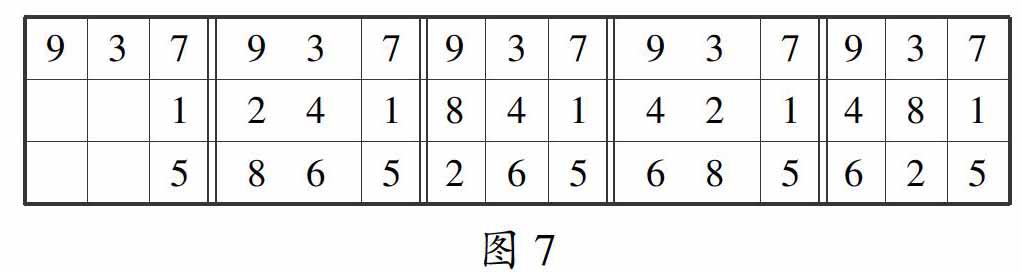
由前面步骤中的分析,可以得到(2×2)×4=16种不同的基本填法;然后将得到的每一种基本填法对应的3×3阶矩阵任意互换两行或互换两列,可以得到A2 3·A2 3=36种不同的矩阵对应的填法,从而总共可得到16×36=576种不同的九宫格填法,然后再加上前面得到的576种填法對应3×3阶矩阵相应的转置矩阵,所有的576×2=1152种矩阵就对应着满足条件的所有填法,故最终可以得到满足条件的所有填法总数为16×36×2=1152种.
参考文献
[1] 《2016年全国高中数学联赛江西赛区预赛》[J].中等数学,2017(5).

