一种基于速度方向修正的旋转稳定弹弹道跟踪制导方法研究

钟扬威,王良明,张立研,叶 昌,史祥鹏

(1.中国航天科工集团 第九总体设计部,湖北 武汉430040;2.南京理工大学 能源与动力工程学院,江苏 南京 210094;3.国营洛阳丹城无线电厂,河南 洛阳 471000)

一种基于速度方向修正的旋转稳定弹弹道跟踪制导方法研究

钟扬威1,王良明2,张立研3,叶 昌1,史祥鹏1

(1.中国航天科工集团 第九总体设计部,湖北 武汉430040;2.南京理工大学 能源与动力工程学院,江苏 南京 210094;3.国营洛阳丹城无线电厂,河南 洛阳 471000)

针对旋转稳定二维弹道修正弹的制导律设计问题,提出了一种基于速度方向修正的弹道跟踪制导方法,推导了固定舵产生阶跃激励时弹丸的攻角及速度运动规律,得到了平均偏角的相位角与固定舵滚转角的关系。通过在标准弹道上生成一个虚拟未来点,得到了速度角的指令。提出了通过修正速度方向与该指令的偏差,实现对标准弹道跟踪的原理。提出了一种当实际弹道偏离标准弹道较远时,通过落点预测实时生成新的标准弹道的方法。仿真结果表明:小射角射击时,可在全弹道采用速度方向修正来跟踪标准弹道;大射角射击时,可在降弧段在线生成标准弹道,再通过速度方向修正来跟踪该标准弹道。

旋转稳定弹;角运动;弹道;制导

在精确打击的战场需求牵引下,精确制导弹药将成为未来战争的主战武器装备。为发展具有精确打击能力的旋转稳定弹,国外首先提出了基于固定舵修正机构的二维弹道修正弹。该弹的弹体高速旋转以保证陀螺稳定,固定舵可绕弹轴低速旋转或固定在某一方位。这种方案对原弹的改动小、成本低,同时便于通用化,是高旋弹制导化的一种发展趋势。

对于尾翼稳定制导弹,弹轴在控制力矩作用的平面内摆动,使得弹轴的摆动方向和控制力矩之间的关系明确,目前主要采用弹道跟踪制导[1]及末段比例导引[2]。而对于旋转稳定二维弹道修正弹,由于弹体高速旋转的陀螺效应,其弹轴摆动为二圆运动,高低和方向攻角形成复杂的外摆线运动。控制力实施后,弹轴将向垂直于控制力矩作用的平面内摆动,产生空间章动和进动,这使控制力矩方向与弹丸受控以后摆动方向之间的关系变得十分复杂。因此,需对在控制力作用下高旋弹丸的弹轴运动、质心运动规律研究透彻后,才能提出合适的制导方法。目前相关学者对该类弹丸的落点预测方法[3-4]、落点运动规律[5-7]及落点预测制导方法[8]进行了研究。

本文针对旋转稳定二维弹道修正弹的运动特点,提出了一种弹道跟踪制导方法。该方法通过对速度方向的修正,实现对标准弹道的跟踪。首先推导并分析了弹丸在固定舵作用下的攻角及速度运动特性。然后给出了制导指令的生成模型,及修正速度方向所需的固定舵滚转角的计算公式。探讨了在实际弹道偏离标准弹道较远时,通过落点预测在线生成标准弹道的方法。最后在2个射角下对制导方法进行了仿真分析。

1 有控时固定舵产生的角运动及对速度方向的影响分析

1.1 有控时固定舵产生的角运动

根据旋转稳定二维弹道修正弹的质心运动方程和绕质心转动方程,可以推导得到弹丸的复攻角运动方程为[9]

(1)

式中:

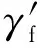
有关符号的表达式为

(2)

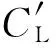
固定舵产生阶跃控制激励时,ωf=0,在零初始条件下,由固定舵产生的角运动方程可写为

Δ″+(H-iP)Δ′-(M+iPT)Δ=Kε(s)

(3)

式中:ε(s)为单位阶跃函数。

γfc为有控时固定舵的滚转角。

阶跃激励是一个突加的常值激励,可以设立新坐标:

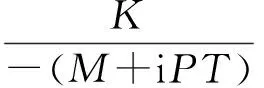
(4)

将式(4)代入到式(3),得:

(5)

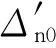
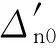
(6)

式中:s为弹道弧长,l1=λ1+iω1,l2=λ2+iω2,λ1和ω1分别为快圆运动的阻尼和频率,λ2和ω2分别为慢圆运动的阻尼和频率。

1.2 有控时固定舵产生的角运动对速度方向的影响分析

固定舵产生控制力后,弹丸的攻角会发生变化,并在攻角面内产生升力。由于攻角面不断绕速度线旋转,升力方向也就不断地改变,于是速度方向也在不断旋转改变。引入复偏角Ψ=Ψ1+iΨ2,则在攻角产生的升力和固定舵产生的控制力作用下,弹丸复偏角的导数为

(7)

将固定舵产生阶跃激励时的攻角(6)代入,得:

(8)

将s=vt代入式(8),并从0到tc积分得:

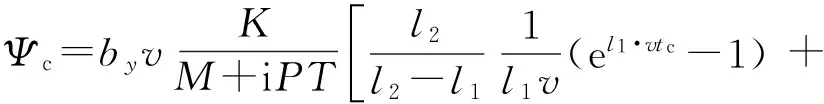
(9)

式中:el1·vtc和el2·vtc为周期衰减项,可忽略,只考虑偏角的平均位置,化简得:

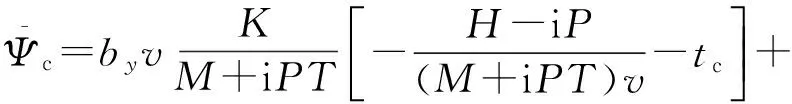
(10)

将K代入式(10),并将vδzeiγfc提出来,得：

(11)

将式(11)写成下面的形式:

(12)

则得到下式:

φψ=γfc+χ

(13)

式(13)说明偏角平均位置的相位角较固定舵滚转角超前了一个前置角χ,χ的物理解释及计算公式参考文献[10]。

2 基于速度方向修正的旋转稳定弹弹道跟踪制导方法

2.1 弹道跟踪制导指令生成

二维弹道修正弹在发射前,火控计算机根据阵地坐标、敌方目标及相关条件,解算出火炮射击高低角和方位角,然后根据解算结果,仿真出一条弹道,从该弹道上取一些特征点的位置坐标存储在弹载计算机上,标准弹道就由这一系列位置坐标连成的线段组成,如图1所示。

在进行标准弹道跟踪制导时,首先把弹丸当前实际位置O投影到标准弹道上,得到投影点OP,然后在点OP后沿着标准弹道附加一定的缓冲距离BL,由此得到的虚拟未来坐标点当作是位置跟踪指令点OT。随着OT在标准弹道上不断地向前移动,弹丸在其引导下逐渐飞向标准弹道,如图2所示。

对于标准弹道上的每一段跟踪弹道,其空间方程是确定的,可表示为

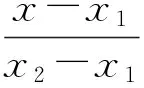
(14)

式中:(x1,y1,z1)、(x2,y2,z2)分别为每段跟踪弹道的起点和终点。设弹丸在任意时刻的坐标为(x,y,z),则弹丸在跟踪弹道上的投影坐标为

(15)

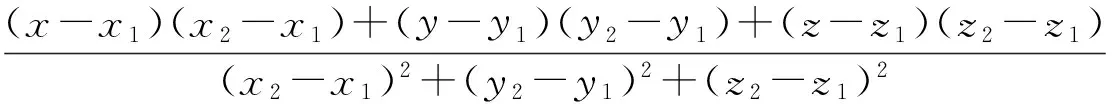
在跟踪线段上取距离弹丸投影点缓冲距离BL的虚拟点作为跟踪点时会有2种情况,需要分别考虑。

第一种情况是缓冲距离不大于投影点到跟踪线段末端的距离,这种情况下,期望的跟踪坐标指令(xc,yc,zc)仍在当前跟踪线段上,其计算公式为

(16)

第二种情况是缓冲距离BL大于投影点到跟踪线段末端的距离DT。这种情况下,跟踪点需延长到下一段跟踪线段上,则:

(17)

由此,可以得到速度高低角和速度方位角的指令为

(18)

2.2 基于速度方向修正的跟踪制导方法

得到速度高低角和速度方位角的期望指令后,本文提出了一种基于速度方向修正的标准弹道跟踪制导方法,其原理是消除弹丸速度矢量v和从弹丸质心到弹道跟踪指令点的矢量vT之间的夹角,如图3所示。

由图3可知,速度高低角和速度方位角的增量Ψ1和Ψ2分别为

(19)

当有风时,需要固定舵修正的速度方位角为

(20)

(21)

(22)

由速度方向变化的相位角,求出所需的固定舵滚转角为

γfc=φψ-χ

(23)

3 一种跟踪弹道的在线生成方法

弹丸飞行过程中,有时可能实际弹道偏离标准弹道较远。固定舵修正能力有限,使得弹丸最后不能准确修正到该标准弹道上。此时,需要设计一条新的标准弹道。本文给出了一种在实际弹道偏离标准弹道较远时,在线生成新的标准弹道的方法。

弹丸飞行过程中,由卫星可实时测得弹丸在地理坐标系中的空间位置及速度。通过坐标转换可得到生成弹道起始点处,弹丸在地面坐标系中的位置坐标为(x0,y0,z0),速度大小、高低角和方位角分别为v0,θa0,ψ20。再根据目标坐标(xm,zm),生成标准弹道的步骤如下。

①积分第一条弹道。

根据(v0,θa0,ψ20,x0,y0,z0),通过修正质点弹道方程积分,得到落点处的坐标(xf1,zf1)。

②积分第二条弹道。

计算速度方向角的修正量为

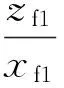
(24)

令θa1=θa0+Δθa(Δθa可以设定一个初始值),ψ21=ψ20-Δψ2,积分第二条弹道,得到落点处的坐标xf2和zf2。

③迭代速度高低角和速度方位角。

计算高变量及速度方向角修正量分别为

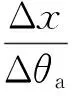
(25)

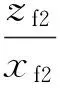
(26)

则速度高低角和速度方位角的迭代公式为

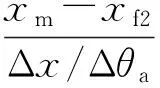
(27)

ψ22=ψ21-Δψ2

(28)

一般按步骤③迭代几次就能满足精度要求:①距离偏差|Δx|

4 算例

以某型旋转稳定二维弹道修正弹为对象进行制导仿真,其中拉偏参数:初速偏差值为5 m/s,起始横向摆动角速度偏差值为3 rad/s,起始纵向摆动角速度偏差值为3 rad/s,射角偏差值为2 mil,射向偏差值为2 mil,阻力系数偏差值为-1%,横风偏差值为5 m/s,纵风偏差值为5 m/s。测量及控制偏差:水平定位偏差值为5 m,垂直定位偏差值为10 m,水平测速偏差值为0.2 m/s,垂直测速偏差值为0.3 m/s,滚转角控制偏差值为2°,目标探测偏差值为5 m。末段高度离地面3 000 m时,直接跟踪目标点的坐标,高度离地面50 m时停止修正,弹丸以惯性飞行。

4.1 35°射角时的仿真分析

35°射角时,从出炮口15 s开始修正,得到的仿真结果如图4～图7所示。图4、图5分别为射程-高度曲线及射程-侧偏曲线。

图6为修正弹道攻角曲线,图7为固定舵滚转角曲线(前15 s时为0表示不进行修正)。

从图4、图5可以看出,35°射角时,拉偏弹道的落点偏差为(507 m,210 m)。15 s开始修正后,修正弹道的落点偏差为(-13 m,3 m)。从图6看出,修正弹道的攻角呈现复杂的外摆线运动。

4.2 51°射角时的仿真分析

51°射角射击时,从出炮口15 s开始修正的仿真结果如图8和图9所示。从图8、图9可以看出,拉偏弹道的落点偏差为(662 m,310 m)。从出炮口15 s开始修正后,固定舵在升弧段能将实际飞行弹道拉回到标准弹道上。但由于此时的弹道高达10 km,固定舵的修正能力不足以让弹丸稳定在标准弹道附近飞行,这使得弹丸重新偏离标准弹道较远,在降弧段也无法修正回来,造成较大的落点偏差。

下面根据本文提出的在线生成标准弹道的方法,在降弧段生成一条新的标准弹道。生成标准弹道经过5次迭代,每1次迭代后的误差如表1,最后生成的标准弹道的落点偏差为(0.4 m,10.9 m)。跟踪该标准弹道的仿真结果如图10～图13所示。

表1 每次迭代后的误差

从图10和图11看出,51°射角时,跟踪降弧段在线生成的标准弹道,弹丸落点相对于实际目标点的偏差为(-12 m,-5 m),可见跟踪在线生成的标准弹道可显著提高落点修正效果。从图13看出,修正时固定舵滚转角变化较缓慢,便于进行滚转角控制。

5 结束语

旋转稳定二维弹道修正弹的强陀螺效应使得攻角、速度的响应不在控制力作用的方向上,因而传统的制导方法很难用在该类弹丸上。为此,本文提出了一种基于速度方向修正的标准弹道跟踪制导方法,主要工作如下:

①推导了固定舵产生阶跃激励时,弹丸的攻角运动及速度运动特性,得出平均偏角的相位角较固定舵滚转角超前了一个前置角。

②提出了一种基于速度方向修正的跟踪制导方法。该方法首先在标准弹道上生成一个虚拟未来点,从而得到速度角的指令。通过修正弹道速度方向与该指令的偏差,实现对标准的跟踪。

③针对实际弹道偏离标准弹道较远的情况,提出了一种经过少数几步迭代在线生成新的标准弹道的方法,仿真结果证明了该方法是有效的。

④分析35°射角时的仿真结果可以看出,小射角时从15 s开始修正能满足落点修正效果要求。

⑤分析51°射角时的仿真结果可以得到,大射角下从15 s开始修正不能满足落点修正效果要求,而跟踪降弧段在线生成的标准弹道可以得到较好的落点修正效果。

[1] 杨荣军,叶瑶,闫德恒,等.滑模控制在制导弹药弹道跟踪中的应用[J].弹道学报,2015,27(4):24-29.

YANG Rong-jun,YE Yao,YAN De-heng,et al.Application of sliding mode control on trajectory following for munitions[J].Journal of Ballistics,2015,27(4):24-29.(in Chinese)

[2] 牟宇,林德福,祁载康,等.激光末制导炮弹比例导引律性能研究[J].红外与激光工程,2009,38(2):250-255.

MOU Yu,LIN De-fu,QI Zai-kang,et al.Performance of proportional navigation law for terminal laser-guided projectile[J].Infrared and Laser Engineering,2009,38(2):250-255.(in Chinese)

[3] 王毅,宋卫东,宋谢恩,等.基于摄动理论的弹道修正榴弹落点偏差预测[J].弹道学报,2015,27(3):18-23.

WANG Yi,SONG Wei-dong,SONG Xie-en,et al.Impact-point prediction of trajectory-correction grenade based on perturbation theory[J].Journal of Ballistics,2015,27(3):18-23.(in Chinese)

[4] 王钰,于纪言,王晓鸣.摄动落点预测法的快速建模与基于精度最优的分段预测控制法[J].兵工学报,2017,38(5):867-876.

WANG Yu,YU Ji-yan,WANG Xiao-ming.Rapid impact-point prediction modeling based on perturbation theory and piecewise prediction control method[J].Acta Armamentarii,2017,38(5):867-876.(in Chinese)

[5] 王毅,宋卫东,宋谢恩,等.固定鸭舵式二维弹道修正榴弹偏流特性分析[J].系统工程与电子技术,2016,38(6):1 367-1 373.

WANG Yi,SONG Wei-dong,SONG Xie-en,et al.Ballistics drift analysis of 2D trajectory correction projectiles with fixed-canards[J].Systems Engineering and Electronics,2016,38(6):1 367-1 373.(in Chinese)

[6] 王钰,王晓鸣,程杰,等.基于等效力方法的双旋弹侧向控制力落点响应分析[J].兵工学报,2017,37(8):1 379-1 387.

WANG Yu,WANG Xiao-ming,CHENG Jie,et al.Analysis on impact point response of a dual-spin projectile with lateral force based on equivalent force method[J].Acta Armamentarii,2017,37(8):1 379-1 387.(in Chinese)

[7] 黄伟,高敏,王毅,等.固定鸭舵控制误差对修正弹落点散布的影响[J].探测与控制学报,2017,39(3):70-74.

HUANG Wei,GAO Min,WANG Yi,et al.Influence of fixed canard control error on dispersion of trajectory correction projectile[J].Journal of Detection & Control,2017,39(3):70-74.(in Chinese)

[8] GAGNON E,VACHON A.Efficiency analysis of canards based course correction fuze for a 155mm spin-stabilized projectile[J].Journal of Aerospace Engineering,2016,29(6):04016055.

[9] 钟扬威.旋转稳定二维弹道修正弹弹道特性分析与制导方法研究[D].南京:南京理工大学,2017.

ZHONG Yang-wei.Study on trajectory characteristics and guidance methods for spin stabilized two-dimensional trajectory correction projectiles[D].Nanjing:Nanjing University of Science and Technology,2017.(in Chinese)

[10] 吴映锋,钟扬威,王良明.旋转稳定二维弹道修正弹在固定舵作用下的角运动特性研究[J].兵工学报,2017,38(7):1 263-1 272.

WU Ying-feng,ZHONG Yang-wei,WANG Liang-ming.Study on angular motion characteristics of spin-stabilized 2D trajectory correction projectile under the effect of fixed canards[J].Acta Armamentarii,2017,38(7):1 263-1 272.(in Chinese)

[11] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:186-188.

HAN Zi-peng.Exterior ballistics of shells and rockets[M].Beijing:Beijing Institute of Technology Press,2008:186-188.(in Chinese)

StudyonTrajectoryTrackingGuidanceMethodforSpinStabilized
ProjectileBasedonVelocityDirectionCorrection

ZHONG Yang-wei1,WANG Liang-ming2,ZHANG Li-yan3,YE Chang1,SHI Xiang-peng1

(1.The 9th Designing,CASIC,Wuhan 430040,China;2.School of Energy and Power Engineering,NUST,Nanjing 210094,China;3.Luoyang Dancheng State-owned Radio Factory,Luoyang 471000,China)

A trajectory tracking guidance method based on velocity direction correction was proposed for the design of guidance law of spin stabilized 2D trajectory correction projectile(TCP).The laws of attack angle motion and velocity motion while the fixed canards generated step excitation were derived,and the relationships between the phase angle of average deflection angle and the roll angle of fixed canards were obtained.By generating a virtual future point on the standard trajectory,the commands of the velocity angles were obtained.The principle was proposed by correcting errors between the velocity direction and the commands,and the tracking of standard trajectory was achieved.A new standard trajectory can be generated in real time through the impact point prediction while the actual trajectory is far away from the standard trajectory.The simulation results show that,when the firing angle is small,the velocity direction correction can be used to track the standard trajectory on the whole trajectory.When the firing angle is large,the standard trajectory can be generated on downward phase,and then the velocity direction correction can be used to track the new standard trajectory.

spin stabilized projectile;angular motion;trajectory;guidance

TJ303.4

A

1004-499X(2017)04-0015-07

2017-09-19

十三五装备预研基金项目(0715A)

钟扬威(1989- ),男,工程师,博士,研究方向为新型弹箭外弹道理论及应用。E-mail:123161506@qq.com。