轻武器榴弹射击密集度试验方法研究

蒲利森,徐酉亮

(中国白城兵器试验中心,吉林 白城 137001)

轻武器榴弹射击密集度试验方法研究

蒲利森,徐酉亮

(中国白城兵器试验中心,吉林 白城 137001)

为研究确定轻武器榴弹射击密集度的试验方法,结合轻武器榴弹鉴定试验时的操作实际,对气象条件、弹丸初速、射角、弹道系数等影响因素进行了分析,找到了影响轻武器榴弹射击密集度散布变化的关键因素。通过运用数理统计理论建立了方差检验模型,对有关产品在不同状态下的密集度散布方差进行了检验分析。检验结果表明,弹温对密集度散布没有影响,而分组试验能够消除偶然因素带来的不利影响。为保证试验条件的一致性,建议密集度试验采用在标准温度下分3组进行的试验方法。

轻武器榴弹;密集度试验;方差检验;标准温度

所谓射击密集度是指弹丸落点对散布中心的偏离程度,它是用散布误差的大小来衡量的,反映了同样的瞄准条件下射击各发弹对散布中心的离散程度[1]。鉴于不同时期发布的弹药试验军用标准规定的密集度方法不尽相同,有的要求采用常温、高温和低温3种温度条件,有的只要求自然温度;有的温度条件下射击3组,有的温度只要求射击1组;发射后经测量弹着点坐标进而计算得到弹丸射击密集度[2-4]。鉴于轻武器榴弹的弹丸轻、初速低,温度和分组情况不同能够对密集度产生多大影响,采用哪一种试验方案更加科学合理,是客观评价弹药密集度的迫切需求。为此,本文结合试验时采用固定枪架夹持弹道发射器单发射击榴弹的实际,利用外弹道理论对弹药散布的影响因素进行分析,借鉴查阅的多种轻武器榴弹密集度试验档案数据,运用数理统计理论对不同温度及分组条件下弹丸散布试验结果进行分析验证,研究了不同温度及分组条件下弹丸散布差异的影响程度及因素,为确定轻武器榴弹密集度试验方法提供了参考[5-7]。

1 试验影响因素分析

根据弹丸散布计算模型可知,弹丸的散布精度主要受试验时的气象条件、弹丸初速、射角、弹道系数等因素变化影响。下面结合轻武器榴弹鉴定试验时的操作实际对影响因素逐一进行分析,从而找出影响轻武器榴弹密集度散布变化的关键因素,为研究建立科学、合理的密集度试验方案提供理论依据。由外弹道理论可得弹丸的距离中间误差计算关系式为[8]

(1)

式中:QC为弹道系数变化1%时的射程修正量,EC为弹道系数相对中间误差,Qv0为初速变化1 m/s时的射程修正量,Ev0为初速相对中间误差,Qθ0为射角变化1′时所引起的射程修正量,Eθ0为射角相对中间误差,Qwx为纵风为1 m/s时的射程修正量,Ewx为纵风相对中间误差。

根据上述外弹道模型可知,影响密集度的因素有EC,Ewx,Eθ0和Ev0。鉴于弹道系数与其本身的形状结构密切相关,其值大小主要由弹丸的截面密度和弹形系数决定,由于弹温变化不会引起弹丸的结构发生显著变化,即由弹温变化造成的弹道系数相对中间误差EC变化很小,可以忽略不计。纵风相对中间误差Ewx主要是由自然条件造成的,不是人为的方法可以任意改变的,因此与弹温没有直接相关性。依据现有的轻武器弹药试验军用标准规定:密集度试验时采用固定发射架夹持弹道发射器单发射击榴弹,可以认为射角在整个试验过程中不变,即Eθ0不变,因此无论弹药温度如何变化,其发射角度不会引起弹丸落点散布的显著变化。可见采用固定架夹持射击并严格控制气象条件的情况下,对密集度的影响主要是由初速相对中间误差Ev0引起的,只要初速误差满足散布的一致性,弹温对密集度就没有显著影响。

2 检验分析模型

零假设H0:σA=σB;备择假设H1:σA≠σB。

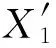
2.1 计算统计量值

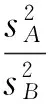
(2)

式中:

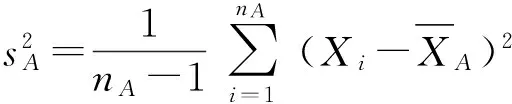
根据显著水平α,以ν1=nB-1,ν2=nA-1为自由度,查F分布分位数表,得到Fα/2(nB-1,nA-1)和Fα/2(nA-1,nB-1)。

从而求得:

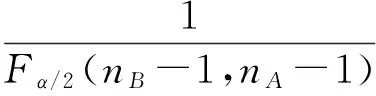
(3)

2.2 判定

若FFα/2(nA-1,nB-1),则拒绝假设H0,即认为σA与σB不等;若F1-α/2(nA-1,nB-1)≤F≤Fα/2(nA-1,nB-1),则不能拒绝H0,即无理由认为σA与σB不等[9]。

3 统计检验

3.1 温度变化对初速散布的影响分析

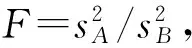
从表1统计结果可以看出,除了杀伤弹和杀伤燃烧弹的高温与低温的方差比值超出α=0.05时的统计量F值范围外,其余统计结果均满足,因此可以认为当α=0.05时弹温对初速散布基本没有影响。

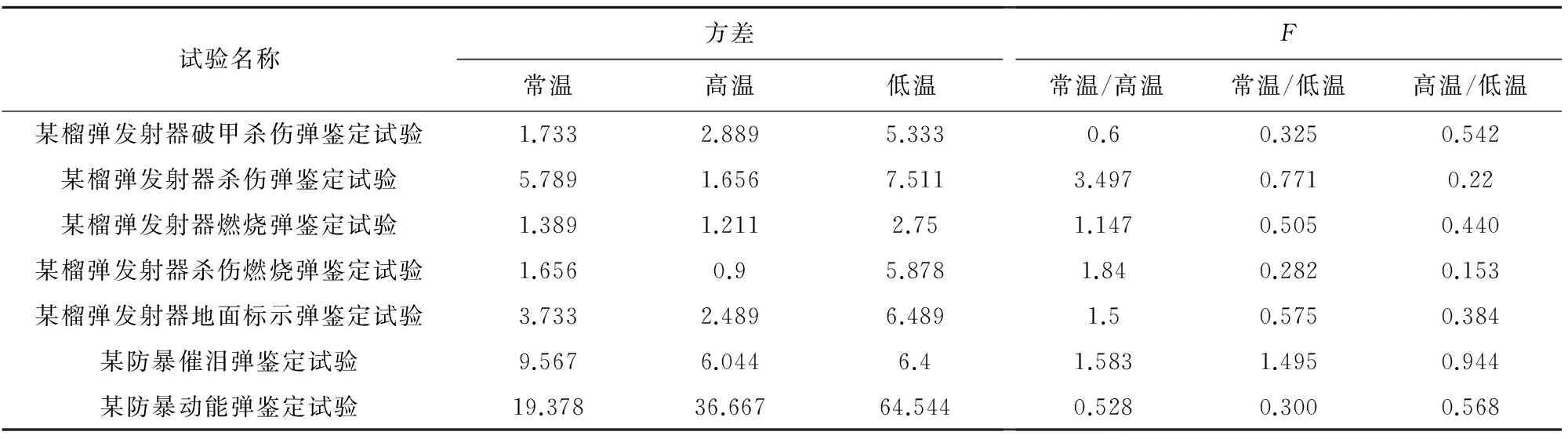
表1 弹温对初速散布影响方差检验表

3.2 温度及分组对密集度散布的影响分析

为了验证温度及分组因素对密集度的影响,先不考虑温度和分组因素单独对密集度的影响,而是分析多种因素共同作用下对密集度的影响,看统计量F值对零假设的符合程度,下面以某杀伤弹鉴定试验结果为例进行说明。图1为某杀伤弹所有条件下密集度方差检验图,图中m为组序。

从图1可以看出,所有条件下的统计量F曲线只有密集度试验弹丸的方向落点散布方差(z方向)少部分超出了临界区间,而距离落点散布方差(x方向)全部都在临界区间内,表明它们的统计量F基本满足零假设H0,故没有理由认为所有条件下弹丸的密集度不一致,少数部分不满足可能是由偶然因素造成的,本文下面分析温度、分组因素分别对密集度的影响。

3.3 温度变化对密集度散布的影响分析

为了验证弹温变化对密集度造成的影响,利用上述检验模型分别检验了不同温度之间和同种温度不同组之间的方差一致性,看统计量F值是否满足零假设H0,如果同种温度不同组之间仍然存在超出临界区间的情况,说明弹温不是引起密集度变化的唯一因素,从而推断弹温对密集度的影响程度。图2和图3分别为某杀伤弹不同温度之间和同温不同组条件下密集度方差检验图。

从图2和图3可以看出,进行不同温度之间方差检验时,方向和距离比值均有部分超出临界区间,而同温不同组之间仍然有超出临界区间的现象,说明单一温度条件下各组之间的方差散布也存在差异,这种差异除去弹药自身的波动性外极有可能是由偶然因素造成的,为此针对不同温度3组平均后再进行比对,分析采用多组的试验方法能否消除偶然因素带来的影响。

3.4 分组因素对密集度散布的影响分析

为全面检验分组因素对密集度散布变化的影响,采取先进行同种温度条件下3组弹丸落点散布方差平均计算，再运用上述检验模型对弹丸落点散布平均后的方差进行不同温度之间的一致性检验分析,看同种温度条件下多组试验方案能否引起散布方差一致性的变化,图4为某杀伤弹同温条件下方差平均后的检验图。

从图4可以看出,无论是方向还是距离均在临界范围内, 说明通过增加试验子样并采取分组的方法能够消除偶然因素造成的误差影响。由此可见,采用3种温度进行试验的方法是没有必要的,也是不可取的。

3.5 统计结果及分析

为了确保密集度试验方法科学且合理可行,通过对建场以来的所有轻武器榴弹密集度试验数据进行方差检验分析,根据榴弹试验标准通用规定,取置信水平α=0.05。由于篇幅的关系,本文只给出了部分弹药是否满足零假设的情况,没有给出具体的数值,统计结果如表2所示。表2中“合”代表满足假设H0,“不合”代表满足假设H1。

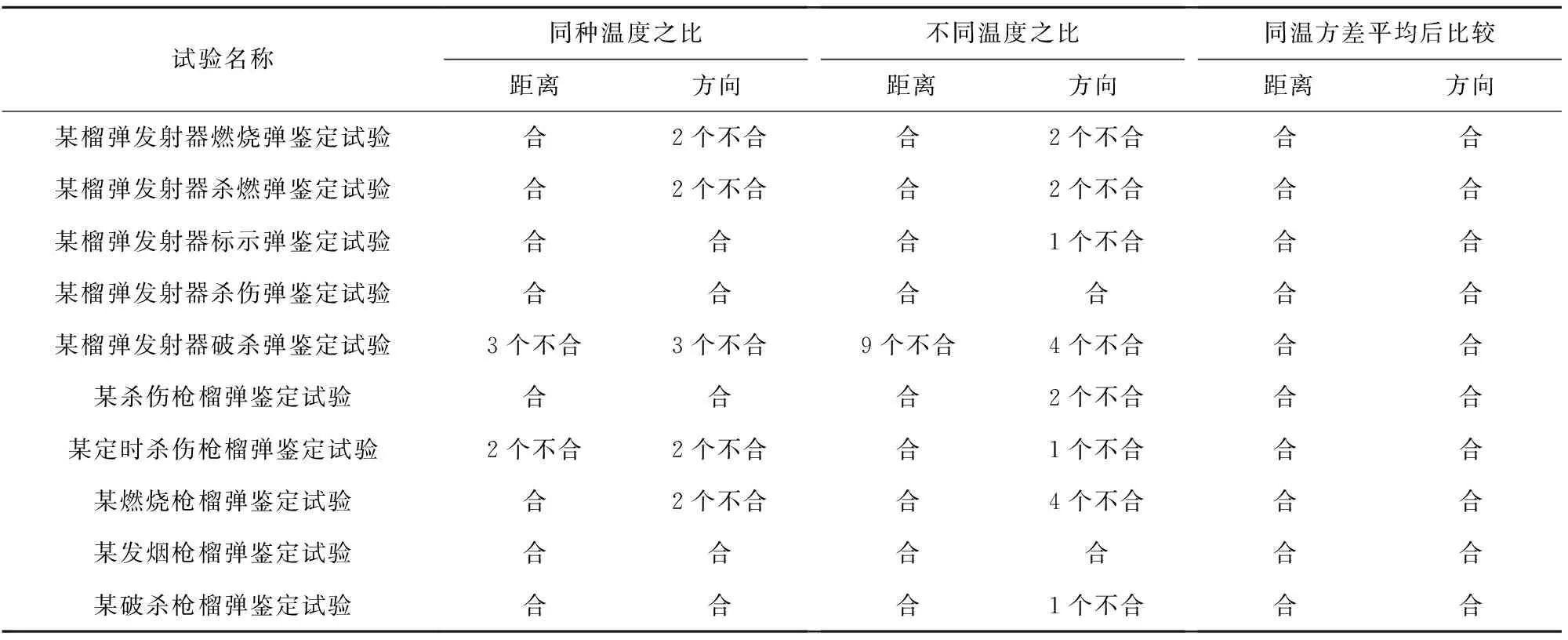
表2 当α=0.05时弹温对密集度的影响统计结果表

利用前面建立的数学模型并对近年来多个产品的初速和密集度进行统计分析,根据统计结果,当置信水平α=0.05时,可以得出以下基本论断:

①初速的常温/高温以及常温/低温方差相比的F值100%满足零假设,高温/低温的F值有77.78%满足零假设。说明它们的散布基本相同,因此当α=0.05时弹温对初速散布影响较小。

②通过对产品所有条件下的方差进行比较,发现它们的距离方差比值有92.25%满足零假设,方向方差比值有82.84%满足零假设,说明它们的方差是基本一致的,少数部分没有满足零假设可能是由于试验过程中的偶然因素造成的,并不是因为弹温变化造成的弹丸散布的变化。

③通过对产品进行同温不同组之间方差的比较,发现在同温条件下不同组之间的距离方差比值有92.98%满足零假设,方向上的方差比值有79.53%满足零假设,这个比例与3种温度条件下所有方差比值满足零假设的比例基本一致,进一步说明弹温对密集度影响不是主要因素。

④通过对产品进行不同温度条件下的方差比较,发现在不同温度条件下的距离方差比值上有92.01%满足零假设,方向上的方差比值有84.74%满足零假设,这个比例与结论②所有条件下的方差比值满足零假设以及同温条件下不同组之间的方差比值满足零假设的比例基本一致,更进一步证实弹温对密集度是没有影响的。

⑤在对同种温度条件下的多组射弹落点散布方差进行平均处理后,再对不同温度之间的落点方差进行一致性检验。发现在同温条件下多组方差平均后3种温度之间进行方差比较,无论是距离上还是方向上基本不会出现方差比值不满足零假设的情况,说明通过多组试验可以消除偶然因素对密集度的影响。 由此可见,采用3种温度进行试验的方法是没有必要,也是不可取的;而采用多组试验来消除偶然因素影响反而十分必要。

4 结束语

根据前面的理论分析以及统计检验结果,建议在今后的轻武器榴弹密集度试验中采用单一温度条件下射击多组的方法进行试验。同时为了更好地降低偶发因素带来的散布影响,保证射击条件的一致性,应对弹药温度范围加以适当限定,按照轻武器射表试验关于弹药温度的通用要求,可规定弹药温度为标准温度,以此提高弹药射击密集度试验结果的准确性。据此可规定轻武器榴弹密集度试验方法为:地面风速小于5 m/s,用固定架夹持枪械向规定距离上的靶标射击标准温度榴弹3组,每组7～10发,射后逐发测试弹丸散布坐标,计算每组弹的散布中间误差及组平均值。

[1] 徐培德,谭东风.武器系统分析[M].北京:国防科技大学出版社,2001:101-108.

XU Pei-de,TAN Dong-feng.Weapon system analysis[M].Beijing:National University of Defense Technology Press,2001:101-108.(in Chinese)

[2] 杨国富.GJB349.18-89 常规兵器定型试验方法破甲、杀伤、破甲杀伤两用枪榴弹[S].北京:国防科学技术工业委员会,1989.

[3] 王益森,王怀军,宫小泽,等.GJB4225-2001 榴弹定型试验规程[S].北京:中国人民解放军总装备部,2001.

[4] 林元汇,刘可新,雷军,等.GJB4021-2000 步兵近战武器燃烧弹、发烟弹定型试验规程[S].北京:中国人民解放军总装备部,2000.

[5] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2014:82-94.

HAN Zi-peng.Exterior ballistics of projectile[M].Beijing:Beijing Institute of Technology Press,2014:82-94.(in Chinese)

[6] 胡良平.医学统计学[M].北京:人民军医出版社,2009:22-30.

HU Liang-ping.Medical statistics[M].Beijing:People’s Military Medical Press,2009:22-30.(in Chinese)

[7] 胡良平.面向问题的统计学—(1)科研设计与统计基础[M].北京:人民卫生出版社,2012:275-276.

HU Liang-ping.Problem-oriented statistics-(1) Scientific research design and statistical basis[M].Beijing:People’s Health Press,2012:275-276.(in Chinese)

[8] 浦发,芮筱亭.外弹道学[M].北京:国防工业出版社,1989.

PU Fa,RUI Xiao-ting.Exterior ballistics[M].Beijing:National Defense Industry Press,1989.(in Chinese)

[9] 闫章更,魏振军.试验数据的统计分析[M].北京:国防工业出版社,2003.

YAN Zhang-geng,WEI Zhen-jun.Statically analysis of test data[M].Beijing:National Defense Industry Press,2003.(in Chinese)

[10] MENDENHALL W.统计学[M].梁冯珍,译.北京:机械工业出版社,2009.

ResearchonTestMethodofFireConcentrationofSmallArmsGrenade

PU Li-sen,XU You-liang

(Baicheng Ordnance Test Center of China,Baicheng 137001,China)

To research the test method of ammunition concentration of small-arms grenades,the factors affecting the fire concentration,such as meteorological conditions,muzzle-velocity,fire angle and ballistic coefficient,were analyzed by combining the actual operation in the evaluation test of small-arms grenade.The critical factor affecting fire concentration was found.Based on the statistic theory,the variance checking-model was established.The testing results show that the ammunition temperature has no effect on fire concentration,and the adverse effect caused by accidental reason can be eliminated by grouping test.To ensure the uniformity of test conditions,the fire-concentration test should be divided into three groups under standard temperature.

small arms grenade;concentration test;variance checking-model;standard temperature

R826.6

A

1004-499X(2017)04-0048-04

2017-06-18

蒲利森(1977- ),男,高级工程师,硕士,研究方向为步兵榴弹及特种弹药鉴定试验。E-mail:sunny.laopu@163.com。