利用火焰弯曲理论预测复合推进剂侵蚀函数的方法与应用

陈 军

(南京理工大学 机械工程学院,江苏 南京 210094)

利用火焰弯曲理论预测复合推进剂侵蚀函数的方法与应用

陈 军

(南京理工大学 机械工程学院,江苏 南京 210094)

固体火箭推进剂的侵蚀函数目前还没有方便而有效的手段(无论理论方法还是实验手段)来获取,火焰弯曲理论能较好地揭示固体复合推进剂侵蚀燃烧现象,以此为基础,建立了火焰弯曲理论侵蚀函数方程,进一步求解得到随燃气流速变化的侵蚀函数。通过实例验证,该获取侵蚀函数的方法及获取的侵蚀函数具有较高的预示精度,满足工程计算要求,对于研究固体推进剂的侵蚀燃烧理论、获取固体火箭发动机侵蚀函数,以及提高固体火箭发动机内弹道预示精度,均具有重要的实际应用意义,该方法仅适用于AP复合推进剂。

内弹道;固体火箭发动机;固体推进剂;侵蚀函数;侵蚀燃烧

内弹道是固体火箭发动机的重要性能,人们从不同角度研究它,试图提高其预示精度,如提高维度(零维到一维,甚至多维)[1]、加入两相模型[2-3]等。而固体推进剂的侵蚀燃烧是影响固体火箭发动机内弹道性能的重要因素,同时也是燃烧学的重要研究方向。但是,侵蚀函数的准确获取是很困难的,一方面是侵蚀燃烧现象的研究还很有争论,另一方面还缺少方便而有效的实验手段来测量。本文以文献[4]中提出的用于预示AP复合推进剂侵蚀燃速的火焰弯曲理论为基础,发展了一种能够预测固体(AP复合推进剂)火箭发动机侵蚀函数的理论方法。

1 利用火焰弯曲理论预测固体火箭推进剂侵蚀函数的理论模型

根据火焰弯曲理论,AP复合推进剂的燃速可表示为[5]

(1)

(2)

由侵蚀函数的定义[6],可得侵蚀函数ε为

(3)

根据火焰弯曲理论,火焰弯曲角θ可表示为[5]

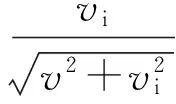
(4)

式中:v为平行于推进剂装药燃烧表面的燃气流速;vi为推进剂燃烧时的质量加入速度。

式(3)表明,从火焰弯曲理论导出的侵蚀函数主要考虑的影响因素为燃气流速v,同时还考虑了压强p、推进剂性质等因素的影响。

2 火焰弯曲理论侵蚀函数方程

由推进剂燃烧理论可知,推进剂燃烧时的质量加入速度vi为[7]

(5)

式中:ρp为推进剂装药密度;ρ为燃气密度;RT0为推进剂的火药力;a和n分别为推进剂的燃速系数与燃速压强指数。

将式(4)代入侵蚀函数表达式(3)中,整理可得:

将式(5)代入上式,可得关于侵蚀函数ε的方程为

[(K3p2)2-1]m2ε6+[2(1+K2)m-m2b2-2m(K3p2)2]ε4+
[(K3p2)2+2(1+K2)mb2-(1+K2)2]ε2-
(1+K2)2b2=0

(6)

如果视ε2为待求变量,则方程(6)为一元三次方程。由于该方程是从火焰弯曲理论推导得出的,可以称之为火焰弯曲理论侵蚀函数方程。该方程中系数b2包含了燃气流速v,因此,求解该方程可以得到不同流速v下的侵蚀大小,即可以得到ε-v的变化关系。

3 火焰弯曲理论无侵蚀燃速公式的求解

在求解火焰弯曲理论侵蚀函数方程(6)之前,需要先拟合得出所研究固体火箭推进剂无侵蚀燃速式(2)中的系数K1,K2和K3。

以某中口径固体火箭发动机复合推进剂为例,其无侵蚀燃速为

(7)

拟合分析得到相应系数为K1=0.811 4,K2=26.550 3和K3=0.125 1。因此,得到所研究固体火箭推进剂对应的火焰弯曲理论无侵蚀燃速公式为

(8)

式(8)中压强p的单位为MPa。

表1 各观测点拟合残差

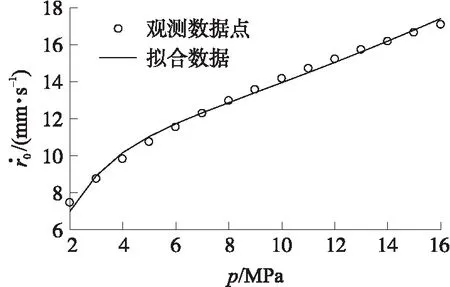
图1 燃速拟合曲线比较

4 火焰弯曲理论侵蚀函数方程的求解

求解火焰弯曲理论侵蚀函数方程(6)的目的是为了得到侵蚀函数ε-v的变化关系。求解该方程可以直接利用MATLAB求解一元三次方程的函数roots()。

取不同流速v(0～300 m/s),得到不同流速对应的侵蚀大小,结果参见表2。最后通过拟合得到ε-v的变化关系,如图2所示,即:

ε=0.986 4+0.001 2v

(9)

表2 预测得到固体火箭推进剂侵蚀与燃气流速的对应关系

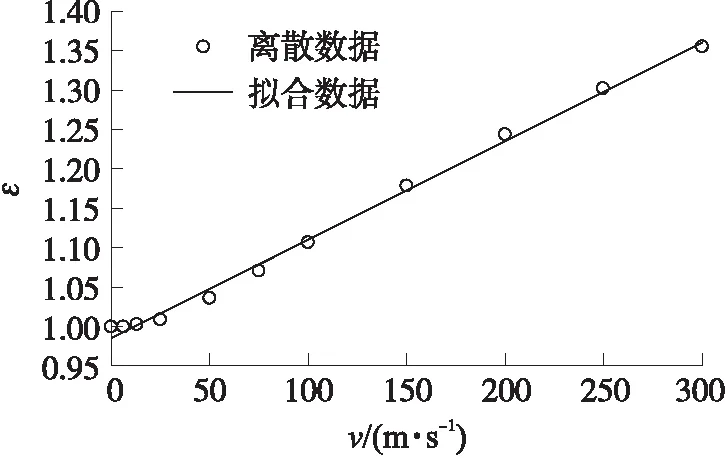
图2 预测得到某固体火箭推进剂侵蚀与燃气流速的拟合曲线

5 预测侵蚀函数的分析处理

通过求解火焰弯曲理论侵蚀函数方程(6)可以预测得到固体火箭推进剂的侵蚀函数,即式(9)。为检验预测得到的侵蚀函数是否正确,可以与现有的侵蚀函数进行比较分析。

该固体火箭推进剂的侵蚀函数为

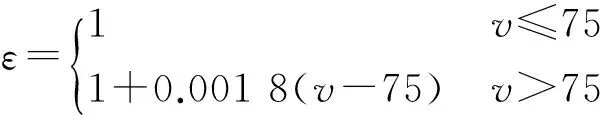
(10)

为方便比较,对上式进行线性拟合,可得该固体火箭推进剂侵蚀函数的拟合曲线为

ε=0.956 6+0.001 4v

(11)

比较式(9)和式(11),最大误差为3.12%(v=0时),最小误差为2.2%(v=300 m/s时),小于一般工程上的误差要求,因此,该预测侵蚀函数是可以应用工程计算的。

在应用之前,还需解决临界侵蚀流速的问题。从原侵蚀函数式(10)可知,该火箭推进剂的临界侵蚀流速vth=75 m/s,而火焰弯曲理论预测的侵蚀函数式(9)还没有这一数值形式。为此,还需要预先确定一个临界侵蚀流速vth(可参考相近火箭推进剂确定,这里取vth=75 m/s)。假设侵蚀函数式(9)可表示为

(12)

式中:ε′即为变换后形式上如式(10)的侵蚀函数,α为待求系数。采用曲线积分面积相等的原理进行变换,就可以得到待求系数α,即使得:

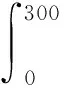
式中:ε为预测侵蚀函数,如式(9)所示。将式(9)和式(12)代入,则可得:

积分上式,可得待求系数α=0.001 97。因此,利用火焰弯曲理论预测的侵蚀函数为

(13)

预测的侵蚀函数与原侵蚀函数式(10)相比,最大误差为2.7%(v=300 m/s时),而当v<300 m/s时,误差逐渐减小。

6 利用火焰弯曲理论预测侵蚀函数的应用分析

上述过程可以完全确定一个固体火箭推进剂的侵蚀函数。该方法是否具有通用性,下面再以某小口径固体复合推进剂火箭发动机为例来说明。

首先,拟合出火焰弯曲理论无侵蚀燃速公式中的系数K1,K2和K3,得到对应的火焰弯曲理论无侵蚀燃速公式为

(14)

式中:压强p的单位为MPa。

其次,求解火焰弯曲理论侵蚀函数方程(6),得到侵蚀函数ε-v的变化关系为

ε=0.986 6+0.001 1v

(15)

最后,通过变形得到利用火焰弯曲理论预测的侵蚀函数(临界侵蚀流速vth=90 m/s是参考前面中口径火箭发动机的数值,经过尺寸效应修正得到的)为

(16)

该侵蚀函数应用于内弹道计算的结果如图3所示,图中t为工作时间。

图3 利用预测侵蚀函数计算的某固体火箭发动机工作压强曲线与实验数据的比较

表3 利用预测侵蚀函数计算的某固体火箭发动机工作压强与实验数据的比较

7 结论

通过2种固体复合推进剂火箭发动机的数据分析与应用,说明利用火焰弯曲理论预测固体火箭推进剂侵蚀函数的方法是可行的。该方法的主要过程包括3步:

①已知待研究固体火箭复合推进剂的基本燃速,拟合出火焰弯曲理论无侵蚀燃速公式的系数K1、K2和K3,即首先确定出火焰弯曲理论无侵蚀燃速公式;

②建立火焰弯曲理论侵蚀函数方程并求解该方程(本质上为一元三次方程),得到侵蚀函数ε-v的变化关系;

③确定临界侵蚀流速,采用曲线积分面积相等的原理对方程进行变形得到标准形式的侵蚀函数。

在建立该方法过程中,有几点需要说明:

①火焰弯曲理论定义火焰弯曲角θ时利用了固体推进剂垂直加入速度vi的概念。在利用该方法确定侵蚀函数时发现垂直加入速度vi的数值太小,即火焰弯曲角θ过小,夸大了侵蚀程度。为此,引入垂直加入速度vi的修正系数αi。该方法结合某中口径固体火箭发动机的数据给出αi=40,具有良好的通用性。

②该方法没有给出临界侵蚀流速vth的确定方法,虽然通过火焰弯曲角可以分析出vth的大小,但得出的数值偏小,不具有实用意义。该方法参考已知某中口径固体火箭发动机直接给出vth=75 m/s。

③对于不同尺寸的固体火箭发动机,采用侵蚀函数的尺寸效应原理[1],对上述修正系数αi和临界侵蚀流速vth进行尺寸效应修正,即(vi)b=(Da/Db)0.2(vi)a,(vth)b=(Da/Db)0.2(vth)a。其中尺寸效应采用的尺寸D为发动机外径;下标a,b表示2种不同尺寸的发动机。

该方法存在如下不足,需要进一步研究:

①只适用于AP复合推进剂,这是因为火焰弯曲理论只适用于AP复合推进剂。

②该方法只得出了ε-v的侵蚀函数,能满足固体火箭发动机一维内弹道计算分析的需要。其他因素如压强、推进剂性质等还需要深入研究。

[1] 陈军,封锋,余陵.固体火箭发动机一维两相内弹道研究[J].弹道学报,2010,3(22):16-20.

CHEN Jun,FENG Feng,YU Ling.Research on one-dimensional two-phase internal ballistics of SRM[J].Journal of Ballistics,2010,22(3):16-20.(in Chinese)

[2] 陈军.火箭喷管两相流动性能计算公式[J].弹道学报,2012,24(1):69-74.

CHEN Jun.Properties’ formulae of rocket nozzle with one-dimensional two-phase flow[J].Journal of Ballistics,2012,22(3):16-20.(in Chinese)

[3] 陈军.固体火箭发动机零维两相内弹道研究[J].弹道学报,2013,25(2):39-43.

CHEN Jun.Research on zero-dimensional two-phase internal ballistics of SRM[J].Journal of Ballistics,2013,25(2):39-43.(in Chinese)

[4] KING M K.A model of erosive burning of composite propellants[J].Journal of Spacecraft and Rocket,1978,15(5):139-146.

[5] 陈军,王栋,封锋.火箭发动机燃烧基础[M].北京:北京航空航天大学出版社,2015:318-319.

CHEN Jun,WANG Dong,FENG Feng.Principles of solid rocket motors combustion[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2015:318-319.(in Chinese)

[6] 武晓松,陈军,王栋.固体火箭发动机原理[M].北京:兵器工业出版社,2015:60-64.

WU Xiao-song,CHEN Jun,WANG Dong.Principles of solid rocket motors[M].Beijing:Ordnance Industry Press,1996:60-64.(in Chinese)

[7] 武晓松,陈军,王栋.固体火箭发动机气体动力学[M].北京:北京航空航天大学出版社,2016:132-134.

WU Xiao-song,CHEN Jun,WANG Dong.Gas dynamics of solid rocket motors[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2016:132-134.(in Chinese)

[8] 温欣研.Matlab R2016a从入门到精通[M].北京:清华大学出版社,2017.

WEN Xin-yan.Matlab R2016a from entry to mastery[M].Beijing:Tsinghua University Press,2017.(in Chinese)

ApproachandApplicationofPredictingErosiveRatioofCompositePropellantBasedonFlameBendingTheory

CHEN Jun

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

There is no convenient and effective means(both theory and experimental means)to obtain erosive ratio(erosive function)of solid rocket propellant.The Flame Bending Theory(FBT)can better reveal the burning erosion phenomenon of solid propellant.On this basis,the FBT erosive ratio equation was established,and further the erosive function varying with the combustion gas flow was obtained from the equation.Through the examples,the method of obtaining erosive function and the obtained erosive function have very high prediction precision and meet the requirements of engineering calculations.The method has important practical application significance to research erosion combustion theory for solid rocket propellant,acquire erosive function of solid rocket motor,and improve the prediction accuracy of internal ballistics of solid rocket motor.This method is only suitable for AP composite propellants.

internal ballistics;solid rocket engine;solid propellant;erosive ratio;erosion combustion

V435

A

1004-499X(2017)04-0081-05

2017-07-21

陈军(1969- ),男,副教授,博士,研究方向为新型推进技术研究。E-mail:cjsky123@njust.edu.cn。