“研学后教”理念下的中学数学单元教学的策略研究
谷新婷
[摘 要] “研学后教”理念对初中数学课堂的优化有着很好的启发意义,本文以“研学后教”理论为指导,立足于初中数学单元教学,指出教师在教学中应研究学生的学习规律,引导学生自编习题,且理性地对待学生的错误.
[关键词] 研学后教;初中数学;教学策略
当前的初中数学课堂倡导充分发挥学生的自主性. 在此背景下笔者认为,将“研学后教”理念运用于初中数学的单元教学中,有助于课堂效率的提升.
“研学后教”理论与初中数学 课堂
“研學后教”理论是新课程改革不断推进和发展过程中的重要产物,该理论要求教师在教学中有效地定位“学”与“教”之间的关系,由此更新自己的师生观和教学观,并将该理论积极运用于教学,让课堂教学更加匹配学生发展的实际需要.
以“研学后教”理论来建构初中数学课堂时,教师在教学之前要充分做好“研学”工作,即教师要深刻研究学生的知识基础、学法特点,同时要立足于学生的视角来分析学习材料,设计各种学习活动,探求适合学生的学法指导思路. 另外,教师还要精心编写学案,指导学生自主“研学”,并在合作探究中突破学习难点;在学生进行交流互动的过程中,教师要恰当地进行点拨和启发,引领学生展开更进一步的探究,从而达到教学目标.
“研学后教”理论指导下的初中数学单元教学策略
单元教学是当前初中数学教学的主要形式,如何从“研学后教”的理论出发精心组织教学,由此提升效率呢?笔者认为,除了平时最常见的有机整合单元内容,将零散的知识连成知识网络等方法而外,还可以在“研学后教”理念指导下从以下几个方面着手.
1. 研究学生的学习规律,优化其思维品质
苏霍姆林斯基指出:“在人们的内心深处,大家都渴望让自己成为一个研究者、探索者和发现者. ”结合初中生的学习特点我们可以发现,很多学生喜欢对一些新鲜而奇怪的问题发起挑战. 进行初中数学单元学习时,很多学生在思维过程中暴露出了这样的问题:他们过分关注问题的最终结果,忽视探究过程本身. 为此,教师要引导学生积极而主动地研究学习规律,进而在自己的反思行为中发现存在的问题,并由此促进问题的解决. 问题往往可以让学生将自己的认识推向更深的层次,我们可以引导学生进行自发提问:“为什么要如此研究?是否存在我们没有考虑到的情况?还需要用什么方法来进行检验或求证吗?”这些操作有助于学生反复思考自己的学习过程,进而将思维提升到更加开阔而深刻的程度.
例题?摇 2017年5月,勒索病毒席卷全球,这种病毒的传播速度非常快. 假如一台计算机被病毒感染,那么在两轮感染后将会有81台计算机被感染. 请结合数学知识分析一下,每轮感染中平均每台计算机将感染多少台计算机.
这个问题衍生于2017年的网络关键词“勒索病毒”,以此为情境来引导学生探索,很容易激起学生的兴趣. 教师将这个问题提供给学生,让他们先自行研究,同时提醒学生不能只关注答案是什么,关键是要弄清楚思路探寻的过程.
以下是学生在交流过程中给出的答案:假设每一轮一台计算机将感染x台计算机,结合题意可得方程1+x+(1+x)x=81. 这是一个学生都比较熟悉的一元二次方程,但如果仅止于将答案解出,这个问题便没有多少价值,那怎样才能引导学生更加深入地展开分析与思考呢?笔者认为,应该引导学生先进行观察,并尝试对方程进行变形处理,即提取公因式(x+1)后,方程变成(1+x)2=81,在此基础上,教师继续提出问题:如果经过三轮感染,那一共有多少台计算机被感染?请用含有x的表达式表示. 如果经过n轮呢?
学生展开思路,写出计算式(1+x)2+x(1+x)2,并通过化简指出第三轮被感染计算机的台数为(1+x)3,在此基础上,学生也能形成结论:经过n轮,被感染计算机的总台数应该为(1+x)n. 当学生自认为问题已经完全解决时,笔者再抛出一个新的问题:“现实情形下,往往不止一台计算机被感染,原题中‘假如一台计算机被病毒感染这一条件变成‘假如2台计算机被病毒感染,那问题又该如何处理呢?”学生经过分析,形成了结论:三轮之后被感染计算机的总台数应该是2(1+x)3,经过n轮,被感染计算机的总台数应该为2(1+x)n. 笔者再次提出问题:“原题中的条件变成‘假如n台计算机被病毒感染,那么问题又该如何处理呢?”学生的思维再次被问题驱动,形成更加深刻的认识. 最后,笔者列举出细胞分裂、银行复利等问题,由此引导学生展开分析和比较,进而明确此类问题的相似之处.
以上例子是一元二次方程的应用,是整个“一元二次方程”单元的教学难点. 不少教师认为让学生记住口诀“原量×(1±百分率)n=新量”,学生就能解决问题,结果,学生经常记错公式或由于不理解公式而无从入手,根本不能达到教师的期望. 上述问题的设计隐含着整合单元知识的思想,能引导学生用同样的思维方法解决同类问题;同时,这些问题都是在对学生思维特征进行充分研究的基础上提出的,而学生在这些问题的启发下展开更加深入的思考,他们的思维水平就会得到更深层次的提升和发展. 学生理解了上述问题的解决办法,就不需要记忆任何公式,遇到类似问题,也能用同样的方法解决.
2. 指导学生自编练习,激活他们自觉学习的意识
综观当前的数学教材我们发现,教材上所配习题相对较少,结合整个单元的知识设计的题目更少,而且梯度不强. 而如果由教师进行组题、编题,作业的统一性又太强,很难适应每个学生的学习需要. 在研究学生学情的时候我们还发现,学生在面对常态化的数学作业时,总提不起精神,这说明如果我们始终以现成习题的方式来组织学生进行课后作业,那效果将无法得到切实的保障. 怎样改变这一情况呢?笔者认为,在新型的单元教学过程中,教师可以指导学生自行拟定习题,以此来检查自己的学习水平. 学生在自编习题时,会把视线集中在自己的认知难点,在打磨习题的过程中必然会对相关知识或技能进行反复咀嚼,这一过程必然导致学生进一步熟悉有关知识和方法,而且这也会对学生创新思维的发展产生促进作用.
在学生自拟习题的时候,我们可以安排学生以学习小组为单位,相互出题与检测,然后相互交流出题、做题的心得,相互促进,共同成长. 这样可以让学生的自主学习更具交互性,而且相互出题有助于学生变换思考问题的视角,可由此提升他们的认识. 比如学习“反比例函数”之后,学生在自编习题时,就编出了以下两道习题.
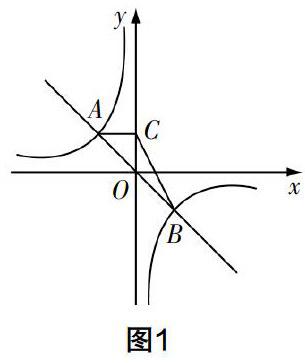
自编习题1?摇 函数y=-x和y=-4/x的图像交于A,B两点(如图1),过点A作y轴的垂线AC,C为垂足,连接BC,求△BOC的面积.
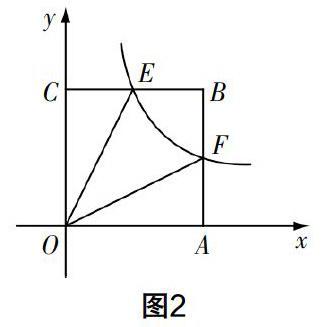
自编习题2?摇 已知双曲线y=k/x(x>0)经过矩形OABC的边AB和BC的中点F,E(如图2),且四边形BFOE的面积为2,请确定k的取值.
以上两道题都涉及反比例函数知识,但考查的侧重点不同,体现了题目的灵活多变性,避免了教师命题的单一性.
3. 理性对待错误,在纠错中促进发展
“研学后教”理论倡导将学生推向知识探究的最前沿,这样的操作必然导致学生在学习过程中发生很多错误. 面对这些错误,教师一方面不能过分苛责学生,另一方面也不能不管不顾. 教师要指导学生理性面对这些错误,合理而正确地展开分析和探索,让学生在错误纠正的過程中实现发展.
比如学生在研究用平方差公式进行因式分解时,遇到了这样一个问题:分解因式x4-y4. 笔者在巡查的过程中发现,一部分学生的答案是(x2+y2)(x2-y2). 面对学生的错误,笔者没有立即评价,而是让学生自行观察和比较. 学生很快就发现了问题:因式分解要彻底,既然(x2-y2)还可以分解,就需要继续分解. 在这个处理错误的过程中,教师切不可因学生暴露问题而生气,当然,也不可急切地纠正错误,我们应该将主导权移交给学生,让他们在进一步的观察与思考中形成更加深刻的认识,这才是“研学后教”理念指导下的有效教学!
面对学生的错误,教师的耐心与宽容显得非常重要,当然,学生自己的心态也很重要. “研学后教”的教学过程本身应该是一个知识探索的过程,学生只有不断地进行假设、论证,他们的认识才会不断深化,方法和技巧才会逐渐成熟.
当我们将“研学后教”理念与初中数学单元教学进行融合时,数学教师要加强学习和反思,同时要结合学生的反馈来总结经验教训. 只有这样,我们才能在实践中不断地进步和提升,课堂才会更加精彩.

