关注学生起点 落实有效教学
徐佳梅


[摘 要] 着眼于学生认知与思维、已有方法与经验、经历等学习起点进行设计与教学,能更加充分地激发学生学习的自主性与学习探究的热情,因此,教师在具体教学中应不时关注学生学习的起点,并善于在学生起点处进行各种有意义的设计与落实.
[关键词] 起点;认知;思维;方法;经验;经历;有效教学
大多数教师在平时的教学中都会根据自己预先准备的教案设计按部就班地完成课堂教学,教学目标也尤其现实地仅仅围绕预设目标,这种严重忽略学生主动性与创造性的机械化教学对学生数学思维的发展极为不利. 数学是思维的体操,在课堂教学中注重发展学生的数学思维能力,提升学生的数学素养,才是数学教学最应该关注的内容. 因此,教师在平时的课堂教学中不仅不能忽视学生这一学习主体,还应在具体的教学中将学生主体凸显出来,以促进他们数学素养的全面发展. 下面,笔者用具体例题表达自己在数学教学中的一点体会.
如图1,在△ABC中,D为BC上一点,∠1=∠2,BD=CD,求证:AB=AC.
这是教材上的一个例题,笔者在此题的教学分析中比较关注学生的认知与思维起点,着眼于学生思维能力的提高,于是与学生一起进行了例题的解析.
1. 环节1:着眼于学生的认知与思维起点,激发学生的认知冲突与探求欲望
此阶段的学生已经基本掌握了等腰三角形的判定与性质、全等三角形的判定与性质、逆命题、真假命题、图形运动等知识与定理,学生懂得在AB=AC时,已知①∠1=∠2,②BD=CD,③AD⊥BC这三个条件中的任何一个就可以得到其他两个,因此,笔者在此题的解析之初就着眼于学生已经掌握的等腰三角形知识抛出了下列问题:如果从①②③这三个条件中任意选出两个作为题设,能够得到AB=AC这一结论吗?学生联想逆命题的相关知识很快得出了三种情况,运用全等三角形的知识对其中两种情况进行了证明. 不过,当①②两条件作为题设时,原有图形中已知等量关系的“SSA”结构却无法判断△ABD与△ACD全等,于是AB=AC这一结论也就无法说明了. 学生原有的知识与经验对于这一问题的解决,明显不够,认知冲突自然产生的同时也将学生的求知欲望激发了出来:如果将②③作为已知条件,是否能得到AB=AC呢?笔者关注到了学生的疑问与思考,并及时提出了以下建议:大家可曾想过借助几何画板来判断这一命题的真假呢?大家可以在图形的运动中得到符合条件①②的△ABC,度量出AB和AC的长度后,再比较它们是否相等. 学生在教师的启发之下很快投入到了积极而热烈的讨论与交流中:在∠MAN的平分线AE上任取一点D,过点D作直线BC与AM,AN分别交于B,C两点,在交点B,C运动的过程中显示BD,DC,AB,AC的度量值. 在点的运动中我们可以直观观察到:当BD≠DC时,AB≠AC;只有当BD=DC时,AB=AC. 由此可见,将①②作为题设确实能得到AB=AC这一结论. 具备一定质疑意识的学生此时不禁纳闷:证明AB=AC又有什么用呢?顺着学生的这一疑惑,后续例题解析的呈现也就水到渠成了.
笔者紧接着以学生的原有知识基础对等腰三角形、全等三角形知识进行了复习,后续问题的解决也因为前面例题的讨论获得了很好的方法思考. 借助逆命题渗透问题形成的方法,也在关注学生认识与思维起点的教学中得以实现.
2. 环节2:着眼于学生已有方法这一起点,引导学生自主探究
此阶段的学生已经掌握了利用全等三角形的性质、等腰三角形的判定来证明线段的一些方法,但因为之前的尝试在此题的解决中不起作用,因此从AB=AC这一结论出发进行证明,是行不通的. 因此,学生转换角度并着眼于条件开始尝试. 学生面对∠1=∠2这一已知条件进行了以下思考:一个角关于角平分线呈轴对称,可以将其翻折. 笔者关注到学生的这一思考并适时抛出问题:大家从角平分线上有没有联想到什么图形呢?学生很快意识到图形中有轴对称图形. 笔者顺着学生的思维又抛出问题:大家可否从轴对称图形上联想到什么操作运动?(翻折)怎样翻折呢?通过翻折来说明AB=AC又该怎样进行呢?笔者提出这些问题正是基于学生已有翻折这一实践活动经验而做出的考虑. 学生在问题的启发下很快想到沿角平分线AD进行翻折的实践操作,但解释B点与C点重合时却又产生了新的问题:已知条件中并没有告诉我们∠ADB,∠ADC是否相等,B,C,D这三个点是否在同一条直线上也就无法说明了. 因此,借助角平分线的知识来解决此题也行不通.
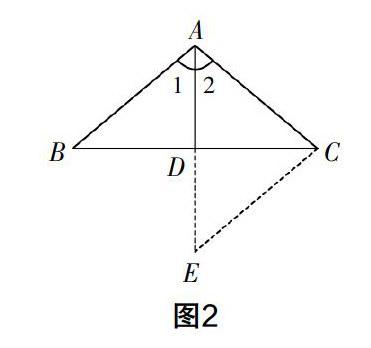
从前面一个条件出发来解决问题已经行不通,学生也就自然会再考虑第二个问题“BD=CD”. 借助角平分线知识虽然无法解决问题,但学生却在这一阶段的思考中获得了图形运动的思路,因此,笔者赶紧结合学生的这一认知,以及题中所给的中点这一条件启发学生:大家看到点D为线段BC的中点这一条件了吗?看到这一条件,大家可曾联想到什么操作?(旋转)学生的反应很快,但紧接着却发现线段BD绕点D旋转180°后点B和点C是能够重合的,看上去跟AB,AC没有联系. 笔者关注到学生的思维发展后追问:点A能不能纳入这一旋转过程呢?学生的思考在教师的这一问题下变得更加深入:可以将△ABD绕点D旋转180°得到△ECD,AB和AC就融進了同一个三角形中. 不仅如此,∠1与∠2本来是在两个小三角形中的,现在都在△CAE中了(如图2). 根据等角对等边可知AC=EC,因此AB=AC,问题获解.
笔者在探究证明思路的解析过程中一直关注学生已经掌握的方法,并对学生的讨论、交流进行了有效的引导和组织,解题思路也得到了很好的渗透:从待证结论或已知条件都可以进行一定的考虑,以证明几何问题,如果行不通,应赶紧联想已知相关知识与已有解题方法.
3. 环节3:着眼于学生已有经验这一起点,引导学生自主反思
学生从失败到成功的探究体验中积累了问题形成、利用中点进行旋转解决相关问题等经验,笔者在学生已具备的抽象思维与概括能力的基础上又抛出了以下问题:(1)尝试运用旋转这一操作,一般在出现什么样的已知条件时可以运用呢?(2)大家以为在此题的解决中将图形进行旋转是为了什么呢?这些问题能促进学生自主反思与总结. 很快,学生的思维产生了碰撞,并进行了总结:图形中出现对称图形时可以考虑旋转这一操作,图形重合的现象就会因此产生. 本题中的已知条件与待证结论在图形的旋转下得到了新的分布,待证结论和已知条件之间的距离因旋转而得到了有效缩小,所以促进了问题顺利解决.
学生的总结将学生在具体经验中进行抽象概括的水平充分展现了出来,结论以及知识发生的过程都在概括中得到了完美体现.
4. 环节4:着眼于学生已有经历这一起点,设计反馈练习
学生的小结以及解题探究过程在笔者的心里留下了极为深刻的印象,因此,笔者在本课的教学结尾阶段,结合学生的认知状态,进行了以下课堂反馈练习设计.
练习1 如图3,已知∠BED=∠DAC,BD=CD,求证:BE=AC.
练习2 如图4,在△ABC中,BD=CD,BF与AC,AD分别交于点F和点E,且AF=EF,求证:BE=AC.
练习3 如图5,在△ABC中,∠BAD=∠DAC,BM=CM,过点M作AD的平行线与AB交于点E,与CA的延长线交于点F,求证:BE=CF.
已知一边的中点,并能通过图形的旋转求证结论是这三个练习题共同的特征. 实际上,这是基于本课例题所做的变式. 学生在不同程度的变式中进行循序渐进的思考,学习参与的“广度”与“深度”都得到了很好的保障,学生在不同程度的思考、探究与练习中对本课中所涉及的添线方法形成了牢固的掌握,认知与思维能力也在不同程度的思考中得到了有意义的锻炼.
事实上,教师在具体教学中能够不时关注学生的学习起点,并善于在学生起点处进行各种有意义的设计与落实,学生学习的自主性以及学习的热情、探究新知的欲望,必能得到极其充分的激发,并最终实现思维能力的提升.

