大粘滞摩擦因数的永磁伺服系统自适应反步控制*

吴 晶, 朱孝勇, 左月飞, 张 超, 全 力

(江苏大学 电气信息工程学院,江苏 镇江 212013)

大粘滞摩擦因数的永磁伺服系统自适应反步控制*

吴 晶, 朱孝勇, 左月飞, 张 超, 全 力

(江苏大学 电气信息工程学院,江苏 镇江 212013)

对于粘滞摩擦系数大的永磁伺服系统，传统的自适应反步控制会导致参数辨识结果波动较大、不易稳定、转速跟踪性能较差。设计了一种实时辨识粘滞摩擦因数的自适应反步控制器，同时对转动惯量、负载转矩和粘滞摩擦因数进行辨识，提高了对粘滞摩擦因数较大系统的转速跟踪性能和转动惯量及负载转矩辨识精度。所提方法结构简单、易于实现，在dSPACE公司的DS1103系统试验平台上对其进行了试验验证，试验结果表明了所提方法的正确性和有效性。

永磁同步电机；粘滞摩擦因数；自适应反步控制；转动惯量

0 引 言

永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)以其结构简单、运行可靠、高功率密度和高效率等优点，被广泛应用于工业机器人、精密数控机床和航空航天等伺服系统领域。其控制结构大多采用双闭环的PI控制器，但PI控制方法不仅对系统参数的不确定性敏感、抗干扰能力弱，而且对负载变化的适应能力不强；而PMSM作为伺服电机应用受到未知负载、摩擦等机械参数变化的影响，线性PI控制不能满足控制性能要求[1]。对此学者们研究了非线性PI控制[1-2]、滑模控制[3-4]、模糊控制[5-6]、神经网络控制[7]等现代控制算法，但这些控制策略存在系统抖振或算法较复杂等问题，因此需要研究更简单的控制方法。

反步控制理论在永磁伺服控制系统的应用引起了广泛的关注[8-12]。其根据系统控制目标，基于状态方程来反推出系统的输入，设计过程简单，且能保证系统的全局稳定性。文献[8]基于反步法设计控制器，与PI控制相比减少了调节参数数目，只需调节3个参数，其本质是保留了比例调节器而取消积分调节器，系统参数已知且不变时通过精确的静态补偿实现状态的无静差跟踪，具有较快的动态响应。

然而伺服系统经常运行于复杂的工况，系统参数经常发生变化，此时反步控制器会出现较大的稳态误差和动态误差，因此必须对未知参数进行准确地在线估计，与自适应控制相结合实现更好的参数鲁棒性。目前已有文献对系统参数进行辨识实现自适应反步控制。文献[13]对定子电阻和负载转矩进行辨识来提高系统抗干扰能力。文献[14]对负载转矩及粘滞摩擦因数实时辨识，为低速性能的改善提供了新的解决方法。文献[15]对电阻、负载转矩及摩擦因数进行准确辨识，更好地抑制参数变化对速度跟踪性能的影响。可见已有的反步文献主要对定子电阻、负载转矩及粘滞摩擦因数进行自适应辨识，考虑转动惯量变化对转速跟踪性能影响的文献很少。文献[16]设计了转动惯量和负载转矩自适应反步控制器，但设计过程中忽略了粘滞摩擦因数的影响，导致粘滞摩擦因数较大的伺服系统的参数辨识不稳定，影响转速跟踪性能。

本文同时考虑了影响伺服系统转速环跟踪性能的转动惯量、负载转矩及粘滞摩擦因数的变化，对三个参数同时辨识，实现自适应反步控制。首先给出了传统自适应反步控制器设计过程，分析了传统自适应反步未辨识摩擦因数对辨识结果的影响；接着推导了实时辨识粘滞摩擦因数的自适应反步控制器；最后在dSPACE公司的DS1103系统试验平台上对本文所提方法进行试验验证，试验结果表明了参数辨识准确、收敛速度快，说明系统具有良好的参数鲁棒性和转速跟踪性能。

1 PMSM数学模型

本文以交流伺服系统中通常采用的表贴式PMSM为研究对象。PMSM在转子磁场定向的同步旋转坐标系下的机械运动方程为

(1)

定子电压方程为

(2)

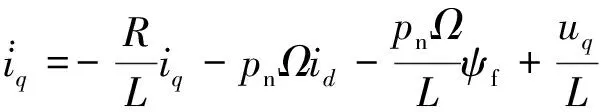
式中：J——系统的转动惯量，kg·m2；

B——系统的粘滞摩擦因数，N·m·s/rad；

TL——负载转矩，N·m；

Ω——机械角速度，rad/s；

Kt——转矩常数，N·m/A；

id、iq——d、q轴电流，A；

ud、uq——d、q轴电压，V；

pn——电机极对数；

ψf——永磁磁链，Wb；

R——定子电阻，Ω；

L——定子电感，H。

2 系统控制器设计

2. 1 传统的自适应反步控制器设计

永磁伺服系统的控制目标是速度跟踪，定义角速度跟踪误差e=Ω*-Ω，则跟踪误差状态方程为

(4)

取如下正定函数

(5)

对式(5)求导并令

(6)

式(6)表明，令de/dt=-ke(k>0)即可使系统渐近稳定，结合式(4)可得转速环的控制量为

(7)

为实现电流跟踪，定义iq和id的跟踪误差分别为eq=iq*-iq、ed=id*-id，电流跟踪误差的状态方程为

(8)

取如下正定函数

(9)

求导可得

(10)

令deq/dt=-k1eq、ded/dt=-k2ed(k1>0,k2>0)即可使系统渐近稳定，于是可得电流环的控制量ud、uq为

(11)

(12)

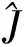
(13)

将式(7)中的参数J和TL分别用其估计值代替，则系统实际控制量为

(14)

将式(14)代入式(4)可得

(15)

取如下正定函数

(a>0,b>0)(16)

对式(16)求导可得

(17)

考虑到J及其估计值均始终为正数，因此式中的第一项始终是负数，只要令后两项为零，则可保证系统渐近收敛，于是参数的自适应律为

(18)

可得转动惯量和负载转矩的辨识公式为

(19)

由式(14)和式(19)可得传统自适应反步转速控制器结构框图如图1所示。转动惯量及负载转矩初始值在积分器中设置。参数k影响转速的跟踪性能，k越大，转速跟踪性能越好，但k不能无限增大，否则会导致噪声太大。自适应参数a、b取值太小容易导致参数辨识收敛速度慢，而取值太大则会使辨识结果振荡不收敛，需根据系统实际情况选取。

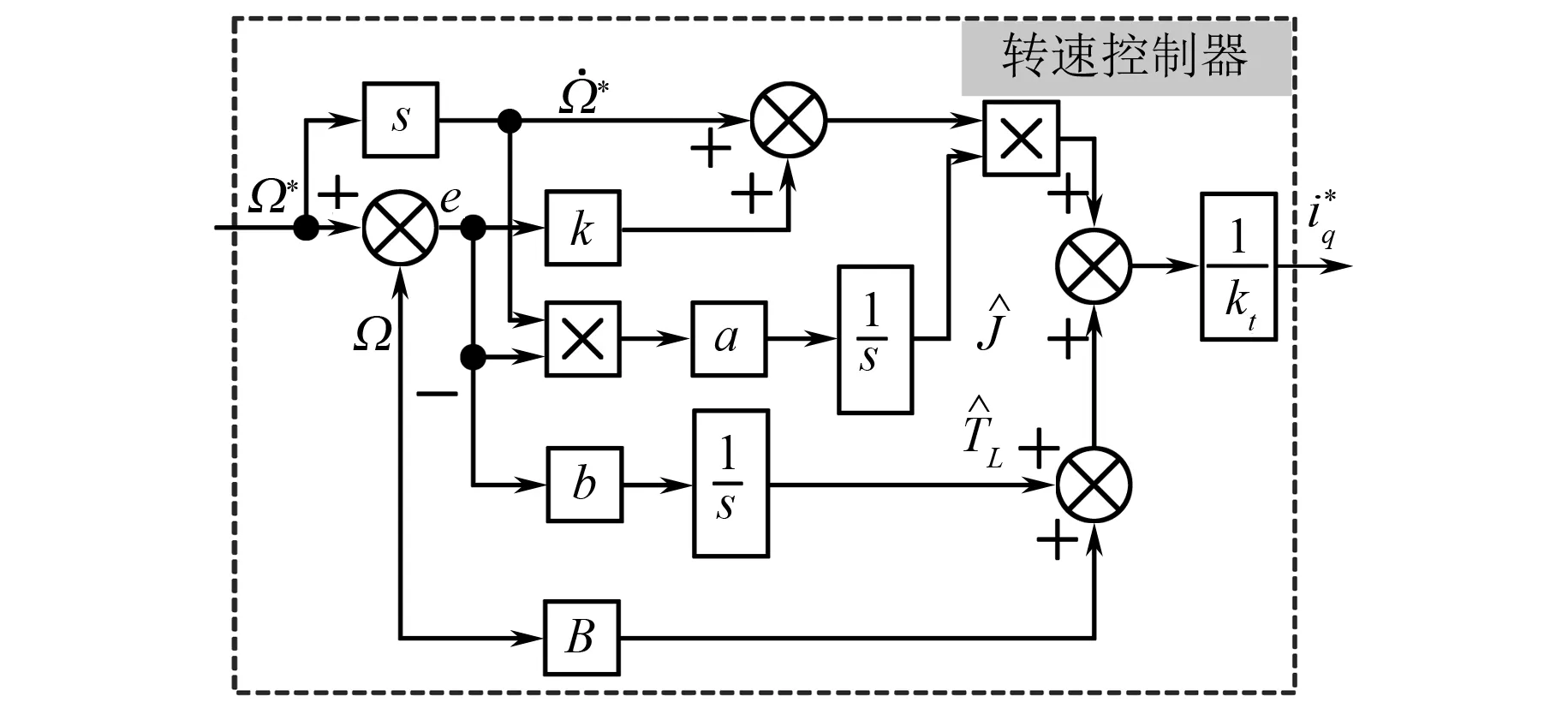
图1 传统的自适应反步转速控制器结构框图

此外，由电机运动方程可知，转动惯量J与角速度变化率d/dt以乘积的形式存在，只有角速度变化率不为零时才能辨识出J，因此试验中给定正弦转速。

2. 2 传统自适应反步控制器存在的问题

传统的自适应反步控制器把粘滞摩擦因数当成已知且不变，但实际伺服系统中粘滞摩擦因数B往往未知且容易发生变化，导致传统自适应反步转速控制器跟实际电机模型之间存在一个与摩擦力矩BΩ有关的误差。从式(19)的辨识公式来看，转动惯量和负载转矩辨识结果与模型误差有关。若系统粘滞摩擦因数较小则不会对辨识结果产生太大影响，但对于存在较大粘滞摩擦因数的伺服系统来说，未实时辨识粘滞摩擦因数的传统自适应反步转速控制器受摩擦项BΩ影响，导致辨识结果随速度变化而变化。试验中转速给定为正弦信号，导致转动惯量、负载转矩辨识结果产生较大的波动，影响转速跟踪性能。

3 实时辨识粘滞摩擦因数的控制器设计

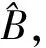
(20)

将式(7)中的参数J、TL和B分别用其估计值代替，可得系统实际控制量为

(21)

将式(21)代入式(4)可得

(22)

取正定函数

求导可得

显然式中的第一项始终是个负数，因此只要令后三项为零，即可保证系统渐近收敛，于是有

(25)

可得出转动惯量、负载转矩和粘滞摩擦因数辨识公式为

(26)

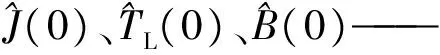
由式(26)可得实时辨识粘滞摩擦因数的控制器结构框图如图2所示。自适应参数c跟参数a、b取值原则一样，根据系统实际情况选取。

图2 实时辨识粘滞摩擦因数的控制器结构框图

4 试验验证

为验证本文方法的有效性，对PMSM伺服系统进行试验验证，所用PMSM参数如表1所示。

表1 电机参数

试验平台如图3所示。试验平台基于dSPACE公司实时仿真系统DS1103，逆变器开关频率为10 kHz，转速环和电流环采样周期及系统的计算步长均为0.1 ms。试验平台主要由DS1103、控制板、PMSM、联轴器及负载电机构成。试验系统存在较大的粘滞摩擦因数。由于电机按正弦转速给定，转速时刻在变化，不便于对系统施加额外的负载转矩，故试验中的负载转矩只由负载电机摩擦产生。

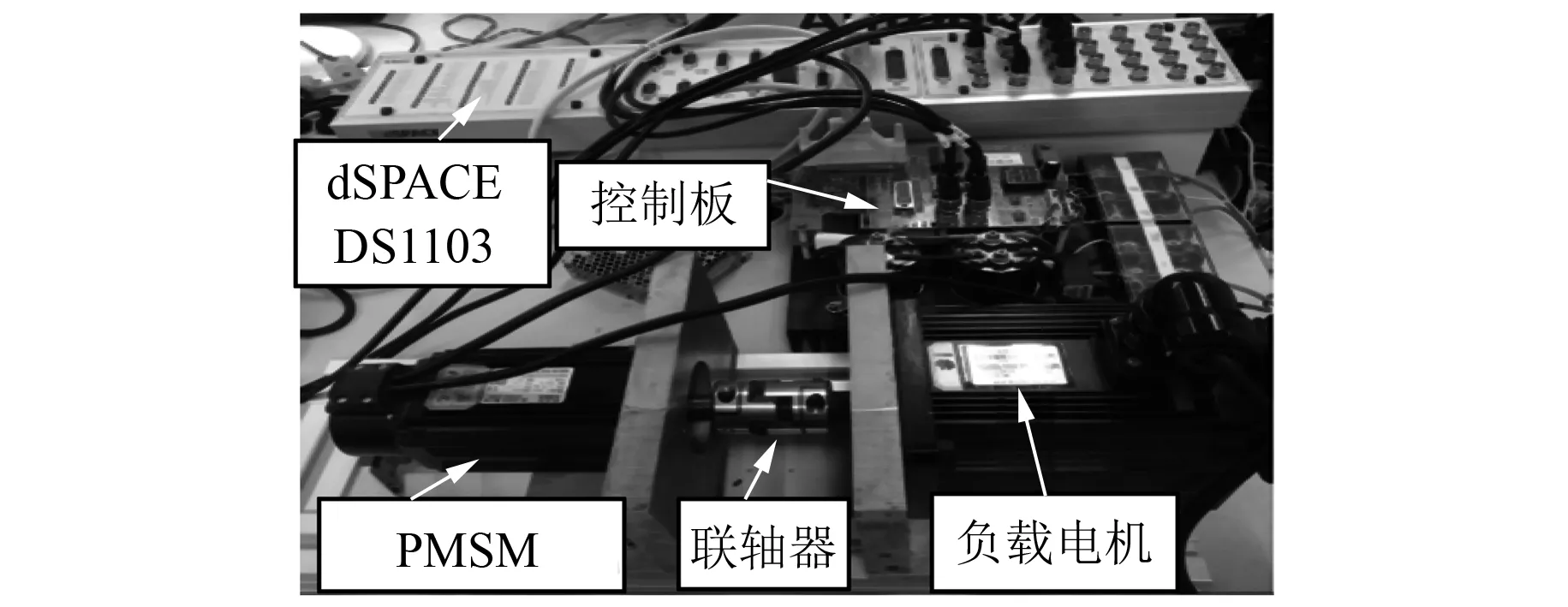
图3 试验平台

4. 1 传统自适应反步控制器的试验验证

给定转速为500 r·min-1/5 Hz的正弦信号，控制器参数设置k=80、a=1×10-6、b=1。转动惯量初值Jest(0)分别为1 g·m2和3 g·m2时的试验结果如图4所示。由图4的(a)、(b)可看出转动惯量辨识值在1.6～2.0 g·m2范围内波动，负载转矩估计值在-0.2～0.2 N·m内波动，辨识结果不准确，有明显的波动，验证了传统的自适应反步存在问题的理论分析的正确性。由图4的(c)、(d)可看出由于参数辨识值不准确，导致转速跟踪误差较大，为±40 r·min-1。

图4 传统自适应反步控制器的试验结果

4. 2 实时辨识粘滞摩擦因数控制器的试验验证

给定500 r·min-1/5 Hz的正弦转速，控制器参数设置k=80、a=1×10-6、b=1、c=0.000 5。转动惯量初值Jest(0)分别为1 g·m2和3 g·m2时的试验结果如图5所示。由图5的(a)、(b)可看出无论估计转动惯量初值大于或小于真实惯量值，惯量辨识值均稳定收敛至1.8 g·m2，惯量初值为3 g·m2时经过两个周期0.4 s，惯量即可收敛至真实值；惯量初值为1 g·m2时收敛速度更快，经过一个周期0.2 s即可稳定至真实值，负载转矩辨识值为0，粘滞摩擦因数经过0.5 s即可得到辨识值为0.012 N·m·s·rad-1。由图5的(c)、(d)可看出转动惯量在达到真实值前转速跟踪误差较大，一旦惯量收敛至真实值，那么转速跟踪误差则从±100 r·min-1减小到±10 r·min-1。

图5 跟踪500 r·min-1/5 Hz正弦转速的试验结果

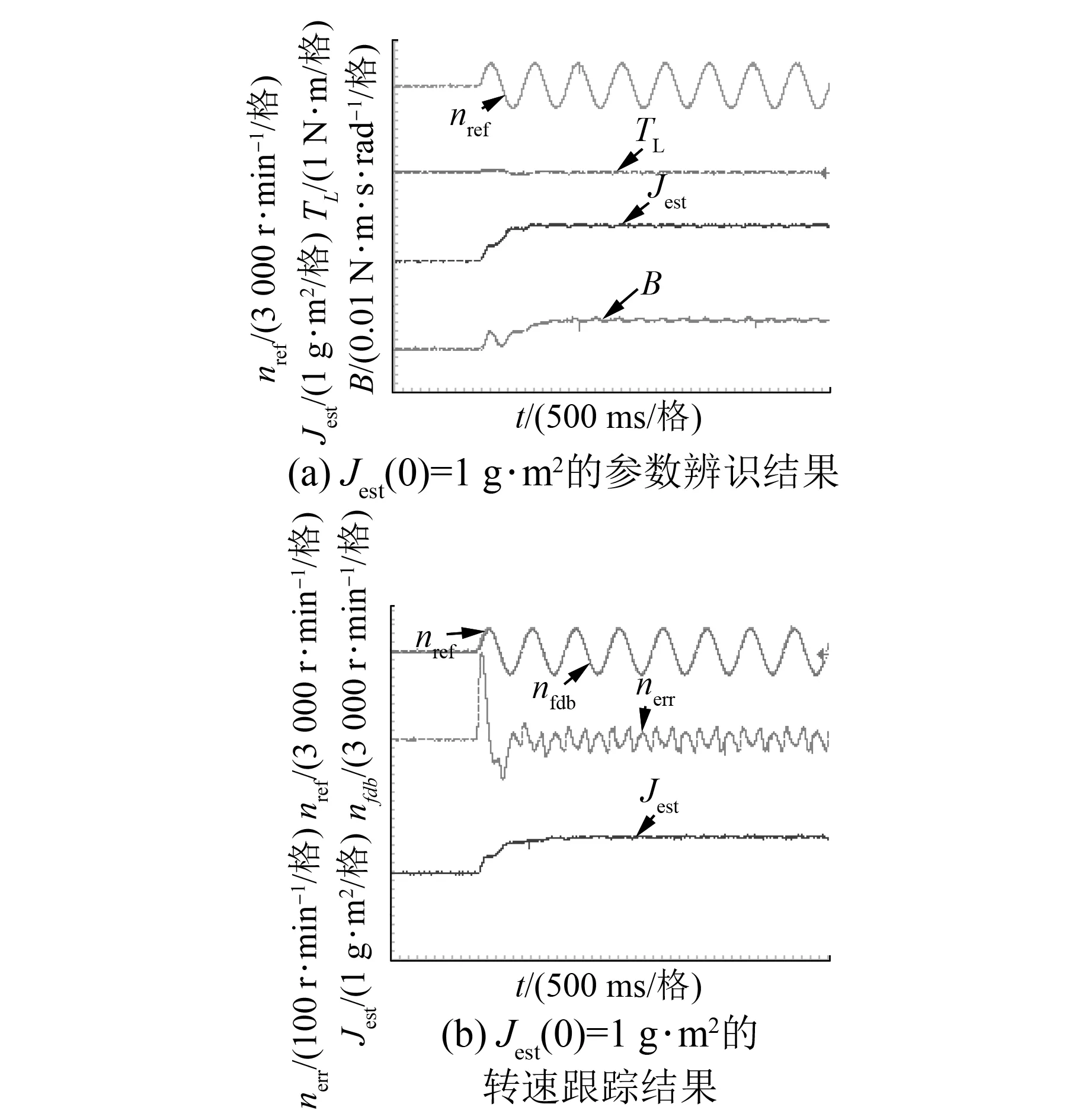
图6 跟踪1 500 r·min-1/2 Hz正弦转速的试验结果

改变电机转速为1 500 r·min-1/2 Hz，k=80、a=2×10-7、b=0.5、c=5×10-5。惯量初值Jest(0)为1 g·m2的试验结果如图6所示。可看出只需经过一个周期0.5 s，惯量即可收敛至1.8 g·m2，负载辨识值稳定至0，粘滞摩擦因数经过1 s可收敛至0.006 N·m·s·rad-1。一旦惯量收敛至真实值，转速跟踪误差减小到±20 r·min-1。

图5和图6表明，本文所提算法能在不同转速幅值及频率和不同初始惯量值同时实现转动惯量、负载转矩和粘滞摩擦因数的准确辨识，且转速跟踪误差小，验证了本文设计方法的正确性和有效性。

让电机以恒定转速运行，空载测量q轴电流值，以转速n为横坐标，转矩Te为纵坐标，可得图7所示的转矩-转速曲线，曲线斜率即为粘滞摩擦因数。粘滞摩擦因数与转速关系曲线如图8所示。

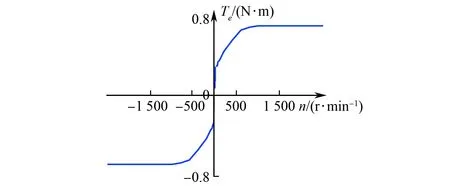
图7 转矩-转速曲线

图8 粘滞摩擦因数-转速曲线

从图7和图8可明显看出粘滞摩擦因数随转速不同而变化，转速越大粘滞摩擦因数越小。试验辨识的粘滞摩擦因数为平均值，与给定正弦转速的幅值有关。从图8可看出1 500 r·min-1的粘滞摩擦因数平均值比500 r·min-1的粘滞摩擦因数平均值小，验证了图6的粘滞摩擦因数辨识结果比图5辨识值小。

5 结 语

大摩擦因数的伺服系统参数辨识结果不准确，转速跟踪误差较大。本文设计了一种同时辨识粘滞摩擦因数、转动惯量和负载转矩的自适应反步转速控制器，有效减小了转速跟踪误差。该方法结构简单，易于实现。试验结果表明系统的参数辨识值准确稳定、1 s以内即可收敛至真实值，辨识速度快、精度高，具有良好的转速跟踪性能和参数鲁棒性。

[1] 王江,王静,费向阳.永磁同步电动机的非线性PI速度控制[J].中国电机工程学报,2005,25(7): 125-130.

[2] 王瑞萍,皮佑国.基于分数阶PI速度控制器的永磁同步电动机控制[J].电工技术学报,2012,27(11): 69-75.

[3] 黄庆,黄守道,冯垚径,等.基于变结构自抗扰的永磁电动机速度控制系统[J].电工技术学报,2015,30(20): 31-39.

[4] 张晓光,赵克,孙力,等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报,2011,31(24): 77-82.

[5] 刘栋良,崔言飞,赵晓丹,等.基于反推控制的永磁同步电动机速度的模糊控制[J].电工技术学报,2014,29(11): 38-44.

[6] LI S, GU H. Fuzzy adaptive internal model control schemes for PMSM speed-regulation system[J].IEEE Transactions on Industrial Informatics,2012,8(4): 767-779.

[7] 王同旭,马鸿雁,聂沐晗.电梯用永磁同步电机BP神经网络PID调速控制方法的研究[J].电工技术学报,2015,30(S1): 43-47.

[8] 王家军,赵光宙,齐冬莲.反推式控制在永磁同步电动机速度跟踪控制中的应用[J].中国电机工程学报,2004,24(8): 95-98.

[9] 刘栋良,郑谢辉,崔丽丽.无速度传感器永磁同步电机反推控制[J].电工技术学报,2011,26(9): 67-72.

[10] 付培华,陈振,丛炳龙,等.基于反步自适应滑模控制的永磁同步电机位置伺服系统[J].电工技术学报,2013,28(9): 288-293,301.

[11] 徐艳平,雷亚洲,马灵芝,等.基于反推控制的永磁同步电机新型直接转矩控制方法[J].电工技术学报,2015,30(10): 83-89.

[12] TING C, CHANG Y, SHI B, et al. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive[J].IET Electr Power Appl,2015,9(3): 265-279.

[13] 刘栋良,王家军,崔丽丽.永磁同步电机参数自适应调速控制[J].电工技术学报,2011,26(8): 159-165.

[14] 郭阎彦,刘锐,史婷娜,等.基于反推自适应控制的永磁同步电机摩擦力矩补偿策略[J].中国电机工程学报,2013,33(33): 76-84.

[15] ZHOU J, WANG Y. Adaptive backstepping speed controller design for a permanent magnet synchronousmotor[J].IEE Proceedings-Electric Power Applications,2002,149(2): 165-172.

[16] 范仁凯.直接驱动永磁同步电机的转速跟踪控制[D].南京: 南京航空航天大学,2013.

AdaptiveBacksteppingControlofPermanentMagnetServoSystemwithLargeViscousCoefficient*

WUJing,ZHUXiaoyong,ZUOYuefei,ZHANGChao,QUANLi

(School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China)

For permanent magnet servo system with large coefficient of viscous friction, traditional adaptive backstepping control could result in fluctuated and unstable identification results and poor performance of speed tracking. Adaptive backstepping controller identifying viscous friction coefficient was proposed, which was used to estimate the inertia, load torque and viscous friction coefficient simultaneously, improved parameter identification accuracy. The method proposed in this paper had merits of simple structure and usability. The validity and accuracy were verified by experiments based on the platform using dSPACE DS1103 system.

permanentmagnetsynchronousmotor(PMSM);viscousfrictioncoefficient;adaptivebacksteppingcontrol;inertia

国家自然科学基金项目(51477069)；国家自然科学基金项目(51377073)

吴 晶(1992—)，女，硕士研究生，研究方向为永磁同步电机的参数辨识。

朱孝勇(1975—)，男，博士生导师，教授，研究方向为电动汽车驱动控制技术、新型电机设计与控制等。

TM 301.2

A

1673-6540(2017)12- 0030- 06

2017 -02 -24