基于改进内模控制的永磁同步电机电流环设计*

张 涛, 余海涛

(东南大学 电气工程学院，江苏 南京 210096)

基于改进内模控制的永磁同步电机电流环设计*

张 涛, 余海涛

(东南大学 电气工程学院，江苏 南京 210096)

永磁同步电机(PMSM)作为一种高阶非线性系统，由于参数摄动和外部干扰的原因，传统内模控制器不能保证其精确的控制要求。在传统内模控制的基础上，设计了一种基于指数收敛的误差干扰观测器。在解耦和反电动势补偿情况下，建立内模控制器，然后由内模控制器的输出和反馈电流，构造误差干扰观测器的状态方程，输出误差补偿信号，补偿电机运行过程中参数变动和干扰因素，实现PMSM的高精度控制。建立MATLAB/Simulink仿真模型，仿真中人为增加不确定量和扰动。仿真结果表明，在存在不确定信号和负载扰动时，采用改进的内模控制可以实现电流补偿，降低电流纹波，减小电流稳态误差，同时提高转速响应速度，降低扰动误差。

永磁同步电机;内模控制;干扰观测器;误差补偿

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有体积小、起动力矩大、功率因数高、效率高等特点，在调速系统中得到广泛应用。PMSM常用的调速方式有：恒压频比控制、矢量控制[1]、直接转矩控制[2]等。相比较其他控制方式，矢量控制可近似解耦交轴电流iq和直轴电流id，从而获得像他励直流电机相同的性能。由于PMSM的强耦合非线性特性，采用传统PI控制很难满足控制系统高性能的要求，因此需要采取高效的、先进的控制策略，设计出一种响应速度快、稳态误差小、鲁棒性高的控制器。

在PMSM运行的过程中，存在参数摄动、负载扰动和非线性未建模因素等干扰，严重影响控制器的性能。新型控制理论的应用使得控制性能不断改善，其中滑模变结构控制[3]、自适应控制[4]、参数在线识别[5]和内模控制[6]等应用最为广泛。内模控制具有良好的动态性能、稳定性和鲁棒性。在内模控制器设计中，被控对象的数学模型的准确性是整个设计的核心。由于PMSM的非线性和参数不确定性，不可能得到其精确的数学模型，很多学者提出了改进算法以提高内模控制器的性能。文献[7]将自适应技术应用在内模控制中，提高了系统的鲁棒性，但却降低了系统的响应速度。文献[8]利用神经网络的在线识别特性、非线性映射能力和较强的自学习能力，提出了神经网络内模控制器，然而神经内模的逆识别控制器设计复杂，限制了其工业应用。周华伟等人[9]提出的基于内模的滑模控制器，将内模控制和滑模控制结合，其中内模控制保证系统动态响应，滑模控制保证鲁棒性，提高了系统的抗干扰能力。文献[10]提出了一种基于内模的观测器，将实际电流与内模电流的误差经过观测器，补偿电流环误差，获得了良好的控制性能。

本文基于上述文献，提出了一种新的内模控制，在内模控制的基础上增加一种基于指数收敛的误差干扰观测器，将实际值与内模控制器估计值的误差量补偿在电流环控制器中，在保证系统响应速度的同时，提高了系统的鲁棒性。

1 PMSM的数学模型

dq0坐标系下，PMSM的基本电压方程表示为

ud=Rsid+pψd-ωψq(1)

uq=Rsiq+pψq-ωψd(2)

定子磁链方程表示为

式中：ud、uq——定子电压的直、交轴分量；

Rs——定子绕组电阻；

p——微分算子；

ω——电机电角速度；

ψd、ψq——直、交轴磁链；

Ld、Lq——直、交轴电感；

id、iq——定子电流的直、交轴分量；

ψf——永磁磁链。

将式(3)和式(4)代入式(1)和式(2)，导出电流环数学模型为

(5)

电磁转矩方程为

(6)

式中：TL——负载转矩；

J——转动惯量；

B——转矩摩擦系数；

ωm——转子机械角速度(ω=pωm)。

id，iq解耦后，其表达式为

(7)

经过拉普拉斯变换后可以表示为

Y(s)=G(s)U(s)(8)

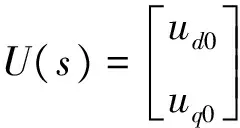
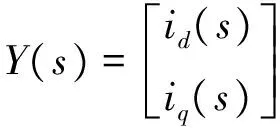
由此可见，电流环系统经过解耦后为一阶系统。

当实际系统发生参数摄动和干扰时，电流模型表达式可以写为

(9)

2.社会主义建设初期与党的群众史观。新中国成立后，中国共产党所处的地位、所面临的环境和所承担的责任都随着党的任务的转变而发生了重大变化。毛泽东作为党的领袖和代表，在执政过程中，关于群众问题，又提出了新的主张，进一步丰富和发展了马克思主义群众史观的内容。

式中：dq、dd——电流模型中的不确定量；

ΔLq、ΔLd、ΔRs、Δψf——实际值与建模值的偏差；

εq、εd——未建模量和不可测干扰。

2 电流控制器设计

在PMSM的矢量控制策略中，采用转速外环、电流内环的双环控制策略。转速环采用PI控制。

2. 1 内模控制器设计

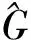
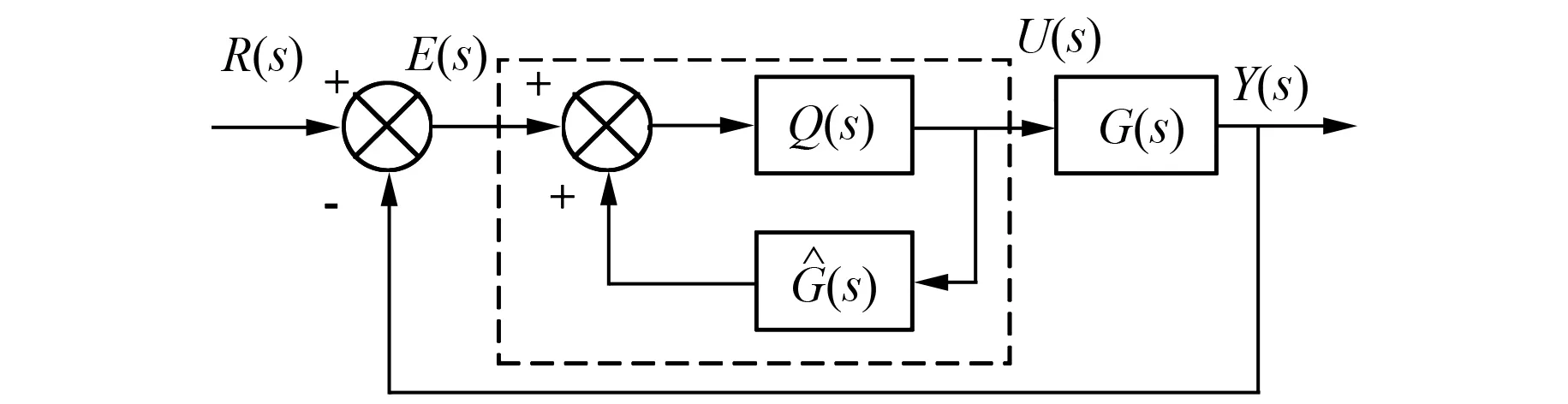
图1 IMC原理结构图

图1中虚线为IMC控制器部分，其传递函数采用C(s)表示，则：

(11)

由于被控对象是一阶系统，根据内模控制原理，取

式中：f(s)——滤波器；

λ——滤波器的时间常数。

(13)

IMC控制类似于PI控制器，但只有一个控制参数λ，控制简单。采用最大灵敏度内模整定方法对参数λ进行整定[11]：

(14)

其中：Ms的值为1.2～2，对应的控制系统的幅值裕度和相角裕度，分别为6.0～2.0和49.2～29.0。

基于IMC控制的电流控制器如图2所示。

图2 基于IMC的电流控制原理图

2. 2 指数收敛干扰观测器设计

本文针对电流环特点，提出一种基于指数收敛的干扰观测方法。采用估计值输出与实际值输出的误差对估计值进行修正。将式(5)d-q电流模型采用状态方程表示，则q轴电流状态方程为

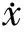
其中：x=iq；a=-Rs/Lq；b=1/Lq；u=uq-(ωLqid+ωψf)；d=dq/Lq。

采用指数收敛的干扰观测器设计为

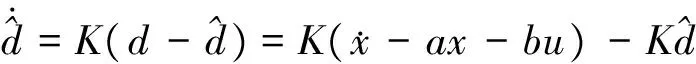
(16)

定义辅助变量z：

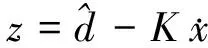
(17)

则：

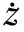
将式(16)代入式(18)得

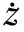
从而可得基于指数收敛的误差干扰观测器为

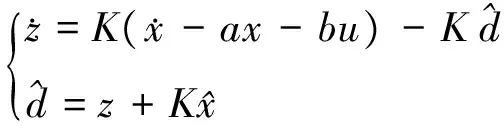
(20)

则：

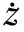
取观测器观测误差为

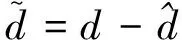
(22)

(23)

将式(21)代入式(23)得

从而得到观测器的观测误差方程为

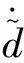
即：

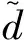
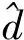
同理可得d轴电流干扰观测器。

图3所示是带有干扰观测器的改进内模控制(Improved Internal Model Control，IIMC)电流环原理图。

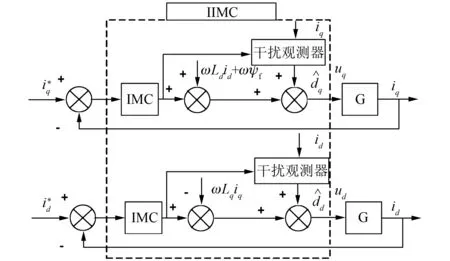
图3 基于IIMC的电流环控制原理图

图4 基于IIMC控制的PMSM矢量控制结构框图

3 仿真及结果

基于上述理论分析，搭建MATLAB仿真模型，如图4所示是基于IIMC的PMSM控制结构框图。PMSM的参数如表1所示。

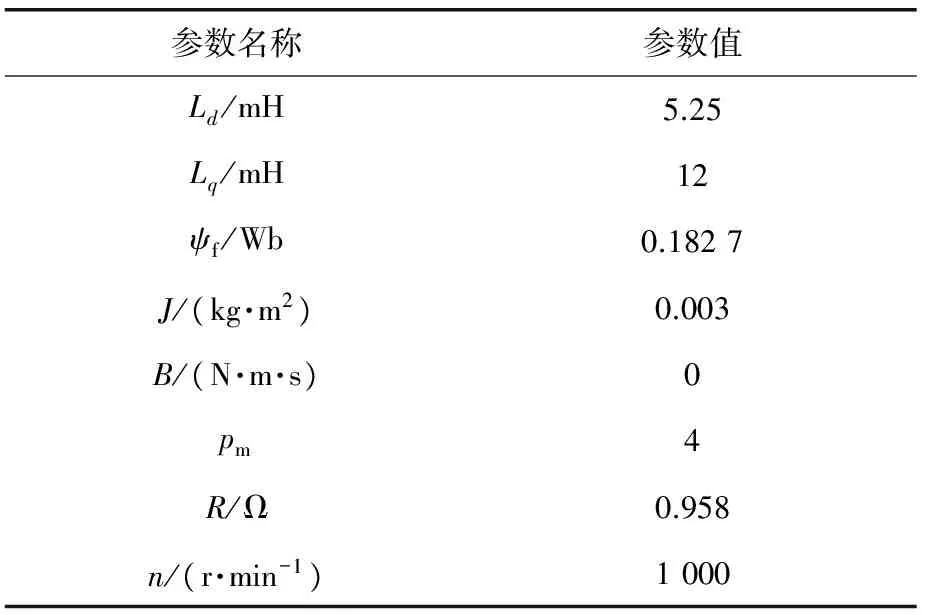
表1 PMSM电机的参数

仿真时间T=0.4 s，负载转矩在0.2 s时由5 N·m变为10 N·m；转速在0.3 s时由1 000 r/min突变为1 500 r/min。同时加入不确定量为ΔRs=0.1δRs，ΔLq=0.1δLq，ΔLd=0.1δLd，Δψf=0.1δψf，εq=εd=2δ，其中δ为均值0、幅值±1的随机噪声干扰。

图5所示是采用传统IMC电流控制输出交轴电流和直轴电流波形。图6所示为采用IIMC电流控制输出交轴电流和直轴电流波形。图5和图6中虚线框中图形为放大后波形图。

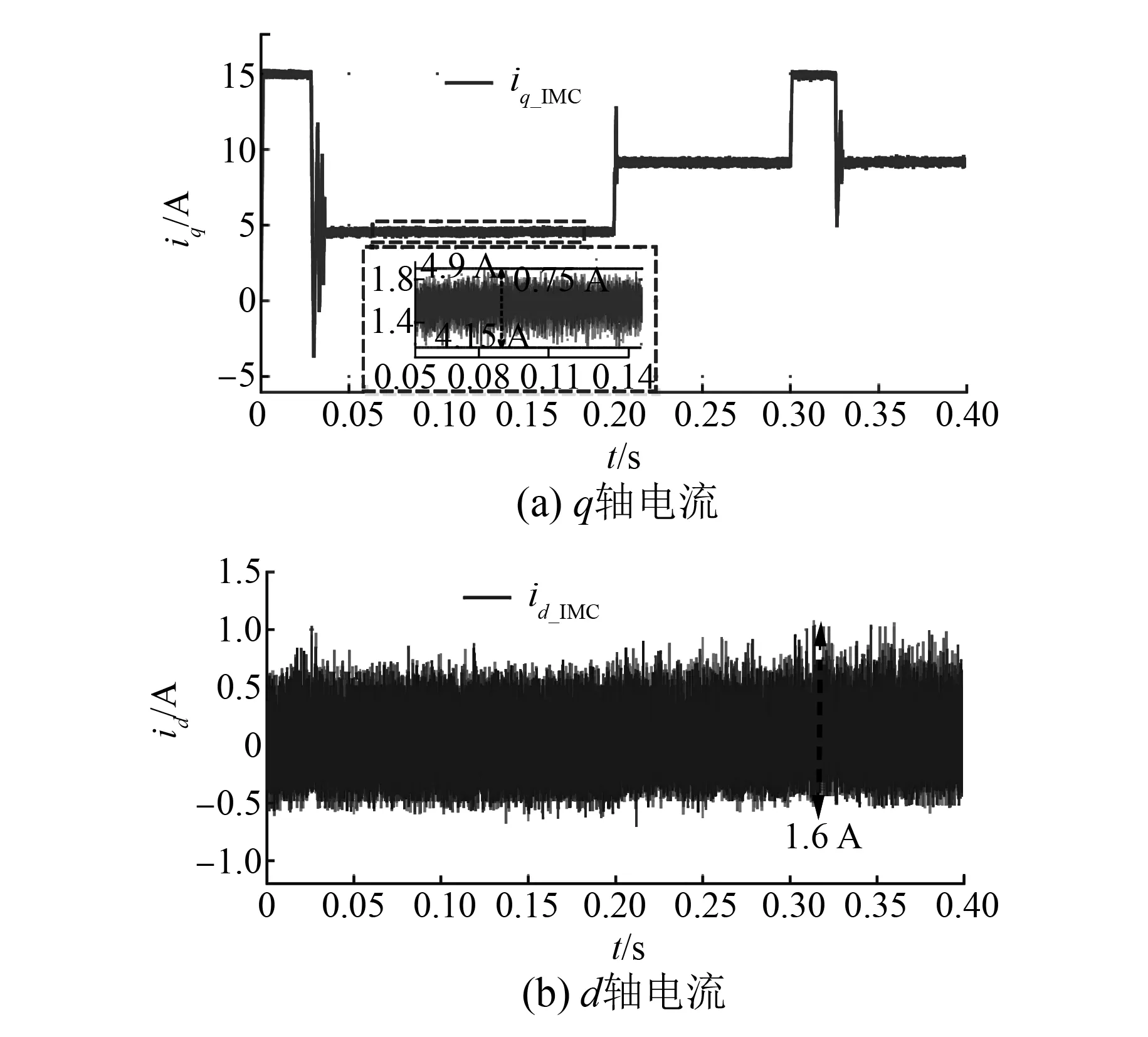
图5 采用传统IMC控制电流波形

图6 采用IIMC控制电流波形

对比图5和图6，在负载突变扰动时，传统IMC控制和IIMC控制均能快速跟随负载变化。从图5(a)和图6(a)中虚线框图可以看出，采用传统IMC控制，额定转速下交轴电流脉动约为0.75 A，纹波为16.7%，直轴电流脉动为1.6 A。采用IIMC控制时，电流纹波明显减小，额定转速下，交轴电流脉动仅为0.1 A，纹波降低为2.2%，直轴电流脉动也减小为0.1 A。从而验证了内模控制可以实现电流的快速跟踪，在IMC控制的基础上增加指数收敛误差干扰观测器，可以实现电流补偿，抑制电流纹波。

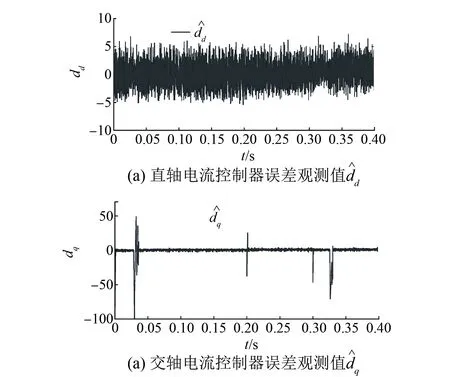
图7 误差观测器观测值

图8 采用IIMC电流控制转子转速波形

4 结 语

本文针对PMSM系统，在IMC电流环的基础上，结合基于指数收敛的误差干扰观测器，提出了一种新的电流IMC控制器。该控制器通过补偿传统IMC控制器输出的控制量，提高了控制器的控制性能。在MATLAB/Simulink仿真环境下对该系统进行了干扰噪声下的仿真，仿真结果证明采用IIMC控制器可以实现电流补偿，抑制电流纹波，同时提高转速的响应时间，降低转速稳态误差。验证了理论分析的有效性。

[1] 袁登科,徐延东,李秀涛.永磁同步电动机变频调速系统及其应用[M].北京: 机械工业出版社,2015.

[2] 立正,胡育文.永磁同步电机直接转矩控制转矩调节器设计[J].中国电机工程学报,2011,31(9): 76-81.

[3] 李政,胡广大,崔家瑞.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3): 431-437.

[4] 王庆龙,张兴,张崇巍.永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J].中国电机工程学报,2014,34(6): 897-902.

[5] CHANG S H, CHEN P Y, TING Y H, et al. Robust current control-based sliding mode control with simple uncertainties estimation in permanent magnet synchronous motor drive systems[J].Electric Power Applications,IET,2010,4(6): 41-50.

[6] LIU G H, CHEN L L, ZHAO W X, et al. Internal model control of permanent magnet synchronous motor using support vector machine generalized inverse[J].IEEE Transactions on Industrial Informatics,2013,9(2): 890-898.

[7] 任荣杰,高强,王卫.永磁同步压缩机自适应内模控制方法研究[J].伺服控制,2009(2): 27-29.

[8] 邵可可,郭兴众,陆华才.永磁直线同步电机神经网络的内模控制[J].长春工业大学学报(自然科学版),2012,33(4): 416-419.

[9] 周华伟,温旭辉,赵峰,等.基于内模的永磁同步电机滑模电流解耦控制[J].中国电机工程学报,2012,32(15): 91-99.

[10] 黄宴委,熊少华.基于内模控制的永磁同步电机电流环观测器设计[J].中国电机工程学报,2016,36(11): 3070-3075.

[11] ZHAO Z C, LIU Z Y, ZHANG J G. IMC-PID tuning method based on sensitivity specification for process with time-delay[J].Journal of Central South University,2011,18(40): 1153-1160.

DesignofImprovedInternalModelControlforCurrentLoopofPermanentMagnetSynchronousMotor*

ZHANGTao,YUHaihao

(College of Electrical Engineering, Southeast University, Nanjing 210096, China)

Permanent magnet synchronous motor (PMSM) was considered as a high order nonlinear system due to the parameter uncertainties and external disturbances. Superior control performance could not be guaranteed by using internal model control (IMC). An exponential convergence control-based observer was derived to estimate uncertainties. An internal model was set up under the condition that coupling term and back electromotive force were compensated completely. Then, a state-space model for observer was constructed based on output term of IMC and feedback current. Finally the prediction error was obtained to estimate uncertainties. The system was simulated by MATLAB / Simulink. Simulation results showed that by using improved internal model control (IIMC), the disturbance observer could realize the current compensation, suppress the current ripple, reduce the steady-state error, and improve the response of speed, reduce the fluctuation of speed error under load disturbance.

permanentmagnetsynchronousmotor(PMSM);internalmodelcontrol(IMC);disturbanceobserver;errorcompensation

国家自然科学基金项目(41576096)

张 涛(1990—)，女，硕士研究生，研究方向为直线电机伺服振动控制。

余海涛(1965—)，男，教授，博士生导师，研究方向为直线电机、驱动控制、新能源发电。

TM 301.2

A

1673-6540(2017)12- 0001- 05

2017 -03 -13