控制系统延迟对轴扭振的影响
程天威, 王 爽, 杨 影
(上海大学 机电工程与自动化学院,上海 200072)
控制系统延迟对轴扭振的影响
程天威, 王 爽, 杨 影
(上海大学 机电工程与自动化学院,上海 200072)
控制系统中的轴扭振会引起系统控制量的振荡,加大机械传动装置磨损,甚至会导致传动轴断裂。在工业应用中,多采用陷波滤波器抑制轴扭振,而陷波频率的选取通常未考虑控制系统延迟因素。基于电机角速度增量、轴转矩增量和电机电磁转矩增量的相位图,分析了控制系统延迟对轴扭振频率的影响。仿真结果对分析结论给予了验证。
控制系统;轴扭振;陷波频率;延迟
0 引 言
目前电机传动系统多为两质量或三质量系统,主要包括控制器、驱动器、电动机和机械传动装置等。其中常用到的传动轴、变速器和联轴器等机械传动装置不是理想刚体。随着应用工况对电机传动系统动态性能的要求越来越高,系统频带逐渐增宽。当两质量机械传动装置的固有谐振频率落在系统带宽内时,系统便会产生谐振。如果此时的固有谐振频率信号没有得到有效地衰减,系统中就会出现持续的谐振现象。长时间工作在这种谐振状态,会导致系统性能恶化和零部件寿命缩短,甚至会使传动轴断裂[1]。
对速度指令加一个低通滤波器是一种避免轴扭振的方法,但这会降低伺服系统的频响带宽[2]。基于陷波滤波器的轴扭振抑制方法能够衰减指定频率的幅值而对其他频率没有影响[3-5]。在包含弹性机械传动装置的转速电流闭环系统中,将陷波滤波器串入速度控制环路中,对转速调节器输出的电流环给定信号进行陷波处理,从而抑制电机电流的振荡,进而达到抑制轴扭振的目的[6]。陷波滤波器的抑制效果主要取决于陷波频率选取。如果设计的陷波频率出现偏差,会影响轴扭振的抑制效果,严重时甚至不再适用[7]。
两质量系统中的控制环节包括转速调节器、电流调节器和测速环节等。通常分析的轴扭振频率是由两质量机械传动装置得出的,并没有考虑控制环节的影响。现代电机传动系统是数字控制系统,其以离散时间步长方式运行。离散时由存储数据产生的采样-保持延迟、由执行控制律需要时间产生的计算延迟和由位置估计速度产生的速度估计延迟,都可能会对轴扭振产生影响,其中延迟的作用可以用相位滞后量来表示[8]。
本文基于电磁转矩增量相对于角速度增量的相位关系,开展了研究控制系统延迟对轴扭振的影响分析。由于电流环的采样频率相比于转速环很快,所以本文着重分析由数字控制在转速环中引入的延迟对轴扭振的影响。
1 两质量系统中的轴扭振
对两质量机械传动装置建模时,可将机械传动装置认为是一个具有机械阻尼特性的弹簧,而电机侧和负载侧可分别简化为具有一定惯量的刚体,如图1所示。

图1 两质量机械传动装置模型
其中:JM——电机侧转动惯量;
JL——负载侧转动惯量;
DS——阻尼系数;
KS——刚度系数;
Δθ——轴扭转角;
TS——轴转矩;
TM——电机电磁转矩;
TL——负载转矩;
ωM——电机角速度;
ωL——负载角速度。
由图1可得轴转矩方程和运动方程为
(1)
由于系统的阻尼系数较小,在忽略阻尼系数后,根据式(1)可得两质量机械传动装置模型结构图如图2所示,其中TD为电机动态转矩。

图2 两质量机械传动装置模型结构图
即:TM-TS=TD;TD=JMSωM
(2)
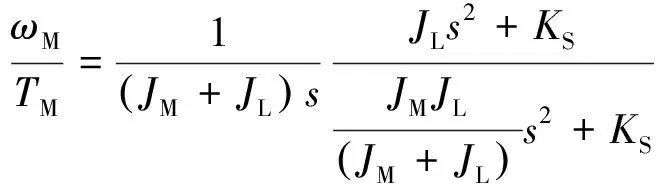
由式(3)可计算出固有谐振频率为
(4)
2 延迟对轴扭振的影响分析
将由数字控制引入的延迟等效到反馈通道上,可得延迟的传递函数为
(5)
其中τ为延迟时间。
式中:G(s)——延迟环节的传递函数;
C(s)——延迟环节的输出量;
R(s)——延迟环节的输入量。
当延迟时间很小时,常把它展开成泰勒级数,并略去高次项:
(6)
由式(6)可得含有延迟的闭环系统框图,如图3所示。其中转速环采用PI调节器,传递函数为
(7)
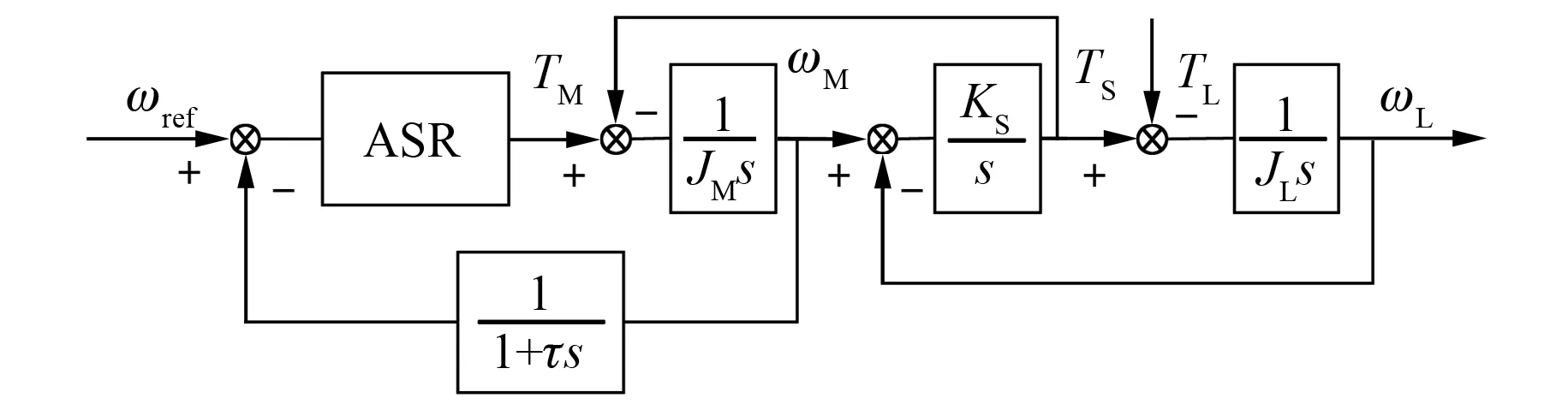
图3 含有延迟的闭环系统框图
由图3可得包含延迟的从电机电磁转矩到电机角速度的传递函数为
式中:KP——转速调节器的比例系数;
KI——转速调节器的积分系数。
用jω代替s,可得延迟的传递函数为
(9)
转速调节器ASR的输入是转速偏差,在用小信号分析扭振时为-ΔωM。由图3可知,此时ΔTM相对于-ΔωM的总相位滞后角为转速调节器本身引入的相位滞后角与延迟引入的相位滞后角之和:
α=θASR+θDelay(10)
其中:转速调节器本身引入的相位滞后角与延迟引入的相位滞后角分别为
(11)
θDelay=arctan(ωτ)(12)
分析式(11)与式(12)可知0<θASR<90°、0<θDelay<90°,进而可知0<α<180°。
为便于分析延迟对轴扭振的影响,引入延迟系数D。延迟系数D与延迟时间τ和固有谐振频率f0的关系如下:
(13)
将式(13)代入式(12)可得
(14)
分析式(14)可知,轴扭振频率f和固有谐振频率f0是一个数量级的,延迟的引入使得总相位滞后角α受延迟系数D的影响很大。接下来分析总相位滞后角α对轴扭振的影响。
利用机电模拟法,将刚度系数KS等效成电感,电机侧转动惯量JM和负载侧转动惯量JL等效成电容,阻尼系数DS等效成电阻,电机角速度ωM和负载角速度ωL等效成电压,电机电磁转矩TM、负载转矩TL和轴转矩TS等效成电流源,如图4所示。

图4 等效电路图
轴扭振发生后,轴转矩的振荡导致电机角速度振荡,然后通过电机电势振荡或转速电流闭环系统的控制,造成电机电流和电磁转矩振荡。
将式(2)改写为增量方程,并用jω代替s,可得到两质量机械传动装置的频率特性为
(15)
通常大型设备运行时负载转矩基本不变或变化慢,在分析轴扭振时可认为ΔTL=0。由图4可知,在ΔTL=0的条件下,相当于负载电流源支路开路,再用jω代替s,可得
(16)
在轴扭振发生时,两质量机械传动装置处于谐振状态,此时电机角速度增量ΔωM、电机电磁转矩增量ΔTM和轴转矩增量ΔTS,都是以谐振频率进行振荡的正弦波。由式(16)可知,ΔωM的幅值与ΔTS的幅值成比例,相位超前90°,而由式(15)可知,ΔTM的幅值与ΔTS的幅值成比例,所以ΔTM的幅值与ΔωM的幅值也成比例。在闭环控制系统中,控制系统延迟和转速调节器本身会引入一定的相位滞后角,使ΔTM相位滞后于-ΔωM相位。
为了便于分析,这里将ΔTM进行分解,可得
(17)
把式(17)代入式(15)中,化简可得
(18)
由式(18)可知两质量机械传动装置的谐振频率为
(19)
由式(19)可知系数λM.1使两质量机械传动装置的谐振频率fres偏离固有谐振频率f0,有以下3种情况:
(1) 若系数λM.1>0,则fres>f0。
(2) 若系数λM.1=0,则fres=f0。
(3) 若系数λM.1<0,则fres 由式(15)和式(16)可得ΔTM、ΔωM和ΔTS间的相位图,如图5所示。由图5中ΔTM.2与ΔωM相位关系可知有以下3种情况: 图5 相位图 (1) 当ΔTM.2与ΔωM方向相反时,ΔωM的振荡幅度会被ΔTM.2衰减,系统呈现衰减振荡。 (2) 当ΔTM.2与ΔωM方向相同时,ΔωM的振荡幅度会被ΔTM.2增强,系统呈现发散振荡。 (3) 当ΔTM.2等于零时,ΔωM的振荡幅度不会被ΔTM.2影响,系统呈现等幅振荡。 由0<α<180°可知ΔTM位于第3象限或第2象限。由图5可得当ΔTM位于第3象限,有λM.1>0和λM.2>0。由系数λM.1>0可知fres>f0。由式(17)可知ΔTM.2的值取决于λM.2,当系数λM.2>0时,ΔTM.2与ΔωM方向相反,系统引入阻尼,ΔωM呈现衰减振荡。此时α角越小,阻尼越强,对系统振荡幅度衰减得越厉害。 仿真分析选用的参数如下:电机侧惯量为1.03 kg·cm2;负载侧惯量为0.011 kg·m2;刚度系数为349.06 N·m/rad;阻尼系数为0;负载转矩为0,速度指令为阶跃信号,在0.01 s给定300 rad/s。 由式(3)可得两质量机械传动装置Bode图,如图6所示。其中抗谐振频率和固有谐振频率分别为28.4 Hz和294 Hz。通过式(4)计算出的固有谐振频率也为294 Hz,与图6的结果一致。 图6 两质量机械传动装置Bode图 下面分别对延迟系数D取不同的值,得到式(8)的Bode图,如图7所示。 图7 延迟Bode图 为了便于分析延迟对轴扭振的影响,将图7中的数据制成表,如表1所示。 表1 延迟与轴扭振的关系 从表1可知延迟的引入使得轴扭振频率偏移固有谐振频率的幅度很明显。此时不可忽略延迟对轴扭振的影响。 图8 未引入延迟仿真结果 为进一步分析延迟对轴扭振的影响,给出电机电磁转矩、轴转矩和电机角速度的仿真结果,如图8和图9所示。其中图8为未引入延迟时的情况,图9为引入不同的延迟系数时的情况。 图9 引入延迟仿真结果 在转速上升阶段由于转速调节器饱和,电机电磁转矩为恒定值,即电机电磁转矩增量为零,可得λM.1=0和λM.2=0,所以此时轴转矩应以固有谐振频率进行等幅振荡。由图8可知,在转速上升阶段轴转矩的确呈现等幅振荡,且对其进行FFT分析得到的结果为294 Hz,与理论分析一致。 图8中转速达到给定值时,转速环会退饱和,电机电磁转矩会产生波动,此时电机电磁转矩增量不等于零,系统会引入阻尼,导致振荡呈现衰减形式。图9中转速上升阶段的退饱和因为延迟的引入而会有段滞后。 分析延迟对轴扭振的影响时,对图9中D=2时转速稳定阶段的轴转矩进行FFT分析,得到的结果为312 Hz。 由图5分析可知,ΔTM的位置可由ΔTM滞后-ΔωM的角度推得。通过计算可得,当D=0.5时,滞后角约等于75.3°;当D=2时,滞后角约等于85.7°。 当D=0.5和D=2时,ΔTM都位于图5中的第3象限,所以有系数λM.1>0和λM.2>0。由式(19)可知,因为系数λM.1>0,所以此时轴扭振频率比固有谐振频率大,而由系数λM.2>0可知此时系统引入阻尼,对振荡的幅值起衰减作用,振荡呈现衰减形式。 由于D=0.5时的α角比D=2时来得小,所以在D=2时振荡更加剧烈。结合图9的结果可验证上述分析。 本文通过两质量机械传动装置的轴转矩方程和运动方程得到系统结构图和等值电路图,进一步分析得到电机角速度增量、轴转矩增量和电机电磁转矩增量的相位图,然后从电机电磁转矩增量相对于电机角速度增量相位滞后的角度分析控制系统延迟对轴扭振的影响。最后利用仿真软件MATLAB进行Bode图分析及仿真验证。理论分析和仿真结果表明延迟会使轴扭振的频率产生偏移并且会对振荡的幅值产生影响。 [1] 蔡昆,马小亮.电气传动中的扭振现象及其抑制[J].电气自动化,2000,41(5): 19-21. [2]MURPHYBR,WATANABLEI.Digitalshapingfiltersforreducingmachinevibration[J].RoboticaandAutomation,IEEETransactionson,1992,8(2): 285-289. [3]ELLISG,LORENZRD.Resonantloadcontrolmethodsforindustrialservodrives[C]∥ 2000IndustryApplicationsConference,2000: 1438-1445. [4]HSUWC,LAICL,HSUPL.Anoveldesignforvibrationsuppressionforlightly-dampedservocontrolsystem[C]∥Proceedingsof2011 8thAsianControlConference,2011: 251-256. [5] 夏超,那学智,柴晓慧,等.伺服系统机械谐振机理与抑制方法分析[J].导航定位与授时,2016,3(1): 29-35. [6]SHENGMY,SHIHCW.Thedetectionofresonancefrequencyinmotioncontrolsystems[J].IEEETransactionsonIndustryApplications,2014,50(5): 3423-3427. [7] 王建敏,吴云洁,刘佑民,等.基于数字滤波器的伺服系统谐振抑制方法[J].北京航空航天大学学报,2015,41(3): 485-491. [8]ELLISG.控制系统设计指南[M].汤晓君,译.北京: 电子工业出版社,2006. InfluenceofControlSystemDelayonShaftTorsionalVibration CHENGTianwei,WANGShuang,YANGYing (College of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China) The shaft torsional vibration of control system would cause the oscillation of system control quantity, which would increase mechanical transmission gear wears, and even led to the shaft fracture. The shaft torsional vibration could usually be suppressed by using notch filter on industrial application, but the selection of notch frequency was not considering the factor of control system delay. The influence of control system delay on shaft torsional vibration was analyzed by using the phase diagram of angular velocity increment, shaft torque increment and motor torque increment. Simulation results validated the analytical conclusions. controlsystem;shafttorsionalvibration;notchfrequency;delay 程天威(1991—),男,硕士研究生,研究方向为电力电子与电力传动。 王 爽(1977—),男,博士,研究方向为电力电子与电机驱动控制。 TM 301.2 A 1673-6540(2017)12- 0025- 05 2016 -12 -13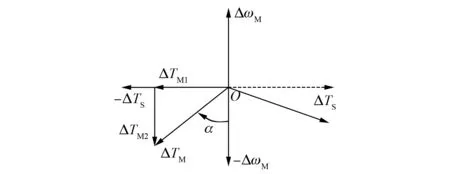
3 仿真分析
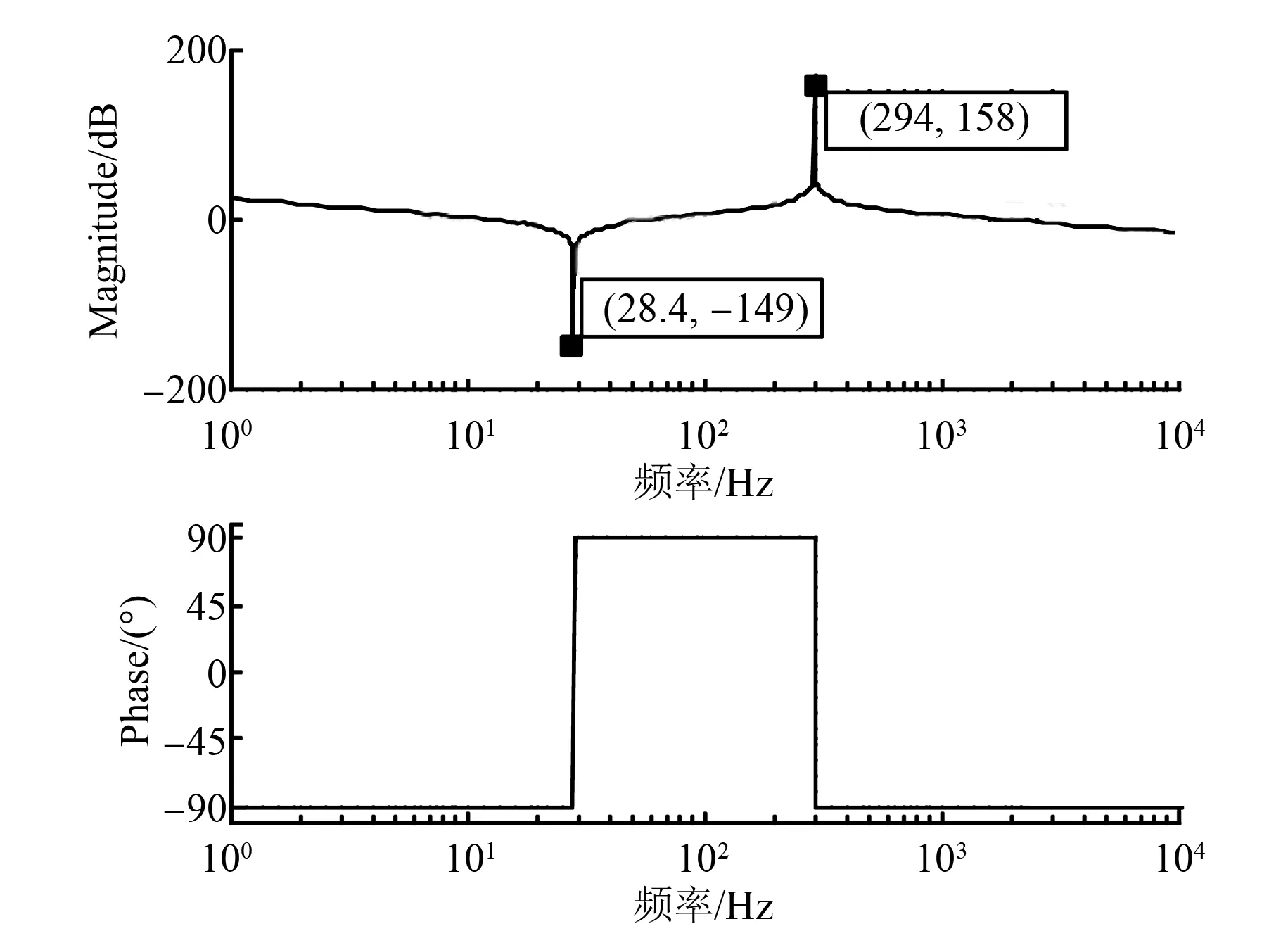
4 结 语

