基于随机合作博弈的水电工程EPC项目风险分担研究

王 娜,候嫚嫚

(河海大学 工程管理研究所，江苏 南京 211100)

基于随机合作博弈的水电工程EPC项目风险分担研究

王 娜,候嫚嫚

(河海大学 工程管理研究所，江苏 南京 211100)

水电工程EPC项目具有工程大型性、施工复杂性、影响全局性等特点，直接决定了参与方在项目实施过程中必然面临众多风险。合理的风险分担不仅能满足各参与方效用最大，还可提高项目的风险管理水平。鉴于此，应用随机合作博弈理论，构建参与方之间的最优合作博弈模型，在基于参与方风险偏好的基础上，实现双方之间的风险转移。结果分析表明，该模型既可确定各参与方最优风险分担的比例，又可使风险转移后的项目总风险降低，实现了合作效率。

水电工程；EPC项目；风险分担；随机合作博弈

我国现行《建筑法》在第二十四条规定：“提倡对建筑工程实行总承包，禁止将建筑工程肢解发包。建筑工程的发包单位可以将建筑工程的勘察、设计、施工、设备采购一并发包给一个工程总承包单位，也可以将建筑工程勘察、设计、施工、设备采购的一项或者多项发包给一个工程总承包单位。”这一规定，在法律层面为项目总承包模式(engineering procurement construction,EPC)在我国建筑市场的推行提供了具体法律依据。但水电工程EPC项目往往具有工程情况复杂、操作周期长、投资规模大、施工作业环境恶劣的特点，使得项目在执行过程中潜在风险增加[1-2]。显然，风险的合理分配成为项目各参与方在签订合约时关注的重点和焦点，而合理的风险分担方式不仅能节约投资费用和资本成本，还能改善项目的收益，提高项目组的管理水平，获取较高的项目质量[3-4]。大量事实表明，水电项目在合约谈判过程中，花费在风险分担谈判上的成本和精力占很大部分，这大大增加了水电项目各参与方的参与成本。因此如何设计合理的风险分担方案，既满足各参与方个体理性又满足集体理性，成为水电工程EPC项目研究的关键问题[5]。

目前这方面研究主要集中在管理模式和风险评估两方面。①管理模式方面，如吴云良等[6-8]针对水电工程EPC项目的管理模式做了相关研究；王腾飞等[9]在国际工程的背景下，基于伙伴关系构建水电EPC项目的设计管理模型，通过实证分析指出伙伴关系可以改善项目绩效；刘纳兵等[10]针对水电工程EPC项目设计、采购和施工阶段中的关键问题，基于系统论的观点构建了总承包商设计管理的集成模式，并提出有效的设计管理方法；陶自成等[11]则研究了以施工为主导的企业如何在国际EPC水电工程中具有较大的竞争实力，并提出一系列设计管理思路。②风险评估方面，如张建成等[12]从总承包商的视角，利用全面风险管理理论分析水电 EPC 项目的总承包商风险，并提出全面风险集成模式；李超娟[13]综合应用熵权、灰色系统理论及模糊综合评价方法构建中小型水电工程EPC项目的风险评价模型；刘东海等[14]针对水电工程EPC项目的自身特点，运用熵权的风险综合评价方法，对风险因素进行排序，从而为总承包商采取相应的风险措施提供依据；陈志鼎等[15]基于水电工程EPC项目中风险发生的影响程度和发生概率，构建了水电工程 EPC 项目采购风险评价体系；李卉[16]在前人研究的基础上，充分考虑专家判断的模糊性，引入三角模糊数对传统的模糊层次分析法进行改进；赵美玲等[17]利用TOC(约束理论)和SPA(集对分析理论)，提出关于水电工程EPC 工作流程的内部风险预报和外部管理程序相结合的风险管理动态循环模型，实现全方位、全系统的优化管理。

上述研究虽然是通过定性或定量的方法构建风险分担模型，但大多数研究局限于风险评价方法或风险因素的分析上，却鲜有研究考虑到工程项目风险因素的不确定性和风险在各参与方之间的转移而影响合作的实现问题。因此，笔者在上述研究的基础上，充分考虑参与方的风险偏好并研究风险在彼此之间转移问题，构建基于随机合作博弈的政府部门和总承包方之间最优风险分担决策模型。结果表明，最优随机合作博弈模型不仅能确定各参与方的风险最优分配比例，还能使风险转移后的总项目风险降低，提高了水电工程EPC项目各参与方间的合作效率。

1 随机合作博弈模型

合作博弈理论主要研究当一部分人达成联盟和在他人联盟决策的影响下，各参与方之间的收益分配问题，主要涉及联盟的结构和联盟之间的收益分配比例的确定。由于参与方是否联盟是一个随机事件，联盟之后的收益分配又是一个随机比例，属于多种随机事件的结合。对此早在1973年，CHARNES等[18]首次研究了含有随机特征函数的合作博弈问题，随后SUIJS等[19]在前人研究的基础上对模型进行了改进，假设各参与方属于不同的风险偏好类型，而不同的风险偏好态度会导致不同的联盟收益。由于水电工程EPC项目中，系统风险具有很强的不确定性，很可能造成各参与方的收益随机性，用随机合作博弈解决水电工程EPC项目中的收益分配问题具有先天优势。

假设2若{≻i}i∈N表示参与各方的偏好关系集，则每一种风险的收益偏好可假定为A≻iB，表示相对于水电工程EPC项目系统风险B，参与者更偏好于A。若存在效用函数ui∶R→R，使得A≻iB当且仅当E(ui(A))≥E(ui(B))，则称参与方i具有冯·纽曼-摩根斯坦(VonNeumann-Morgenstern)偏好。

2 随机合作博弈的Shapley值

假设水电工程EPC项目中，各参与方的风险偏好水平确定风险行为，从风险偏好考虑，风险的态度分为风险喜好、风险中性和风险厌恶3种类型，采用Arrow-Pratt绝对风险规避度量ρ(ρ>0)定义风险偏好程度，其效用函数满足u=e(-ρiy)，其中ρi为参与方i的绝对风险规避系数，ρi越大表示参与方i风险厌恶的程度越大，各参与方越保守。

各参与方在假定风险偏好条件下也满足Shapley值。该值要求水电工程EPC项目各参与方在最大可能保证集体理性的基础上，满足各参与方的个体理性行为，以确保风险分担存在最优解。因而，在水电工程EPC项目系统风险利益不确定的前提下，先要构建随机合作博弈的Shapley值模型。

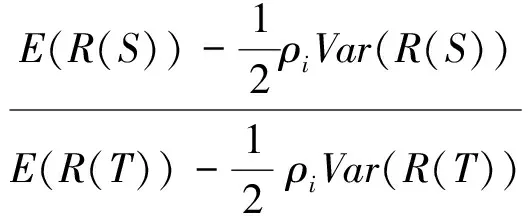
(1)

由此确定水电工程EPC项目随机合作博弈的Shapley值为:

(2)

根据水电工程EPC项目收益分配的随机博弈模型，项目风险分担比例的确定是一个多次讨价还价谈判的过程，在满足各参与方效用水平的基础上，为能够实现水电工程EPC项目的效益最大化，笔者分析各参与方风险偏好水平和谈判能力两个因素，用权重向量p={p1,p2,…,pn}替代平均权重(n！)-1，于是政府部门和总承包商方的Shapley值为：

y1=p1H1(R(1),R(N) )R(N)+

p2(1-H2R(2),R(N))R(N)

(3)

y2=p2H2(R(2),R(N))R(N)+

p1(1-H1R(1),R(N))R(N)

(4)

3 水电工程EPC项目最优风险分担模型构建

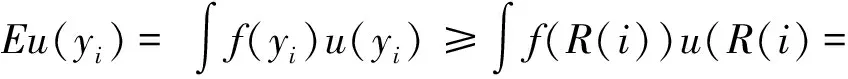
3.1 建立模型

p1+p2=1

(5)

3.2 模型求解

为了确定各参与方风险分担的最优比例，根据风险溢价函数，构建关于政府部门和总承包商间的拉格朗日方程：

L=ρ1Var(y1)/2+ρ2Var(y2)/2+γ(1-p1-p2)

(6)

根据上述方程获得水电工程EPC项目风险溢价对概率的一阶最优条件：

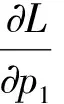
p2ρ2(1-H1)]λ2(N)-γ=0

(7)

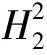
(8)

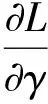
(9)

用非齐次线性方程组表示关于水电工程EPC项目风险溢价对概率的一阶最优条件为：

(10)

根据水电工程EPC项目风险溢价非齐次线性方程组特征，在满足Q=f1+f2-2f3≠0的条件下，方程有唯一解，即：

Q=f1+f2-2f3=ρ1(1-H1)2+

ρ2(1-H2)2+ρ2(1-H1)2+ρ1(1-H2)2+

(ρ1+ρ2)(2H1H2-1)

(11)

结合f1,f2,f3的公式，上式可表示为：

ρ1H1(1-H2)-ρ2H2(1-H1)]

(13)

4 结论

我国是世界上水电工程最多的国家，特别是大型水电工程，由于其会遭受到如自然灾害风险、政治风险、经济风险和技术风险等多种系统性风险，因此水电工程的设计、建设和运行会对国家、社会和生态环境产生巨大影响。只有实现水电工程EPC项目最优风险策略组合，才能使项目的潜在损失降到最低。之前关于水电工程EPC项目风险的决策工具和方法研究，虽也考虑了这些潜在风险，但我国较多水电工程EPC项目开发后，仍伴随如工期拖延、成本超支和索赔纠纷等问题。笔者基于随机合作博弈理论，充分考虑风险分担时风险在政府、总承包方之间的转移，构建了最优的风险分担比例模型，该模型有效降低了风险溢价，在满足集体理性的基础上，有效提高了水电工程EPC项目各参与方的收益，从而提高项目的风险管理水平，提升总承包项目的质量，有利于市场和企业的可持续发展。

但由于水电工程EPC项目风险分担是一个各参与方讨价还价的博弈过程，并非一次性事件，且各参与方拥有不同的风险偏好水平和效用函数，因此在水电工程EPC项目实施中，风险的分担不会像理论模型那样理想，而且最终谈判结果也需要各参与方多次、全面地沟通协商，这就使得水电工程EPC项目各个参与者在谈判前，合理确定可接受的风险程度和范围，明确阶段目标与期望效用，只有这样，水电工程EPC项目各参与方才可以通过科学合理的决策，从全局出发，对水电工程EPC项目风险进行转移、减轻和接受。

[1] 宋洪兰.面向总承包商的水电EPC项目风险分析[D].天津：天津大学,2010.

[2] 王振强,钟登华.基于模拟技术的大型水电项目财务风险分析[J].土木工程学报,2005，38(5):122-126.

[3] LAM K C, WANG D, LEE P T K, et al. Modeling risk allocation decision in construction contracts[J]. International Journal of Project Management,2007,25(5):485-493.

[4] HAMEED A, WOO S. Risk importance and allocation in the Pakistan construction industry: a contractors′ perspective[J]. Journal of Civil Engineering,2007,11(2):73-80.

[5] 蔡绍宽,李玉钦,宋洋.基于全寿命周期的水电工程项目风险管理[J].天津大学学报(社会科学版),2008,10(4):298-302.

[6] 吴云良,何武全,刘智.水电工程EPC总承包管理模式及应用[J].水资源与水工程学报,2011,22(6):155-157.

[7] 蔡绍宽.水电工程EPC总承包项目管理的理论与实践[J].天津大学学报(自然科学与工程技术版),2008,41(9):1091-1095.

[8] 曾露.基于价值管理的水电工程EPC模式项目团队管理研究[D].宜昌：三峡大学,2012.

[9] 王腾飞,唐文哲,漆大山,等.基于伙伴关系的国际EPC水电项目设计管理[J].清华大学学报(自然科学版),2016,56(4):360-364.

[10] 刘纳兵,陈晓霞.基于总承包商角度水电工程EPC项目设计管理研究[J].水电能源科学,2012,30(1):180-181.

[11] 陶自成,何彦舫.大型国际EPC水电工程项目设计管理实践探讨[J].中国水利,2015(12):29-31.

[12] 张建成,彭反霸.水电工程EPC项目总承包商全面风险管理研究[J].水电能源科学,2011,29(9):141-143.

[13] 李超娟.中小型水电工程EPC项目风险分析及对策研究[D].西安：西安建筑科技大学,2013.

[14] 刘东海,宋洪兰.水电工程EPC项目总承包商风险分析与综合评价[J].水科学与工程技术,2010(1):74-76.

[15] 陈志鼎,刘豪,肖芳.水电工程EPC项目采购风险评估[J].人民长江,2015,46(5):109-112.

[16] 李卉.基于三角模糊数的水利水电EPC项目投标风险评价模型研究[J].水利水电技术,2016,47(11):55-60.

[17] 赵美玲,陈进,易欣.基于TOC和SPA的水电EPC项目风险管理[J].土木工程与管理学报,2017,34(3):103-107.

[18] CHARNES A, GRANOT D. Prior solutions: extensions of convex nucleus solutions to chance-constrained games[C]∥Proceedings of the Computer Science and Statistics Seventh Symposium at Iowa State University.[S.l.]:[s.n.], 1973:323-332.

[19] SUIJS J, BORM P, WAEGENAERE A D, et al. Cooperative games with stochastic payoffs[J]. European Journal of Operational Research, 1995,113(1):193-205.

[20] TIMMER J, BORM P, TIJS S. On three shapley-like solutions for cooperative games with random payoffs[J]. International Journal of Game Theory,2004,32(4):595-613.

[21] TANIMOTO K, OKADA N, TATANO H.Project risk allocation through contingent cost allocation[C]∥2000 IEEE International Conference on Systems, Man, and Cybernetics.[S.l.]:[s.n.],2000:512-517.

ResearchonRiskSharingofEPCProjectofHydropowerProjectBasedonRandomCooperativeGame

WANGNa,HOUManman

The EPC project of hydropower project has the characteristics of large engineering, construction complexity and influence of the overall situation, which directly determines the risk that the participant will face many risks in the project implementation process. Reasonable risk sharing can not only meet the maximum effectiveness of the participants, but also improve the level of risk management. In view of this, the stochastic cooperative game theory is used to construct the optimal cooperative game model among the participants, and the risk transfer between the two sides is realized on the basis of the risk preference of the participant. The results show that the model can determine the proportion of the optimal risk sharing among the participants, and reduce the total risk of the project after the risk transfer, and realize the cooperation efficiency.

hydropower project; EPC project; risk sharing; random cooperation game

2095-3852(2017)06-0695-05

A

2017-07-13.

王娜(1993-)，女，河北邢台人，河海大学工程管理研究所硕士研究生，主要研究方向为风险管理.

国家自然科学基金项目(71402045).

F283

10.3963/j.issn.2095-3852.2017.06.010

WANGNa:Postgraduate; Institute of Engineering Management,Hohai University, Nanjing 211100, China.