漫谈函数模块中的相关概念教学

☉江苏省张家港市沙洲中学 何燕萍

漫谈函数模块中的相关概念教学

☉江苏省张家港市沙洲中学 何燕萍

概念教学是数学教学的难点和重点，也是不少学生学习不太重视的地方.很多学生或许会认为学好数学关键是要会做题目，数学概念无非就是几个公式，几个定理，有什么重要的，其实每个数学概念都有其深刻严谨的思想内涵，是构建数学大厦的基础，近年来的高考试卷也很好地考查了数学概念，涉及数学概念的考题清楚明了，又有一定的深度.由此，在平常的教学中，应该重视概念教学，这会让我们不断丰富自己的知识架构，并能通过本质思考更深的现象.

笔者所在学校的学生普遍数学基础薄弱，尤其在接受能力上，与优秀学生相比确实存在着一定差距，那么怎样才能够挖掘这部分学生的潜力？笔者思考：提高学生的数学能力，取得最为高效的学习效果，在课堂上究竟是应突出概念教学？还是要以解题教学为主？这值得教师探究.本文结合一下笔者在平常教学中遇到的问题，谈谈对于函数模块中有关概念教学的一些认识和做法，与读者交流.

一、重视对概念本质的理解

一直在思考这样一个问题，为什么学生对于数学概念遗忘得那么快，特别经过一段时间后，学生似乎对每个数学概念都得要重新认识，笔者认为，归根结底是学生没有很好地理解数学概念和数学思想，他们只是掌握了表面，在做题时也只是注重模仿，一旦稍有变化，就手足无措了，因此需要全方位地理解数学概念.要理解数学概念，首先需要注重数学语言文字符号的理解.

数学概念都是用文字或数学符号叙述的，尤其是语言文字，描述时不仅准确，而且精炼简明，因此对于数学概念的辨析上，要深深体会每句话的表达意思，有时甚至要达到”咬文嚼字”的地步.

案例1：函数的单调性.

单调性是函数三大性质之首，也是学生第一个学习的函数性质定义.用图像感官的认知是非常容易的，但是对于深刻理解单调性的定义还是需要一定的深思.教材对于单调性的定义是这样描述的：

设函数（fx）的定义域为I，如果对于定义域I内的某个区间D上的任意两个自变量的值x1，x2，当x1＜x2时，都有（fx1）＜（fx2），则称函数（fx）在区间D上是增函数；如果对于定义域I内的某个区间D上的任意两个自变量的值x1，x2，当x1＜x2时，都有（fx1）＞（fx2），则称函数（fx）在区间D上是减函数.

定义中关键是要理解“任意两个自变量的值x1，x2，当x1＜x2时，都有（fx1）＜（fx2）”这句话的含义，尤其是“任意”，“都有”这些文字怎么把握，例如，很多学生对于y=在定义域上的单调性如何描述感到非常困惑，经常问这样一个问题，到底什么时候可以用“∪”，什么时候又只能用和或逗号隔开，其实要突破这个难点，关键还是要逐字逐句理解单调性的定义，如果回答在定义域（-∞，0）∪（0，+∞）上为减函数，那根据单调性的定义，任意在这个区间上取x1，x2，当x1＜x2时，都有（fx1）＞（fx2），比如，取x1=-1，x2=1，满足x1＜x2，但（fx1）＜（fx2），但取x1=1，x2=2，却满足（fx1）＞（fx2），因此这样的回答是错误的，没有满足定义中“任意”和“都有”的条件，正确的回答应该是在（-∞，0）和（0，+∞）上均为减函数.

二、多角度构建问题分析概念

对于数学概念作进一步理解，应该从多角度去把握，也可以从正面辨析和反面比较，尤其是一些较抽象的数学概念，要构建一系列问题，从问题的解决中，使学生逐步对数学概念有一个准确、深刻的理解.

案例2：函数的概念.

函数概念是中学数学最为重要的概念.对于教学的实现手段，一般采用了丰富的概念模型，让学生从头脑中建立对应的关系，从而深刻体会这种变量间相互依赖的重要模型，最后用数学的语言进行了表述和总结.在函数学习中，为了刻画深刻和理解到位，在学习中需要积极体会函数的三个要素，其目的还是要让学生了解函数这个抽象的概念：

设A、B是非空的数集，如果按某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作y=f（x），x∈A.其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合｛f（x）|x∈A｝叫做函数的值域.

让学生仅仅从文字上去理解，由于描述的比较抽象，显然不能达到好的效果，应该设计一些问题，促进学生对函数概念的思考，从而帮助学生理解：

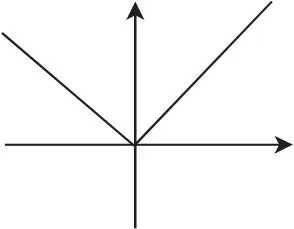
图1

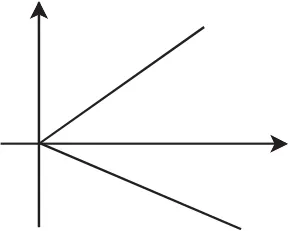
图2

问题1：以上两个图像（图1和图2）是不是函数的图像？

问题2：y=1与y=0·x+1是不是同一个关于x的函数？

问题3：y=x2+1与y=t2+1是不是同一个函数？

问题5：y=x2，x∈｛-1，0，1｝与y=|x|，x∈｛-1，0，1｝是否为相同的函数？

建立上述合适的问题变式，通过一系列问题变式，加强学生对于函数概念外延和内涵的认识.笔者认为，可以通过学生的辨析讨论，一起弄清上述问题，进而在问题的解决过程中，进一步让学生讨论更深层次的问题：“函数的对应关系，只强调结果不强调过程”，“函数即解析式”，“对应关系即运算关系”，“对应关系与函数图像”等，并帮助学生判别哪些是正确的？哪些是有问题的？从不同的角度分析讨论，从而在学生脑海中形成一个准确直观的函数概念.

三、数学概念教学的延伸

学生学习了数学概念，接下来就要学会能正确运用数学概念去解决实际问题，学生在运用时常会遇到两方面的困难：一是不知道该用哪种数学概念；二是用错数学概念.

案例3：对于定义域为D的函数y=f（x），若同时满足下列条件：①f（x）在D内单调递增或单调递减；②存在区间［a，b］⊆D，使f（x）在［a，b］上的值域为［a，b］，那么把y=f（x）（x∈D）叫闭函数.求闭函数y=-x3符合条件②的区间［a，b］.

很多学生在碰到一些新的概念或新的题型往往束手无策，不知道如何运用已经学过的知识来解决，比如上面提出的新概念：闭函数，学生不能很好地理解，觉得无从下手，其实只要抓住新概念定义的两个条件：①（fx）在D内单调递增或单调递减，那么y=-x3在（-∞，+∞）上单调递减，考查的是函数的单调性；②存在区间［a，b］⊆D，使（fx）在［a，b］上的值域为［a，b］，那么把y=（fx）（x∈D）叫闭函数，函数既然在实数域上是个减函数，要保证［a，b］上的值域为［a，b］，那么当x=a时，y=b，而当x=b时，y=a，根据这个关系列出方程，就能解出a，b的值，考查的是函数的值域问题，其实就是要学生回答：当x取何值时，函数能够取到最大值和最小值，整个题目还是要求学生掌握函数的单调性、值域、最值等概念，只不过换了一种新的形式——闭函数来考查.

案例4：已知函数是奇函数，且，求函数（fx）的解析式.

学生在解答这道题时认为（fx）是奇函数，那么（f0）=0，从而得到q=0，虽然跟答案一致，但是这样的解法是错误的，因为最后的函数解析式应为，即当x=0时，分母为0，（fx）无意义，正确的做法应是根据奇函数的概念，（f-x）=-（fx），列出，解出q=0，在根据，解出p=2，从而得到函数解析式，学生错误地利用了奇函数（f0）=0的概念，如果要利用这个条件，必须要满足x=0时函数有意义才行，因此在运用数学概念解题时，一定要求学生注意分析概念应用是否有前提条件，有没有符合该题目的具体情况.

数学概念教学是数学教学的重要组成部分，数学概念学得好不好，直接关系到学生数学能力的培养，在平常教学中，应努力把一个个数学概念讲得浅显易懂，分析透彻，那么学生在接下来的习题训练中就能取得效果，如果学生对数学概念理解不深刻，那么做再多的题目也只是掌握表面，稍加变动，就不知如何解答了，因此，作为数学教师，应该重视数学概念的教学，使学生学好数学概念，更重要的是用好数学概念.

1.王尚志.数学教学研究与案例［M］.北京：高等教育出版社，2006.

2.陈令深.探索新课改下数学教学的新模式［J］.中学数学教育，2005.

3.赵荣夫.新课程理念下实现学生思维参与的途径［J］.教育探索，2007.

4.中华人民共和国教育部制订.普通高中数学课程标准［S］.北京：人民教育出版社，2003.