一种多智能体协同信息一致性算法

陈旿，张鑫，金鑫，李泽宏，洪亮

西北工业大学 自动化学院，西安 710072

一种多智能体协同信息一致性算法

陈旿*，张鑫，金鑫，李泽宏，洪亮

西北工业大学 自动化学院，西安 710072

以无人机(UAVs)/导弹集群为代表的多智能体协同作战在未来战场中占有重要地位。协同信息的共享和一致性是多智能体系统完成协同、编队、集结、同步等协同任务的关键基础和前提。首先,基于邻居系统和团势能建立了信息一致性模型，将多智能体的协同信息的偏差映射为团势能。然后，通过以并行能量最小化求解马尔可夫随机场最大后验概率的方法实现了分布式无中心条件下的协同信息一致性。与传统的一致性算法相比，所提出的算法引入了虚拟基准的概念。当无外部基准输入时，基于平均场方法，通过邻居之间的协同信息交互建立虚拟基准；当存在领航节点或虚拟领航节点时，将领航节点协同信息的状态及状态导数作为虚拟基准。仿真结果表明:所得出的算法具有对网络规模不敏感、快速收敛、高鲁棒性的优点;对有/无基准输入的情况可采用相同的算法，体现了算法具有较好的适应性。

多智能体；一致性；马尔可夫随机场；平均场；虚拟基准

随着电子技术、计算机网络技术的发展，复杂大系统日益成为控制系统的主要形式。采用集中式控制存在计算量大、故障率高、鲁棒性低的缺点。多智能体系统具有灵活性高、易扩展、易维护、低成本的优点，所以将集中式复杂大系统的结构形式替换为可分离的简单智能体小模块协作控制的结构形式已经逐渐成为控制领域的一个研究热点[1]。多智能体系统是指局部之间可以相互作用的、由大量简单个体所组成的复杂网络系统[2]。多智能体系统的主要控制目标是通过分布式协议，在没有组织者和协调者的情况下，使各个智能体的状态达到一致[1-3]。多智能体协同信息一致性问题的最典型应用是无人航行平台的集群协调控制问题。同时，一致性问题也是解决集结问题、编队问题、同步问题、聚集问题、分布式估计、分布式最优化等问题的基础。近十年来，世界各国学者对一致性算法进行研究并得到大量研究成果。

所谓一致性问题是指所有智能体的状态在分布式协议的作用下，渐近地达到一个相同的协调值[1]。一致性问题起源于分布式计算、分布式决策和统计物理学。其研究可追溯至20世纪80年代的分布式决策问题(Distributed Decision-Making Problems)[4-5]，1992年，Benediktsson首次将统计一致性方法应用于传感器网络的信息融合中[6]。Vicsek在1995年从统计力学的角度出发，建立了一个一致性动力性模型，仿真结果表明，整个群体中的个体将会在行为上趋向一致[7]。Jadbabaie等在2003年发表文章，运用图论和Markov链对Vicsek模型进行了严格理论证明，结论表明当网络拓扑在有限时间内为无向连通图时，所有状态将趋于一致[8]。这篇文章引发了对一致性问题研究的热潮，此后涌现了大量的关于一致性算法的研究成果。一些知名的国际期刊专门出版了关于一致性问题的特刊[9-13]。较为代表性的研究成果有：Ren的研究结论指出在动态拓扑网络中，系统取得一致性的条件是有向通信网络是强连通的并包含有一簇有向生成树[14]；Li给出了含有异构子系统的多智能体系统收敛到一致的充分必要条件[15]。文献[16]研究了有噪声测量和传输延迟条件下的一致性问题。近年来一致性算法已经在无人航行器的编队控制[17]、智能交通[18]、传感器网络信息融合[19]、网络时钟同步[20]等多个领域得到广泛应用，成为系统与控制领域的一个重要研究课题。

尽管现有的分布式一致性算法主要应用在编队、聚集和跟踪上，但是算法研究的动力学模型已经从最开始假设的理想的线性系统转变成模拟实际环境的非线性系统，其中线性系统一般分为一阶线性系统、二阶线性系统和高阶线性系统；非线性系统一般分为多拉格朗日系统和刚体姿态系统等，因而分布式一致性算法需要开始考虑智能体自身的动态特性以及现实复杂环境对多智能体系统的影响。

多智能体系统通过邻居节点进行信息交换是达成一致性的关键，而现实网络存在的约束条件可以被大致分成两类，一类是通信信道的约束问题：时延、丢包、通信带宽、测量噪声等；另一类是多智能体网络拓扑结构变化问题。常见的分析方法主要包括：矩阵论方法、李雅普洛夫泛函方法和频域分析法等。

无人航行体编队与协同控制是多智能体一致性算法的一个重要应用领域和发展方向。无人航行体，如无人机、飞航弹，以一定的数量规模编队实施协同作战是“网络中心战”的重要模式之一。与单架或无协同关系的无人航行体相比，多航行体协同作战可以提高突防能力、电子对抗能力、对低可探测目标的搜索能力，同时减少战斗消耗，提高无人航行体的整体作战能力[21]。无人航行体编队与协同控制对信息一致性有其特殊的需求：首先，无人航行平台协同作战需要在一定指定的时间段内完成，这就要求多智能体之间的协同信息应当在有限时间内达到一致；其次，无人航行体编队根据作战任务的不同，对编队规模大小的需求也不同。比如导弹自主编队的规模可分为节数在2～9个之间的邻接规模编队、节数在9～18个之间的小规模编队、节数在18～36个之间的中等规模编队、节点数在36～72个之间的大规模编队与节点数大于72个的超大规模编队[21]。这些不同规模的导弹编队具有基本相同的作战周期和制导周期，要求能在基本相同的时间周期内达到信息一致性。再次，无人航行体编队协同作战工作在一定的对抗环境中，存在节点损失和新节点加入的情况，甚至有编队拆分和合并的情况存在，这造成了高度动态的通信拓扑结构，且通信时延不确定。这就对信息一致性算法的鲁棒性有较高要求，即在动态网络拓扑及不完全通信条件下，信息一致性的收敛性能基本保持不变。最后，时空配准是多无人航行平台执行协同任务的前提，时钟同步是多无人航行平台编队与协同作战最基本、最重要的一致性信息。

现有的分布式一致性算法基本是都是渐近算法，在理论上需要无穷长的时间才能达到信息一致性。目前在实际应用中，一般是通过指定一个收敛周期来解决无穷长收敛时间的问题[21]。此外，无人航行平台协同作战编队具有不同的编队规模，现有的一致性算法的收敛时间会随着编队规模的增加快速增加，较难满足不同编队规模条件下收敛时间基本一致的要求。最后，现有的信息一致性算法大部分是通过邻居节点之间进行信息交互达到一致的，不依赖于中心节点，对动态网络拓扑具有良好的适应性。

本文针对无人航行体编队所面对的上述问题，提出了一种基于平均场的分布式协同一致性算法。该算法在不同网络规模下的收敛时间基本保持不变，精度高，且对动态拓扑及丢包有很好的适应性。该方法也可以应用到其他多智能体的信息一致性场合，如分布式融合估计等[22]。

1 问题描述

一致性是指多个智能体对所关心的协同变量的取值达成共识。记该协同变量为信息状态x。假设在多智能体编队中有n个智能体，在本文余下的部分中，将统一以节点表示智能体编队中的个体。编队的通信拓扑可以用有向图G=(V,E)来表示，其中V={v1,v2,…,vn}表示节点的集合，E⊆V×V表示节点间链路的集合。现有的多智能体信息一致性的定义如下：

如果对于一个多智能体编队中所有节点的协同信息状态x=[x1,x2,…,xn] 都有式(1)成立：

(1)

则称多智能体编队达到一致性。

2 信息一致性模型

为了便于描述信息一致性模型，首先给出邻域系统的定义。一个邻域系统N可以定义为

N=Ni|∀i∈V

(2)

式中：Ni为节点i的邻居节点集合，其相邻关系具有如下特性[23]：

1) 任意给定一点i与其自身并不构成邻居关系：i∉Ni。

2) 相邻关系是相互的。

i∈Nj⟸⟹j∈Ni

如果式(1)成立，则称智能体编队中任意两个互为邻居的节点达成信息状态一致。由于智能体编队中节点数目为有限多个，若其中任意互为邻居界节点的两个节点信息达成一致，则智能体编队达到一致。因此，可以通过任意节点和与其有直接通信关系的所有邻居节点相互作用，达到节点之间信息一致，进而实现智能体编队的协同信息一致性。这种方法也符合智能体编队的实际工作场景，可以降低网络负载，同时降低节点被无线探测到的机率。故信息一致性模型可以描述为

(3)

式(3)所产生的一致性收敛点取决于编队节点初始信息状态，是一个动态变化的值。为了优化一致性算法的收敛性能，引入了一个虚拟基准的概念。在引入虚拟基准后，智能体编队中的节点不仅要与邻居节点实现一致，也要与虚拟基准实现一致。则式(3)应改写为

i=1,2,…,n;j∈Ni

(4)

式中：〈xR〉i为节点i的虚拟基准：当系统不存在指定基准，虚拟基准由邻居节点的平均作用获得，参见式(21)；若系统存在外部指定基准时，虚拟基准取值为外部基准值，见本文第3节。

由以上分析可知，式(3)和式(4)给出的信息一致性算法，只需要相邻节点之间的相互作用，即任意一个节点的信息状态仅仅依赖于其邻居节点的信息状态。因此，信息一致性的过程具有空间马尔可夫性。本文将基于空间马尔可夫随机场建立信息一致性模型。通过引入邻居系统和团势能，得到基于伊辛模型的能量函数，以能量最小化寻优的方法实现分布式信息一致性。

在基于空间的马尔可夫随机场建立的信息一致性模型中，本文用团来模拟邻居节点间关系。与子图的定义一致，可以定义单节点团C1、双邻居节点团C2、三邻居节点团C3等。本文所使用的单节点团C1、双邻居节点团C2为

C1=i|i∈V

(5)

C2=i,j|i∈V,j∈Ni

(6)

为每个节点设置一个初始信息状态，即为网络中的每个节点分配一个初始的协同信息，这一事件可视为一个标签化的过程，分配标签在随机领域术语中被称为配置。所谓的标签化，就是从标签集合中分配一个标签给每个节点。根据集合的定义，将系统产生的所有协同信息称为一个标签集合，它可以是连续或者离散的。在协同信息一致性系统中，本文采用连续的标签集合。故在所建立的空间马尔可夫随机场信息一致性模型中，系统中所有节点应具有相同的标签集合，与之对应的配置空间为

X=X1,X2,…,Xn∈Rn

(7)

式中：n为网络中节点的个数。标签化Xi=xi表示为每个节点i配置一个初始协同变量值xi这一事件，对应的标签集合可以表示为{X1=x1,X2=x2,…,Xn=xn}，记为X=x，其中x是X的一个配置。在概率中，x是一个联合事件，其概率记为Px；同理，在配置过程中，将节点i获得初始协同变量值xi这一事件的概率记为P(xi)。由联合概率的基本性质可知以下两个条件显然成立：

P(x)>0, ∀x∈X

(8)

Pxi|xV-i=Pxi|xNi

(9)

式(8)和式(9)分别体现了概率事件的正定性和概率事件的马尔可夫性。对于邻域系统N而言，X是在G上的马尔可夫随机场。

存在这种情况，当系统每个节点都获得相同的标签，即

xi=x,i∈V

(10)

认为整个系统达到了信息一致，实现了全网络的协同信息一致性。其中事件xi=x的概率Pxi=x，可以通过调整网络的配置来使其取得最大值。

在马尔可夫随机场中，寻找Pxi=x的最大概率定义为寻找马尔可夫随机场的最大后验概率(Maximum A Posteriori，MAP)配置。文献[23]指出，马尔可夫随机场等同于吉布斯随机场，故协同信息配置也应该服从以下形式的吉布斯分布：

(11)

(12)

由式(12)可知，U(x)为所有可能的团C上的团势能Vcx之和[24]。进一步写为

(13)

只定义C1团和C2团，故式(13)简化为

(14)

引入式(11)，易知能量函数Ux的最小化使Px的概率值最大化。

问题转化为求最小化能量函数U(x)，引入平均场理论中的伊辛模型，模型中的总能量可以表示为[25]

(15)

式中：H为强度系数；J为耦合矩阵；xi对应于节点i的本地协同信息集合。耦合矩阵J的每个格点都代表一对邻居节点之间的相互作用关系，若节点i和j之间可以进行协同信息交互，则矩阵中Jij不为0。式(15)能量函数U(x)最小化等价于P(x)的概率值最大。

以上分析表明，在式(11)的作用下，基于式(4)的一致性问题与平均场问题是等价的。可以通过求平均场能量最小化来求解一致性的解，同时也给出了一个思路，可以通过平均场给出虚拟信息基准。

2.1 能量函数定义

作为一致性算法的目标函数，能量函数是可以被最小化的，它主要有以下两个任务：

1) 定义协同信息变量达成一致的最佳求解方案。

2) 通过能量最小化寻找最佳的虚拟协同信息基准。

从式(14)中可知，团的势能函数求和可得势能函数。参考文献[24]，本文将双邻居节点团C2的势能函数定义为

V2xi,xj=gxi-xj

(16)

式中：gxi-xj为节点i和j之间的状态偏差的单调递减惩罚函数。在惩罚函数中最常用的是二次函数，因此式(16)可改写为

gxi-xj=xi-xj2

(17)

在高对抗的实际工作环境中，节点的状态是不断变化的，随时都有可能发生某一个节点故障重启或加入一个新节点，此时故障重启和新加入的节点将重新获取初始协同信息变量，这与其他节点同一时刻的信息变量存在较大的状态偏差，因此会产生一个较大的修复因子，使一致性集结点产生较大的波动，进而影响能量最小化的时间，降低算法效率。为此，引入一个截断变量σ，用来表示节点与其邻居节点之间的状态偏差的方差。式(17)可以重写为

g(xi-xj)=min{σ2,(xi-xj)2}

(18)

对式(18)求导可得

g′(xi-xj)=2×min{σ,(xi-xj)}

(19)

而单节点团C1的势能函数仅仅依赖节点当前信息状态与系统参考基准状态的偏差，故其二次方程描述为

V1xi=xi-xR2

(20)

式中：xR为基准信息,取值取决于多智能体系统的工作模式。多智能体系统的工作模式基本可以分为两类，一类是智能体系统不存在外部基准信息，由各智能体在一致性协议的作用下，协同变量收敛于某个值，该值由各智能体协同变量的初值决定。在这种情况下，xR的取值由式(21)给出平均场算法计算得到；另一种是存在基准信息，不仅要求智能体协作变量收敛，而且要收敛于给定的基准信息，例如存在领航节点的无人航行体编队飞行。在这种情况下，xR的取值取为外部给定的基准信息。

根据平均场理论，其他所有节点对某一个给定节点的影响可由一个平均作用近似获取[26]，进一步计算可得领域系统的基准信息状态。在平均场中，节点i邻域系统的虚拟基准状态可以定义为

(21)

式中：P(xj)为配置过程中节点j获得初始协同变量值xj的概率，将式(18)、式(20)代入式(14)可得完整的能量函数表达式为

(22)

由第2节分析有：当U(x)取得最小值Umin(x)时就得到了全局系统信息一致的最优点。上述问题就转化为求式(22)的最小值点问题。式(22)的含义为： 通过对系统中每个节点的团势能求和，将能量函数U(x) 转化为一个全局的变量并寻找最小化的能量函数Umin(x)，这是一个简单的二次函数求最值问题。但在分布式多跳网络中，获取每个节点的团势能并求和会产生很大的网络负载，增加网络中信息交互的时间，这可能会导致节点所获取的一致信息过时。解决这一问题，应该寻找一种分布式并行运行算法，减少信息在网络中的传输时间，降低网络负载，更加快速准确地获取能量函数最小化值。

2.2 能量函数的并行最小化

为了解决一致性过程中新入节点或重启节点与邻居节点之间协同变量偏差过大问题，在式(18)中引入了截断因子σ，这使得能量函数不再是一个线性函数，为简化分析，考虑公式：

(23)

式(23)可以看作是对两个二次函数的求和。由二次函数的基本性质可知当U(x)取最小值时，x为函数的一个驻点，该点处的导数(梯度向量)值必为0，即

(24)

式(24)与式(22)具有较高的一致性。在求和的过程中依旧要获取系统中每个节点的协同变量信息，会增加系统的计算量，增大网络负载，增加网络延迟。故对式(24)进行整理写为

(25)

令

(26)

从而有

(27)

式(27)表明，全局能量函数最小化问题等价于借助式(27)求各个节点能量最小化问题。同时并行的对各个节点进行团势能更新，以期取得最小的能量函数值，最终实现全局能量函数最小化。采用式(27)全分布式能量最小化算法，能较好地解决网络节点多、跳数多产生的网络负载过重问题。

为达到协同变量一致性，使全局能量函数最小化，式(25)取得了一个局部最小值点x。式(17)所定义的能量函数是一个二次函数，其基本性质决定了式(25)在定义域内是一个严格的凸函数。进一步由凸函数的性质有：严格的凸函数在全局中最多只有一个全局最小值点[27]。故式(25)取得的局部最小值点x即全局最小值点，在这点处可以取得马尔可夫随机场的最大后验概率MAP。

在实际应用中，能量最小化函数的算法采用下面规则进行迭代求解：

(28)

式中：μ为一个较小的常数,μ的取值参考具体实验精度要求和数值积分步长要求。由于式(28)仅涉及简单的算术运算和初等函数运算，因此本文的分布式信息一致性算法复杂度低，适用于CPU能力和功率都十分有限的无线自组织网络节点。

2.3 一致性算法收敛性分析

定理1多智能体编队在式(28)的作用下，将达到信息一致性。

证明：

式(28)可改写为

(29)

式中：μ为一个较小的常数可视为微分项中的步长，步长越小，其佩亚诺余项越小，从而扰动变小，当μ趋近于无穷小时，差分算子可视为微分算子。现实中计算机系统往往是非线性的离散系统，可以将式(28)的离散系统抽象成连续微分方程，从而达到用线性系统逼近非线性系统的目的。

平均场方法的更新方程可写为

(30)

引入式(21)，式(30)可改写为

(31)

引入邻接矩阵，将式(31)改写为

(32)

式中：aij为邻接矩阵的元素。

合并同类项，可得

(33)

矩阵方式为

(34)

式中：

(35)

显然，-L为对角占优矩阵，零为其简单特征根[14]，故系统收敛。或L具有正实部特征根，则-L具有负实部特征根，所以系统收敛[14]。

定理2收敛速度一致性

下面对有向通信拓扑下本算法的收敛速度进行分析，由文献[28]可知，分布式多智能体系统一致性算法的收敛速度由其通信拓扑图的代数连通度决定，即矩阵L的第二小特征值，或矩阵L的谱半径ρ(L)。本文一致性算法可写为

(36)

系统状态方程为

(37)

对式(37)进行拉普拉斯变换可以得到

sx(s)=-Lx(s)

(38)

x(s)的特征方程为

det(sIn+L)=0

(39)

由于有向通信拓扑图Gn含有一个生成树，且L为拉普拉斯矩阵，从而由文献[29]可知L的特征值应为

0=λ1(G)<λ2(G)≤…≤λn(G)

(40)

式中：λn(G)为图Gn的谱半径，通常认为拉普拉斯矩阵：

(41)

为图的Gn代数连通度，恒大于零。此时除了一个特征根为0外，其他特征根均有负实部，即均位于左半平面上，因而系统可以收敛到一个稳定状态。

再次，由文献[27,30-31]可知

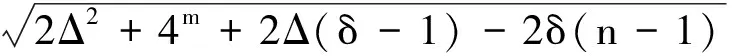
(42)

式中：Δ、δ为图Gn的最大度和最小度；m、n分别为边数和顶点数。等号成立当且仅当图为正则偶图。

λ2(G)≤v(G)≤e(G)

(43)

式中：v(G)为点连通度；e(G)为边连通度。

进而在图为固定直径d的n阶连通图中有

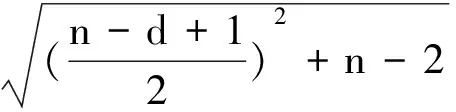
(44)

综上，当多智能体收敛到稳定状态时，由于队形和节点间为了避免碰撞引入的间距已经被设定好，其第二小特征值的上界的增长速率由于幂函数特性也趋于稳定，特征根最后应分布在一个相对固定区间中，所以整个系统的收敛速度变化也集中在一个浮动不明显区间内，因而即使算法应用规模扩大即节点个数增加，算法收敛速度依旧无明显增大。

3 扩展到有基准状态的一致性信息一致性模型

和现有的大部分一致性算法一样，式(29)所给出的信息一致性算法适用于完全没有中心节点，或没有指定基准值的场合。如没有指定集结位置的编队协同、多导弹同时击中目标的饱和攻击中对于协同末制导中的时间一致性等。但很多实际应用还是存在一个基准(期望)信息状态，这时，不仅要求编队收敛于一个共同值，而且该共同值要收敛于一个指定的基准状态。因此需要建立一种一致性算法，使得编队中的每一个智能体的协同信息状态一致于一个时变的或时不变的基准状态[32]。一种合理的应用场景是，在智能体编队中有一个智能体作为领航节点，通过特殊链路受控于指挥中心，获得基准信息状态。编队中的其他智能体通过与领航节点实现信息一致达到与基准信息状态的一致。即通常所说的领航-跟随模型。不失一般性，设节点1为领航节点，xr为基准信息状态，xr关于时间t是有界且分段连续的。在此条件下，一致性问题可以描述为

(45)

(46)

定理3在有基准信息状态条件下，式(29)收敛到基准值的必要条件是有向图Gn含有一簇生成树。

证明：

假设有向图Gn不含有一簇有向生成树，则存在一个航行体将整个航行体编队分成两个互不交换信息的子编队，或至少存在两个不接受信息的子编队。

情况1假设第1个子编队有x个节点，第2个子编队有y个节点，x+y=n-1。节点1到x在编队1，节点x+2到y在编队2，中间节点为x+1，矩阵L可改写为

(47)

式中：Lx∈Rx×x，Ly∈Ry×y，lx=[lx+1,1,lx+1,2…,lx+1,x]，ly=lx+1,x+2,lx+1,x+3,…,lx+1,n。

由定理1中转化得到

(48)

故Lx、Ly矩阵行和为0；因而至少有一个零特征值。且Rank(Lx)≤x-1，Rank(Ly)≤y-1。可得Rank(L)≤n-2，即矩阵L至少有两个零特征值。

情况2矩阵L至少有两行元素均为零，即矩阵L至少有两个零特征值。

两种情况均与拉普拉斯矩阵含有一簇有向生成树后有且仅有一个零特征值矛盾。

4 仿真验证

为了验证本文所提出算法的有效性，将在MATLAB 2009b的环境下建立分别具有3×3通信拓扑9个节点的邻接规模编队、7×7通信拓扑49个节点的大规模编队，形成标准2D网格结构，仿真结果中不同颜色曲线分别表示各节点的状态。为简单起见，假设每一节点仅与其水平或邻居节点进行交互，即采用标准的4-邻居系统。各节点与邻居节点交换协同变量并更新自己的变量信息状态。本节分别针对多智能体在无基准信息状态下的信息一致性、存在静态基准信息状态的信息一致性、存在动态基准信息状态的信息一致性等问题，对本文算法的性能进行仿真验证，并与极大一致性算法进行对比分析。极大一致性算法可以表示为

ui(t)=αi[(1-μ)(xmax(t)-xi(t))+

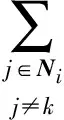
(49)

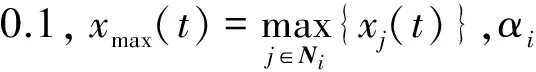
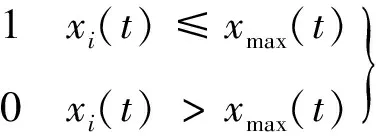
(50)

4.1 无基准信息状态下的分布式算法仿真分析

图1(a)和图1(b)分别展示了本文算法在3×3、7×7通信拓扑条件下，全局各节点之间协同信息的变化情况。在没有外部基准信息，设定丢包率小于30%的情况下，所有节点的协同信息差值收敛于0值，且与理想实验环境下无明显差别，这表明邻居节点之间关于协同信息的误差已达到可接受范围之内。随着节点数目的增加，全网节点对协同变量达成共识的时间并未发生明显变化，这体现了该算法良好的鲁棒性。图1(c)和图1(d)分别展示了极大一致性算法在3×3、7×7通信拓扑条件下，全局各节点之间协同信息的变化情况。通过对比分析，本文算法在网络规模较小情况下与极大一致性算法收敛情况相似，但是随着网络规模的增大，本文算法在收敛时间方面具有明显优势。

4.2 外部静态基准信息状态下的分布式算法仿真分析

图2(a)和图2(b)分别展示了本文算法在不同编队规模下，各节点在有外部静态基准信息且设定丢包率小于30%时对协同变量达成共识：所有节点协同信息收敛于外部静态基准，或称为与外部基准信息之间的差值小于误差期望值(10-6)，可认为全局节点就收敛信息达成共识，即实现全网的协同信息一致性。与图1(a)和图1(b)比较易知，在有外部基准信息情况下，协同变量最终取值为外部基准，各节点的协同信息状态与外部基准信息误差小于所允许的最大误差。在收敛时间方面，随着节点数目的增加，全局节点达成信息共识的时间无明显增加。图2(c)和图2(d)分别展示了极大一致性算法在3×3、7×7通信拓扑条件下，全局各节点在有外部静态基准信息时协同信息的变化情况。与图2(a)和图2(b)比较分析，随着节点规模扩大，极大一致性算法的效率明显下降。

4.3 外部动态基准信息状态下的分布式算法仿真分析

图3的外部动态基准信息取值为幅值为1的正弦函数，丢包率设定为小于30%。代表本文算法的图3(a)和图3(b)与静态基准信息相比，节点初始信息状态与基准信息有较大的差值，当各节点与邻居节点相互交换自身协同信息并更新自己的信息状态以后，对局部协同变量的共识趋于虚拟基准，而虚拟基准趋于外部基准，与外部基准差值不断减少，最终所有节点跟随外部基准运动，实现全局协同信息一致性。图3(c)和图3(d)分别展示了极大一致性算法在3×3、7×7的网格拓扑条件下，存在外部动态基准信息时的仿真结果，可以看出，极大一致性算法收敛性能并不理想，偏差很大。

图3 有动态外部基准信息
Fig.3 With dynamic external reference information

4.4 QualNet平台下的信息一致性仿真

多智能体生存环境的对抗性决定了多智能体必须具有高度的协同能力。在实际使用环境中，时空配准是多无人机航行平台执行协同任务的前提，对协同信息达成共识是多无人机航行平台编队与协同作战最基本、最重要的一致性信息；无人航行体编队协同作战工作在一定的对抗环境中，存在节点损失和新节点加入的情况，甚至会有编队拆分与合并的情况，造成高度动态通信拓扑结构，且时延不确定，丢包率高，这就要求算法应该具有较强的鲁棒性。

本文用QualNet模拟多智能的实际生存环境，采用本文所提出的分布式协同一致性算法，在存在网络丢包的情况下，各节点通过本文提出的算法能够达到时钟同步。为更好的体现算法性能，在同等环境下对ATS (Average Time Synchronization)、GTSP (Gradient Time Synchronization Protocol)和本文算法MFTS (Mean Field based Time Synchronization)进行比较，结果如图4和图5所示。

首先给出判断达到信息一致性的标准：当全局系统中所有有效节点与邻居节点对协同信息的共识值之间的差值小于10-6时，就认为达到了全局信息的一致性。在图4中，分别对邻接规模(9个节点)编队、中等规模(25个节点)编队、大规模(64个节点)编队、超大规模(100个节点)编队进行对比。由图可知，GTSP算法仅仅在通信拓扑邻接规模能在指定的时间内实现全局信息信息一致性，随着节点数目的增多，算法的性能急剧下降；ATS算法虽然能够较好地完成多智能体信息一致性，但随着节点数目的增多，所需要一致性的时间不断地增大。图5为对不同节点数目，当采取3种不同算法时所需时间的直观表示。本文提出的MFTS能更好地适应动态拓扑，具有较高的鲁棒性。

图4 不同算法的性能比较
Fig.4 Comparison of performance of different algorithm

图5 不同节点数目时间比较
Fig.5 Comparison of time of different number of nodes

5 结 论

本文提出了一种多智能体协同信息一致性算法。

1) 该算法对网络规模不敏感，在不同的网络规模下，收敛时间基本保持不变。

2) 该算法对不完全通信网络有一定的适应性，仿真验证表明在网络丢包达到30%时，依然可以收敛。

3) 该算法实现简单，对于有基准、无基准、静态基准、动态基准均可采用同样的算法结构，具有很好的适应性。

[1] CAO Y, YU W, REN W, et al. An overview of recent progress in the study of distributed multi-agent coordination[J]. IEEE Transactions on Industrial Informatics, 2012, 9(1): 427-438.

[2] 王寅秋. 非线性多智能体系统一致性分布式控制[D]. 北京: 北京理工大学, 2015: 12-21.

WANG Y Q. Distributed consensus for non-linear multi-agent systems[D]. Beijing: Beijing Institute of Technology, 2015: 12-21 (in Chinese).

[3] 张庆杰. 基于一致性理论的多UAV分布式协同控制与状态估计方法[D]. 长沙: 国防科学技术大学,2011: 10-31.

ZHANG Q J. Distributed cooperative control and statement estimation for networked multiple UAVs based on consensus theory[D]. Changsha: National University of Defense Technology, 2011: 10-31 (in Chinese).

[4] TSITSIKLIS J N. Problems in decentralized decision making and computation[J]. Problems in Decentralized Decision Making & Computation, 1984, 43(9): 134-139.

[5] TSITSIKLIS J, BERTSEKAS D, ATHANS M. Distributed asynchronous deterministic and stochastic gradient optimization algorithms[J]. IEEE Transactions on Automatic Control, 1984, 31(9): 803-812.

[6] BENEDIKTSSON J A, SWAIN P H. Consensus theoretic classification methods[J]. IEEE Transactions on Systems Man & Cybernetics, 1992, 22(4): 688-704.

[7] VICSEK T, CZIRK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 75(6): 1226.

[8] JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001.

[9] HUSSEIN I I, STIPANOVIC D M. Effective coverage control for mobile sensor networks with guaranteed collision avoidance[J]. IEEE Transactions on Control Systems Technology, 2007, 15(4): 642-657.

[10] LEONARD N E, PALEY D A, LEKIEN F, et al. Collective motion, sensor networks, and ocean sampling[J]. Proceedings of the IEEE, 2007, 95(1): 48-74.

[11] MURRAY R M. Recent research in cooperative control of multivehicle systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2007, 129(5): 571-583.

[12] OLSHEVSKY A, TSITSIKLIS J N. Convergence speed in distributed consensus and averaging[J]. SIAM Journal on Control and Optimization, 2009, 48(1): 33-55.

[13] HOLSAPPLE R W, KINGSTON D B. Cooperative control of autonomous systems[J]. International Journal of Robust and Nonlinear Control, 2011, 21(12): 1355-1357.

[14] REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.

[15] LI S, WANG J, LUO X, et al. A new framework of consensus protocol design for complex multi-agent systems[J]. Systems & Control Letters, 2011, 60(1): 19-26.

[16] LI T, ZHANG J F. Consensus conditions of multi-agent systems with time-varying topologies and stochastic communication noises[J]. IEEE Transactions on Automatic Control, 2010, 55(9): 2043-2057.

[17] BRAGINSKY B, BARUCH A, GUTERMAN H. Tracking of autonomous underwater vehicles using an autonomous surface vehicle with ranger interrogator system[C]∥OCEANS 2016 MTS/IEEE Monterey. Piscataway, NJ: IEEE Press, 2016: 1-5.

[18] THUSEETHAN S, VASANTHAPRIYAN S. Multi-agent based ocean-transport and traffic controlling system: A simulation[C]∥2015 5th National Symposium on Information Technology: Towards New Smart World (NSITNSW). Piscataway, NJ :IEEE Press, 2015: 1-5.

[19] VAZQUEZ-OLGUIN M, SHMALIY Y S, IBARRA-MANZANO O. Design of blind distributed UFIR filter based on average consensus for WSNs[C]∥ 2016 13th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE). Piscataway, NJ :IEEE Press, 2016: 1-6.

[20] BOLOGNANI S, CARLI R, LOVISARI E, et al. A randomized linear algorithm for clock synchronization in multi-agent systems[C]∥2012 IEEE 51st IEEE Conference on Decision and Control (CDC). Piscataway, NJ :IEEE Press, 2012: 20-25.

[21] 吴森堂. 导弹自主编队协同制导控制技术[M]. 北京: 国防工业出版社, 2015: 13-150.

WU S T.Cooperative guidance & control of missiles autonomous formation[M]. Beijing: National Defence Industry Press, 2015: 13-150(in Chinese).

[22] 曾斌, 姚路, 魏军. 基于平均场模型的传感器网络信息共享算法研究[J]. 传感技术学报, 2009 (10): 1486-1491.

ZENG B, YAO L, WEI J. A mean field model based information sharing algorithm for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2009 (10): 1486-1491 (in Chinese).

[23] LI S Z. Markov random field modeling in image analysis[M]. Berlin: Springer, 2009: 357.

[24] KOPETZ H, OCHSENREITER W. Clock synchronization in distributed real-time systems[J]. IEEE Transactions on Computers, 1987, 100(8): 933-940.

[26] GAST M. 802.11 无线网络权威指南[M]. 南京: 东南大学出版社, 2007: 52-53.

GAST M. 802.11 wireless networks: The definitive guide[M]. Nanjing: Southeast University Press, 2007: 52-53 (in Chinese).

[27] 丁尚文. 图的最大和次小拉普拉斯特征值[D].成都: 电子科技大学, 2008.

DING S W. The largest and the second smallest eigenvalue of graphs[D]. Chengdu: University of Electronic Science and Technology of China, 2008(in Chinese).

[28] OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.

[29] AYSAL T C, ORESHKIN B N, COATES M J. Accelerated distributed average consensus via localized node state prediction[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1563-1576.

[30] 刘瑞芳. 图的最小特征根和拉普拉斯谱半径[D]. 上海: 华东师范大学,2010.

LIU R F. The least eigenvalue and the laplacian spectral radius of graphs[D]. Shanghai: East China Normal University, 2010 (in Chinese).

[31] 汪天飞, 李彬. 图的最大拉普拉斯特征值的上界[J]. 四川师范大学学报(自然科学版), 2007, 30(2): 191-193.

WANG T F, LI B. New upper bounds for the laplacian spectral radius of graphs[J]. Journal of Sichuan Normal University (Natural Science), 2007, 30(2): 191-193(in Chinese).

[32] WEI R, RANDAL W D. 多智能体协同控制中的分布式一致性——理论与应用[M].北京：电子工业出版社，2014： 57-58.

WEI R, RANDAL W D. Distributed consensus in multi-vehicle cooperative control—Theory and applications[M]. Beijing: Publishing House of Electronics Industry, 2014:57-58(in Chinese).

Acooperativeinformationconsensusalgorithmformulti-agentsystem

CHENWu*,ZHANGXin,JINXin,LIZehong,HONGLiang

SchoolofAutomation,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Multi-agentcooperativeoperationplaysanimportantroleinthecyberspacewar,andthemainapplicationliesinthefieldofmultipleUnmannedAerialVehicles(UAVs)/multi-missilecollaborativecluster.Sharingcollaborativeinformationandconsistencyarethefoundationandprerequisiteforthemulti-agenttocompletecollaborativetaskssuchascoordination,formation,flockingandsynchronization.Aconsensusinformationmodelisestablishedbasedontheneighborsystemandtheclusterpotential,andthebiasofthecooperativeinformationismappedtotheclusterpotentialenergy.ByusingtheminimizationofparallelenergytosolvethemaximumaposterioriprobabilityoftheMarkovrandomfield,cooperativeinformationreachesaconsensuswithdistributedandnoncentercondition.Differentfromthetraditionalconsensusalgorithm,thealgorithmproposedintroducestheconceptofvirtualreference.Avirtualreferenceisestablishedbycooperativeinformationinteractionamongtheneighborsbyusingthemeanfieldtheorywithnoexternalreferenceinput.Whenthepilotnodeorthevirtualpilotnodeexists,thestateanditsderivativeofthepilotnodecooperativeinformationareusedasthevirtualreference.Simulationresultsshowthattheproposedalgorithmhastheadvantagesofinsensitivitytonetworkscale,fastconvergenceandhighrobustness.Thealgorithmcanbealsousedinthepresence/absenceofreferenceinput,meaningthatthealgorithmhasgreatadaptability.

multi-agent;consensus;Markovrandomfield;meanfield;virtualreference

2017-03-07；

2017-04-13；

2017-04-26；Publishedonline2017-05-121839

URL：http://hkxb.buaa.edu.cn/CN/html/20171220.html

MajorResearchProjectofShaanxiProvince(2017GY-069)

.E-mailchenwu@nwpu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321222

2017-03-07；退修日期2017-04-13；录用日期2017-04-26；网络出版时间2017-05-121839

http://hkxb.buaa.edu.cn/CN/html/20171220.html

陕西省重点研发计划(2017GY-069)

.E-mailchenwu@nwpu.edu.cn

陈旿，张鑫，金鑫，等．一种多智能体协同信息一致性算法J．航空学报,2017,38(12):321222.CHENW,ZHANGX,JINX,etal.Acooperativeinformationconsensusalgorithmformulti-agentsystemJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):321222.

TP273

A

1000-6893(2017)12-321222-13

苏磊)