表面裂纹疲劳扩展和寿命计算的高效高精度数值分析方法

柴国钟,吕君,鲍雨梅,姜献峰,丁浩

1.浙江工业大学 机械工程学院，杭州 310012 2.义乌工商职业技术学院 机电信息学院，义乌 322000

表面裂纹疲劳扩展和寿命计算的高效高精度数值分析方法

柴国钟1，*,吕君1, 2,鲍雨梅1,姜献峰1,丁浩1

1.浙江工业大学 机械工程学院，杭州 310012 2.义乌工商职业技术学院 机电信息学院，义乌 322000

基于弹性力学理论，建立了三维裂纹应力强度因子计算的混合边界元法基本理论和数值求解技术；针对表面裂纹疲劳扩展过程中，需要计算每个裂纹扩展步下的应力强度因子，从而需要重复计算大型非对称系数矩阵问题，提出了仅在初始裂纹状态下一次计算主控矩阵，对于随后的疲劳裂纹扩展，只需做非常小规模矩阵的计算，且以显式形式给出应力强度因子解而无需求解大型线性代数方程组的方法，大大提高了计算效率；针对疲劳裂纹扩展过程中，单元需要不断重新划分问题，由于混合边界元法中的主控矩阵与裂纹无关，故只需对裂纹表面单元进行重新划分，对半椭圆表面裂纹，由于将其映射到单位半圆上划分单元，而单位半圆上的单元在疲劳扩展过程中不变，从而通过映射关系自动重新划分裂纹表面单元。最后，通过若干算例和试验，考核了本文方法的精度和可靠性。本文的研究为工程结构表面裂纹疲劳扩展和寿命计算的高效高精度数值分析建立了理论基础和实现方法。

表面裂纹；疲劳扩展；高效高精度分析；混合边界元法；应力强度因子

表面裂纹是航天航空、机械、能源、海洋工程等装备和结构部件中最常见的缺陷形式[1]，其疲劳断裂也常常是这些装备破坏的主要原因之一，因此，表面裂纹的疲劳扩展和寿命分析也是工程结构强度分析的重要内容之一。

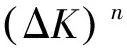
有限元法的主要优点是通用性强，可以分析任意几何形状受任意载荷的裂纹体，且精度高。其主要缺点是需要对整个裂纹体进行离散，用于表面裂纹疲劳扩展分析，由于疲劳扩展过程中裂纹形状和尺寸不断变化，对于每个裂纹扩展步，裂纹前沿单元都要重新划分和反复计算应力强度因子，非常繁杂，用于工程实际装备和结构的表面裂纹疲劳扩展和寿命分析具有很大的困难。

本文基于弹性力学理论，建立一种表面裂纹应力强度因子计算和疲劳扩展分析的混合边界元法基本原理和数值求解技术，该方法的主要优点是，只需在初始裂纹状态下对整个结构进行一次完整的数值计算，对于随后的每个疲劳裂纹扩展步，只需对裂纹表面单元(随着疲劳扩展自动跟进划分)做非常小规模矩阵的重复计算，且每一扩展步下计算的应力强度因子是“精确”(数值意义上)的。

若干算例和试验的考核表明，本文方法具有高效和高精度的优点。本文的研究为工程结构表面裂纹疲劳扩展和寿命计算的高效高精度数值分析建立了理论基础和实现方法。

1 基本理论与分析方法

1.1 混合边界元法

对于图1所示的三维表面裂纹体，混合边界积分方程为[10]

(1)

(2)

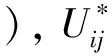
即当奇异点p位于非裂纹边界Г=ΓⅠ+ΓⅡ上时，采用利用单位力基本解(第一基本解)的第一类边界积分方程，而当奇异点p位于裂纹面ГC上时，采用利用单位位移不连续基本解(第二基本解)的第二类边界积分方程。

为了数值求解式(1)和式(2)，将图1所示裂纹体的整个边界离散划分为n个单元，即

式中：

(3)

(4)

图1 表面裂纹
Fig.1 Surface crack

将式(4)代入式(1)和式(2)，得到离散后的边界积分方程为

cij(p)uj(p)=

(5)

ti(p)=

(6)

将整个裂纹体边界分为图1所示3类，并采用相应的3类单元：第一类边界(通常边界ΓⅠ)——Ⅰ类单元；第二类边界(裂纹嘴上下边界(含裂纹扩展)ΓⅡ)——Ⅱ类单元；第三类边界(裂纹表面ГC)——裂纹单元。

第一类边界(通常边界ΓΙ)：采用通常的4-8节点等参元，单元形式如图2所示，其插值函数为Ni(ξ1,ξ2)(i=1,2,…,8)[11]。

因此单元内任一点的整体坐标、位移和面力可分别表示为

(7)

第二类边界(裂纹嘴上下边界(含裂纹扩展)ΓⅡ)：由于裂纹嘴上下表面位移不连续，因此不能采用与第一类边界相同的单元插值函数。本文对该类边界提出如下的非协调等参元。

图2 4-8节点等参元
Fig.2 Four-eight nodal iso-parameter element

图3 边界的非协调等参元
Fig.3 Incompatible iso-parameter element on boundary

边界的单元划分如图3(a)所示。对于单元1，将图2所示的通常的8节点单元的2、5节点向单元内移到ξ2=-1/2处；对于单元2，将节点1、5、2向单元内移到ξ2=-1/2处；对于单元3，将节点1、5向单元内移到ξ2=-1/2处，如图3(b)～图3(d)所示。

对于单元1有

(8a)

对于单元2有

(8b)

对于单元3有

(8c)

式中：Nl(l=1,2,…,8)为图2所示通常的4-8节点等参元插值函数。

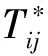
(9)

对于图5所示椭圆裂纹，其相对位移基本函数为

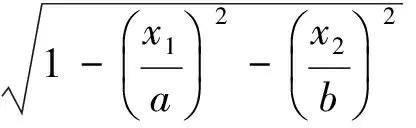
(10)

椭圆及部分椭圆裂纹是工程结构中最常见的三维裂纹，结构中的深埋裂纹通常可以简化成深埋椭圆裂纹，平板表面裂纹及圆筒中的轴向表面裂纹通常可以简化为半椭圆表面裂纹，孔边角裂纹通常可以简化为1/4椭圆表面裂纹等，而这些裂纹模型都可看做是图5所示椭圆裂纹中截取的一部分,因此它们的相对位移基本函数都可以用式(10)表示，只是对于不同的裂纹，它们的相对位移权函数不同。

然后利用式(9)将式(5)和式(6)中的最后一个积分项分别改写为

(11)

图4 平片裂纹
Fig.4 Planar crack

图5 椭圆裂纹
Fig.5 Elliptical crack

(12)

(13)

最后将式(13)代入式(12)，再返回式(5)和式(6)，式(5)和式(6)可进一步写为

图6 半线性权函数单元
Fig.6 Semi-linear weight function element

(14)

(15)

1.2 数值求解技术

由式(14)和式(15)可知，在离散形式的边界积分方程形成过程中，需计算大量的如式(16)～式(18)所示的奇异积分。

(16)

(17)

Sk∈ΓC

(18)

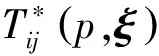
对于1/R的奇异积分式(16)和1/R2的奇异积分式(17)采用通常边界元中的方法解决[11]。

对于1/R3的超奇异性积分，首先将式(18)改写为

(19)

不失一般性，设单元Sk位于Ox1x2平面，n(p)=n(q)=(0,0,1),如图7所示。令

Fl(q)=Nl(q)f(q)

(20)

并将其在奇异点p附近展开为Taylor级数,即

(21)

其中:

图7 裂纹单元超奇异积分计算
Fig.7Hypersingular integral calculation of crack element

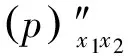
(22)

(23)

将式(21)代入式(19)，将式(19)表示为两个积分之和

Il=I0+I

(24)

其中:

(25)

(26)

因此，式(19)的积分等价于式(25)和式(26)表示的两个积分。

对于积分I0，由式(23)可知，由于ΔFlp,q=OR3而使被积函数的奇异性消除，因此可直接利用Gauss求积公式计算。

I=2μA·

(27)

由式(27)可见，为了计算I值，只需研究有限部分积分

(28)

其中k1和k2的取值为：k1=k2=0;k1=k2=1;k1=2,k2=0;k1=0,k2=2。

如图7所示，令

x1-ξ1=rcosθ

x2-ξ2=rsinθ

则

(29)

这样就将二维的有限部分积分化为一维的有限部分积分。将式(22)代入式(29)，对r积分并取有限部分，得

(30)

其中:

(31)

式(31)中的被积函数已无奇异性，可用数值积分进行计算。为了便于利用Gauss求积分式计算，将积分变量再作如下变换。

设单元Sk的周边由M条简单曲线段所组成，如图7所示，将式(30)对θ的积分变换为对描述单元周边各曲线段的广义坐标γ的积分。对于单元周边第m条曲线段，有

(32)

Jm可由式(31)和式(32)导出,即

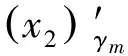
(33)

将式(32)和式(33)代入(30)，得到

(34)

对于(部分)椭圆，将其映射到(部分)单位圆上划分单元，映射关系为

(35)

椭圆裂纹及单位圆上的单元划分如图8所示。

由式(35)，可以方便地导出式(33)的Jm。

(36)

J1

(37)

(38)

(39)

图8 椭圆裂纹及单位圆上的单元划分
Fig.8Elliptical crack and element division of unit circle

由于式(36)和式(38)分别表示以φ和ρ为参数的双曲线族和椭圆族，故将图8(a)所示单元称为双曲线-椭圆单元。

求解式(14)和式(15)，得到基本线性代数方程组:

(40)

由此得到裂纹前缘周边任意D点(见图4)所在单元的权函数Wj(D)j=z,n,t,进而确定D点的应力强度因子为

(41)

式中：E为弹性模量。对于(部分)椭圆裂纹(见图5)。

1.3 疲劳裂纹扩展和寿命分析方法

工程中计算疲劳裂纹扩展的一般形式的方程为

(42)

式中：αi(i=1,2,…,m)为材料常数和环境及其他力学量。其中最常用的是Paris公式(见式(43),对于表面裂纹的表面点，一般认为其闭合效应与裂纹最深点不同，通常采用ΔKeff=0.9ΔK代替式(43)中的ΔK，本文也采用该方法)。

(43)

或

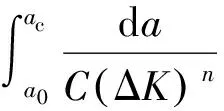
(44)

式中：a0和ac分别为初始和终止裂纹深度。

由式(41)、式(43)和式(44)可知，要高效和精确计算表面裂纹疲劳扩展，需要解决两个关键问题：① 每一个裂纹扩展步下，由于需要计算当前的应力强度因子(幅)，因此对应于每一个扩展步，单元网格的自动生成;② 由于式(40)左边为大型、满秩、非对称矩阵，计算矩阵系数和求解式(40)需要耗费大量的时间，计算效率很低。

本文通过以下技术解决以上两个关键问题，从而实现表面疲劳裂纹扩展的高效高精度计算。

1) 通过适当的排列，使得形成的线性代数方程组具有以下形式：

(45)

式中：A0为主控矩阵，其只与边界Γ的几何形状和边界条件有关(即式(14)右边的前2个积分)，而与裂纹扩展无关，故只需在初始裂纹状态下计算一次，在随后的疲劳裂纹扩展过程中，无需再重复计算，而只需计算矩阵B1、B2和C，而这3个矩阵占整个矩阵的计算量为

式中：NC和N0分别为裂纹单元节点数和非裂纹单元节点数，对于一般的表面裂纹问题，NC<100(本文研究中取NC=88)，而对于一般的实际工程构件，N0一般为几千到几万，故每一个疲劳裂纹扩展步下的矩阵计算量约比初始裂纹状态下的矩阵计算量小1～2个量级。

2) 通过矩阵运算，求得式(45)左边系数矩阵的逆矩阵为

(46)

其中:

由此可以求得式(45)的解为

(47)

由于在疲劳裂纹扩展过程的每个步中，只需要计算当前裂纹的应力强度因子(式(47)中对应的未知量U)，故式(47)还可以进一步简化为

(48)

式中：A0只需要在裂纹初始状态下计算一次，随后的每次疲劳裂纹扩展，只需计算B1、B2和C，又由于式(48)给出了U的显式解，无需求解大型线性代数方程组，大大提高了计算效率。

3) 对于工程中的疲劳裂纹，例如最常见的半椭圆表面裂纹、拐角1/4椭圆表面裂纹等，将它们均映射到(部分)单位圆上划分单元(见图8)。疲劳裂纹扩展中虽然裂纹尺寸a、b发生变化，但单位圆上的单元始终不变，因此疲劳扩展过程中，通过映射关系式(35)，实际物理平面上的单元自动调整(自动重新划分)。

由于针对每一个新的裂纹扩展步，重新精确计算(数值意义上)当前应力强度因子，所以是一种高精度的疲劳裂纹扩展计算方法；而对于每一个新的裂纹扩展步，计算工作量只是第一次计算的1/10～1/100左右，效率高，且整个计算只需一次输入初始参数，随后全部自动完成。

2 算例与试验考核

2.1 算 例

算例主要考核混合边界元法计算应力强度因子的精度。图9(a)所示远场受均匀拉伸应力σ作用的板内半椭圆表面裂纹，几何尺寸为：a/w=a/h=0.2。裂纹面上单元划分为Nφ×Nρ=11×4=44，b/a=0.2与b/a=1.0的计算结果与Raju和Newman, Jr[2]利用三维有限元法用了近万个自由度在大型计算机上求得结果进行比较，如图9(a)和图9(b)所示，图中Φ为第二类椭圆积分。由图9可知，两者结果吻合很好。

算例表明，本文所建立的混合边界元法是可靠的，用于计算表面裂纹应力强度因子与有限元等方法具有同等的精度。

图9平板半椭圆表面裂纹受均匀拉伸应力时的 应力强度因子
Fig.9 Stress intensity factor of semi-elliptical surface crack in plate subjected to uniform tensile stress

2.2 表面裂纹疲劳扩展试验考核

为了说明混合边界元法计算疲劳裂纹扩展的高效和高精度，进行试验考核。

试样为图9(a)所示远场受拉伸应力σ的平板半椭圆表面裂纹试样，材料为16Mn钢，几何尺寸为w×t×h=38 mm×10 mm×120 mm、初始裂纹尺寸和应力幅如表1所示。初始裂纹通过厚度为0.13 mm的砂轮加工而成，共3个试样。

试验在Instron试验系统上进行，试验过程中“降载留痕”，试验结束后，打开断口，进行高温氧化，通过“降载留痕+氧化着色”可以清晰地看到断口上的“Beachmark”，由此测得疲劳裂纹扩展量与循环次数的关系。

将3个试样的试验结果用Paris公式(见式(43))进行疲劳裂纹扩展速率计算(回归分析)，得到16Mn钢Paris公式材料常数为：C=4.41×10-8，n=3.61。数值分析中，利用对称性，取1/4几何模型，模型表面单元划分和边界约束如图10所示，表面节点数和单元数分别为1 185和372(通常边界ΓⅠ上的单元有357个，边界ΓⅡ上非协调单元有15个)，裂纹面上单元数为Nφ×Nρ=11×4=44。

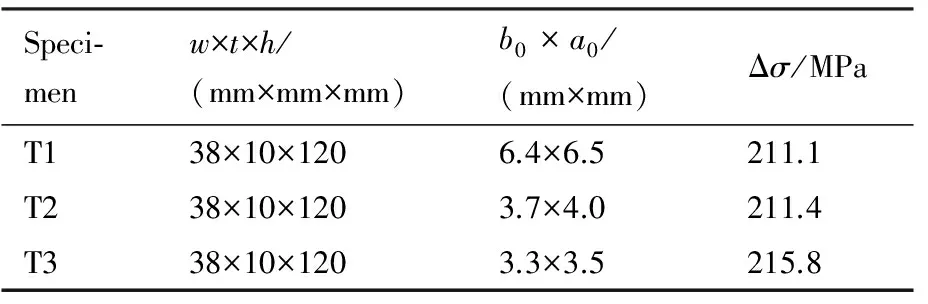
表1 试样几何尺寸、初始裂纹尺寸与压力幅

图10 数值分析模型
Fig.10 Numerical analysis model

疲劳裂纹扩展及应力强度因子的计算结果与试验结果如图11所示。由图11可见，计算结果与试验结果非常一致。

图11 表面裂纹疲劳扩展数值分析与试验结果的比较
Fig.11Comparison of numerical analysis and test results of fatigue growth of surface crack

3 结 论

1) 建立的混合边界元法基本方程和数值求解技术基于精确的弹性力学理论和数学方法，因此是一种严格可靠的数值分析方法，可用于计算任意三维裂纹应力强度因子和基于线弹性断裂力学的疲劳裂纹扩展分析，数值算例表明，混合边界元法与有限元法具有同等级别的精度。

2) 混合边界元法用于表面裂纹疲劳扩展计算，对于每个裂纹扩展步均能精确(数值意义)计算应力强度因子，因此这是一种高精度计算表面裂纹疲劳扩展的方法。

3) 除了在初始裂纹状态下需要计算大型非对称系数矩阵外，对于随后的疲劳裂纹扩展，只需做小规模矩阵的计算(结构越大，这种优势越明显)，且以显式形式给出应力强度因子解而无需求解大型线性代数方程组，大大提高了计算效率。

4) 疲劳裂纹扩展过程中，单元需要不断重新划分，由于混合边界元法中的主控矩阵与裂纹无关，故只需对裂纹表面单元进行重新划分，对半椭圆表面裂纹，由于单位半圆上单元在疲劳扩展过程中不变，从而通过映射关系自动重新划分裂纹表面单元。

综上所述，混合边界元法用于表面裂纹疲劳扩展计算，只需一次输入初始数据即可进行全疲劳过程的高效和高精度自动分析。本文的研究为工程结构表面裂纹疲劳扩展和寿命计算的高效高精度数值分析建立了理论基础和实现方法。

[1] 胡博, 于润桥, 徐伟津. 人工槽模拟GH4169涡轮盘表面裂纹缺陷的微磁检测[J]. 航空学报, 2015, 36(10): 3450-3456.

HU B, YU R Q, XU W J. Micro-magnetic NDT for surface crack defect in a GH4169 turbine disc simulated by artificial groove[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3450-3456 (in Chinese).

[2] RAJU I S, NEWMAN J C, Jr. Stress-intensity factors for a wide range of semi-elliptical surface cracks in a finite-thickness plate[J]. Engineering Fracture Mechanics, 1979, 11(4): 817-829.

[3] 国家标准化管理委员会. 在用含缺陷压力容器安全评定: GB/T 19624—2004[S]. 北京: 中国标准出版社, 2004.

Standardization Administration of China. Safety assessment for in-service pressure vessels containing defects: GB/T 19624—2004[S]. Beijing: China Standard Press, 2004 (in Chinese).

[4] LIN X B, SMITH R A. Finite element modelling of fatigue crack growth of surface cracked plates: Part I: The numerical technique[J]. Engineering Fracture Mechanics, 1999, 63(5): 503-522.

[5] LIN X B, SMITH R A. Finite element modelling of fatigue crack growth of surface cracked plates: Part II: Crack shape change[J]. Engineering Fracture Mechanics, 1999, 63(5): 523-540.

[6] LIU C H, CHU S K. Prediction of shape change of corner crack by fatigue crack growth circles[J]. International Journal of Fatigue, 2015, 75: 80-88.

[7] YU P S, GUO W L. An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution[J]. Engineering Fracture Mechanics, 2012, 93: 65-74.

[8] GUCHINSKY R, PETINOV S. Numerical modeling of the surface fatigue crack propagation including the closure effect[J]. International Journal for Computational Methods in Engineering Science and Mechanics, 2016, 17(1): 1-6.

[9] 李有堂, 张洋洋. 压力容器中表面裂纹在高周疲劳下的扩展规律[J]. 兰州理工大学学报, 2015, 41(6): 168-172.

LI Y T, ZHANG Y Y. Surface crack growth pattern of pressure vessel with high-cycle fatigue[J]. Journal of Lanzhou University of Technology, 2015, 41(6): 168-172 (in Chinese).

[10] CHAI G Z, FANG Z M, JIANG X F, et al. Hybrid boundary element analysis for surface cracks[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(23-26): 2069-2086.

[11] WATSON J O. Advanced implementation of the boundary element method for two and three-dimensional elastostatics[J]. Developments in Boundary Element Methods, 1979, 61: 31-63.

[12] IOAKIMIDIS N I. Application of finite-part integrals to the singular integral equations of crack problems in plane and three-dimensional elasticity[J]. Acta Mechanica, 1982, 45(1-2): 31-47.

Ahighlyefficientandaccuratenumericalanalysismethodforfatiguepropagationofsurfacecrackandlifeprediction

CHAIGuozhong1,*,LYUJun1, 2,BAOYumei1,JIANGXianfeng1,DINGHao1

1.CollegeofMechanicalEngineering,ZhejiangUniversityofTechnology,Hangzhou310012,China2.SchoolofMechatronics&IT,YiwuIndustrial&CommercialCollege,Yiwu322000,China

Thebasictheoryandnumericalsolvingtechniqueofthehybridboundaryelementmethodforthecalculationofthestressintensityfactorsofthree-dimensionalcrackisestablishedbasedonthetheoryofelasticmechanics.Inanalyzingthefatiguepropagationofthesurfacecrack,thestressintensityfactorateachcrackpropagatingstepneedstobecalculated,andaccordinglythelargenon-symmetriccoefficientmatrixshouldbecomputedrepeatedly.Amethodisproposedthatthemastermatrixiscalculatedonlyonceintheinitialcrackstate,andthenaverysmall-scalematrixiscalculatedduringthesubsequentfatiguecrackpropagation.Thesolutionforthestressintensityfactorisalsogiveninanexplicitformwithoutsolvinglarge-scalelinearalgebraicequationssothatthecalculationefficiencyisimprovedgreatly.Toaddresstheproblemofcontinuousdivisionandremeshingofelementsduringthefatiguecrackpropagating,thehybridboundaryelementmethodisappliedasthemastermatrixisindependentofthecrack,andthereforeonlyremeshingofelementsonthecracksurfaceisrequired.Forthesemiellipticalsurfacecrack,theelementsonthecracksurfaceareremeshedaccordingtothemappingrelationshipasthecrackismappedintothesemicircleinmeshingandtheelementsintheunitsemicirclehavenochangeduringthefatiguepropagation.Theaccuracyandreliabilityoftheproposedmethodareverifiedbyseveralexamplesandexperiments.Theresearcheffortsmayprovidethetheoreticalfoundationandtherealizationmethodforhighlyefficientandaccuratenumericalanalysisofthesurfacecrackfatiguepropagationandthelifepredictionofengineeringstructures.

surfacecrack；fatiguepropagation；highlyefficientandaccurateanalysis；hybridboundaryelementmethod；stressintensityfactor

2017-03-29；

2017-04-06；

2017-04-10；Publishedonline2017-04-261801

URL：http://hkxb.buaa.edu.cn/CN/html/20171217.html

NationalNaturalScienceFoundationofChina(51275471)

.E-mailchaigz@zjut.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221291

2017-03-29；退修日期2017-04-06；录用日期2017-04-10；网络出版时间2017-04-261801

http://hkxb.buaa.edu.cn/CN/html/20171217.html

国家自然科学基金(51275471)

.E-mailchaigz@zjut.edu.cn

柴国钟,吕君,鲍雨梅，等. 表面裂纹疲劳扩展和寿命计算的高效高精度数值分析方法J. 航空学报，2017,38(12):221291.CAIGZ,LYUJ,BAOYM,etal.AhighlyefficientandaccuratenumericalanalysismethodforfatiguepropagationofsurfacecrackandlifepredictionJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):221291.

V215.5+5

A

1000-6893(2017)12-221291-12

徐晓)