非平整曲面隔震结构的双自由度动力模型及地震响应研究

孙实 刘文光 田坤

摘要： 针对强地震作用下隔震结构隔震层变形过大的现象提出了曲面隔震结构体系，该结构隔震层为曲面布置，在地震作用和结构重力作用下上部结构可绕曲率中心进行曲面运动。建立了非平整曲面隔震结构双自由度动力分析模型，通过数值分析进一步研究非平整曲面隔震层的曲率半径对结构地震响应、受力特性的影响规律，确定非平整隔震层的合理曲率半径。采用钢框架模型结构进行了曲面隔震结构的地震模拟振动台试验，试验結果表明，非平整曲面隔震结构相比于普通隔震结构，上部结构加速度平均放大幅度略有增大，曲面隔震支座具有良好的滞回耗能能力，实现了隔震层位移响应和上部结构位移响应的有效控制。

关键词： 曲面隔震结构； 地震响应； 振动台试验； 双自由度； 曲率半径

中图分类号： TU352.12； TU317+.2 文献标志码： A 文章编号： 1004-4523（2018）05-0780-09

DOI：10.16385/j.cnki.issn.1004-4523.2018.05.007

1 概 述

随着高层建筑的兴建及隔震技术的发展，隔震技术为避免或减轻高层建筑强震损伤破坏提供了一条有效途径[1-3]。经过多年来学者的研究和应用，在高层隔震结构计算理论和分析方法、减震机理等方面取得显著的成果。但在强震作用下，高层隔震结构会由于侧向水平位移过大，引起与相邻构造物碰撞，影响结构整体稳定。Nagarajaiah等[4-5]介绍了在Northridge地震中基础隔震结构发生碰撞的情况。因此进行强震下隔震结构限位研究是十分重要的。

为此，刘文光等[6-7]建立考虑扭转影响的多质点体系计算模型，并进行大高宽比隔震结构振动台试验，着重研究了隔震的基本原理。Matsagar和Jangid[8]研究隔震类型、上部结构自振周期和附加刚度对基础隔震结构碰撞反应的影响。韩淼等[9-10]提出了大震作用下隔震层软碰撞限位方案，设置软碰撞限位装置，当隔震层位移达到预留距离时，限位装置通过软碰撞将隔震层位移限制在允许范围内。赵亚敏等[11]构思了一种剪切耗能型隔震层限位装置，通过弹性防撞阻尼材料和限位挡板来提高基础隔震体系在近断层地震作用下的安全性。这些研究主要是从结构布置合理性、采用附加耗能碰撞装置进行隔震层限位，所需的代价和成本较高。

研究人员提出采用新型的隔震结构运动模式的新思路。P S Harvey和George C Lee[12-13]提出滚动隔震体系（Rolling Isolation System），该结构可以通过圆柱体滚棒在滑动面上滚动实现水平隔震，通过摩擦进行耗能，同时利用重力作用实现结构的自复位能力。Yutaka Nakamura等[14]指出在日本采用核心悬挂隔震的建筑物已用于工程实践，在核心筒上设置“帽型”桁架和双层倾斜隔震支座延长自振周期。以上的共同特点是其隔震层运动形态都是曲面，利用结构自重和隔震支座实现结构隔震效果。

本文提出曲面隔震结构，如图1所示。该结构区别于传统平面隔震结构，在无地震作用时隔震层顶板保持平整状态，在强地震作用下，隔震层及上部结构的运动轨迹是曲面。本文通过提出该体系的动力计算模型，对其进行参数分析研究，在此基础上通过振动台试验对相关结论进行验证。

2 曲面隔震双自由度动力分析模型

2.1 曲面隔震双自由度模型的建立 在普通隔震结构中，通常将上部结构近似看成刚体，结构做剪切型运动，结构的变形以隔震层的平动为主。本文提出的曲面隔震结构，上部结构整体绕隔震层形成的曲率中心做摆动。

将曲面隔震体系进行简化分析，隔震层由两个倾斜的橡胶支座构成，其轴向延长线的交点O为曲面隔震体系的转动中心，曲率半径为R；上部结构和隔震层的质量m集中于结构的质心处，其高度为h，并通过无质量的刚性杆与隔震层相连，d为质点与转动中心O点的距离。结构对质心的转动惯量为IG，对曲率中心的转动惯量为J；结构宽度为B，高度为H；曲面隔震层的等效侧向刚度为k，阻尼系数为c，且单个竖向刚度采用拉压等刚度为kv，竖向阻尼系数为cv。

2.2 曲面隔震双自由度模型的动力方程

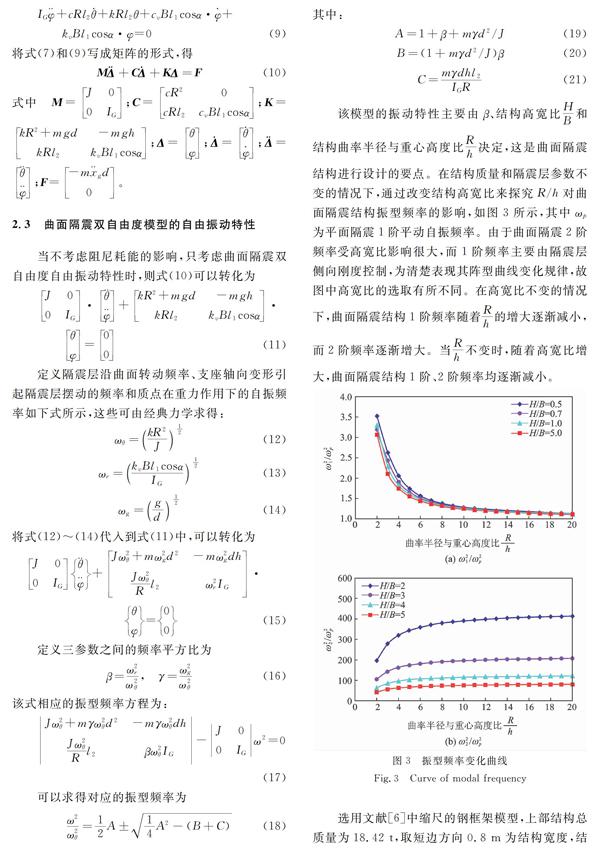
该模型的振动特性主要由β、结构高宽比HB和结构曲率半径与重心高度比Rh决定，这是曲面隔震结构进行设计的要点。在结构质量和隔震层参数不变的情况下，通过改变结构高宽比来探究R/h对曲面隔震结构振型频率的影响，如图3所示，其中ωp为平面隔震1阶平动自振频率。由于曲面隔震2阶频率受高宽比影响很大，而1阶频率主要由隔震层侧向刚度控制，为清楚表现其阵型曲线变化规律，故图中高宽比的选取有所不同。在高宽比不变的情况下，曲面隔震结构1阶频率随着Rh的增大逐渐减小，而2阶频率逐渐增大。当Rh不变时，随着高宽比增大，曲面隔震结构1阶、2阶频率均逐渐减小。

选用文献[6]中缩尺的钢框架模型，上部结构总质量为18.42 t，取短边方向0.8 m为结构宽度，结构总高度为4 m。隔震层侧向刚度取值区间为1.2～2.4 kN/mm，侧向刚度对曲面隔震频率的影响如图4所示。

3 曲面隔震结构的数值分析

3.1 分析模型参数选取 将2.3节中所述上部结构作为分析模型。在钢框架的四个柱脚分别布置LRB100-G6型支座，支座屈服后刚度为0.26 kN/mm，采用橡胶层厚度50%剪切变形对应的等效刚度为0.467 kN/mm，等效阻尼比为0.283。则隔震后周期为0.835 s（按屈服后刚度算），支座详细参数见表1。

按抗震规范选取符合设计反应谱的3条实测地震动，1952年美国加利福尼亚地震时的Taft波、1995年神户地震时的Hachinohe波及1999年中国台湾南投地震时的Chi-Chi波。图5为经调幅后的3条地震波反应谱与八度多遇地震下的标准反应谱对比。

3.2 时程分析

3.2.1 结构响应

时程分析选用上述三条地震动，地震波输入峰值为0.2g。曲面隔震结构模型在不同曲率半径下结构响应会有差异，分别选取5h，10h及平面三种曲率半径进行比较。当曲率半径接近无穷大时，曲面隔震结构转化为传统的平面隔震。表2和3分别为在不同曲率半径下，质点加速度和位移响应的对比。当Rh=5时，加速度响应偏差率最大为23.3%，位移響应偏差率最大为-23.7%。图6为激励峰值为0.2g时不同地震波作用下，Rh=5的曲面隔震与平面隔震缩尺模型对应到原型结构的加速度时程对比。

3.2.2 隔震层滞回性能

隔震层的滞回性能反映隔震支座吸收地震能量并减少上部结构的地震响应的能力。图7和8为0.2g激励峰值下曲面与平面隔震的滞回曲线对比图。由图可以看出，曲面隔震滞回曲线整体倾斜程度较平面隔震要大，这是因为当曲率半径较小时，重力效应对结构影响较大，公式（10）中重力项增加结构整体的刚度。曲面隔震在地震作用下滞回曲线饱满，耗能能力较强。曲率半径的不同对结构响应和隔震层滞回性能影响很大。

3.3 模型合理曲率半径的选取

通过探究曲面隔震地震响应及支座竖向力峰值变化规律确定合理曲率半径的选取。以模型短边方向为结构宽度，曲率半径选为3h，4h，5h，…，100h及平面。加速度放大率为曲面隔震质点加速度与平面隔震质点加速度之比，位移减小率为曲面隔震质点相对位移与平面隔震质点相对位移之比。

图9为地震加速度峰值为0.4g时，质点响应变化率、支座竖向力最大值与Rh的关系。图中未给出32h后的数据是因为曲率半径大于32h时结构响应变化不明显。从图中可以看出不同的地震激励下结构响应差别很大，结构加速度放大率随Rh的增大而逐渐减小。而位移减小率随Rh的增大而逐渐增大，表明可以通过减小曲率半径的方式，达到结构限位的目标。当放大率与减小率之差小于0.1时，即Rh值大于20时，结构响应逐渐趋于稳定。

在Chi-Chi波作用下，支座竖向力最大值呈先减小后增大，最后逐渐稳定的趋势，Rh值为8时为趋势的拐点。Taft波呈现出与Chi-Chi波类似的趋势。在Ha波激励下，支座竖向力最大值在Rh大于14后逐渐减小。结合结构响应变化率确定模型的合理曲率半径区间为8h～10h时，大震时可控制结构水平位移和特定地震输入下支座的拉应力，同时在合理范围内，允许隔震结构出现加速度适量放大。

4 曲面隔震体系振动台试验

4.1 试验概况 振动台上部结构为5层钢框架，模型与原模型结构的相似比为112。模型每层的层高为0.98 m，X向为一跨，其纵向长度为0.81 m；Y向为两跨，横向长度为1.62 m，模型总高度为4.9 m，模型总质量为13 t，图10为曲面隔震结构试验模型。采用具有非平整隔震层的曲面隔震体系。试验选取两种曲率半径，分别为13 m（5倍结构重心高度）和平面。试验中支座为LRB100型，选用El Centro波和Taft波作为地震动输入。曲面隔震层布置见图11。

4.2 试验结果分析

输入地震动工况两种隔震结构的加速度响应对比。El波、Taft波作用下曲面隔震结构水平向各层的加速度放大率均大于平面隔震相对应值。El Centro波输入下，X向曲面隔震结构放大幅度为8%～18%，平均值为9%，Y向放大幅度平均为20%。Taft波作用下，水平向平均放大幅度分别为26%和18%。由于高宽比较大，El Centro波下加速度分布形式呈现出两端反应大，中间层反应较小的折线状。

比较峰值加速度为0.3g，且三向地震作用下的两种结构的各层相对台面位移幅值，如图13所示。El Centro波输入下，曲面隔震结构各层相对台面位移幅值均小于平面隔震对应值，X向和Y向平均位移减小幅度分别为24.1%和22.6%。Taft波输入下，上部结构平均位移减小幅度为17.1%，顶层减小幅度最大为33.2%，隔震层位移也明显减小。曲面隔震结构可显著减小结构位移，达到限位目标。

图14为输入峰值0.3g三向地震波激励下，支座Y向滞回曲线。El Centro波输入下，曲面隔震支座的滞回环较平面隔震饱满，铅芯橡胶支座起到了滞回耗能的作用。El Centro波和Taft波下，曲面隔震层水平位移减小幅度分别为15.6%和10.1%。

5 结 论

本文提出新型的具有非平整隔震层的曲面隔震体系，并建立其简化分析模型及双自由度动力方程，针对振动台试验模型进行地震响应分析及参数影响研究，得出以下结论：

（1） 结构高宽比、曲率半径与重心高度比影响曲面隔震结构的动力特性。当高宽比不变时，曲面隔震结构一阶频率随着Rh的增大而逐渐减小，二阶频率逐渐增大。当Rh不变时，随着高宽比增大，曲面隔震结构一阶、二阶频率均逐渐减小。

（2） 选用三条强震记录对振动台试验模型进行数值分析。针对三种曲率半径分析，加速度响应偏差率最大为23.3%，位移响应偏差率最大为-23.7%。

（3） 通过对加速度放大率、位移减小率和支座竖向力最大值的分析，得出模型合理曲率半径。当曲率半径为8～10倍于重心高度时，可有效控制结构水平位移和在特定地震作用下的支座拉应力。

（4） 对曲面隔震结构进行缩尺振动台试验，相比于平面隔震结构，曲面隔震结构的加速度平均放大幅度为9%～26%。上部结构位移显著减小，顶层位移减小幅度最大为33.2%，隔震层水平位移得到有效控制。同时曲面隔震支座具有良好的滞回耗能能力。

参考文献：

[1] 朱玉华， 吕西林， 施卫星， 等. 铅芯橡胶基础隔震房屋模型地震反应分析[J]. 振动工程学报， 2003，16（2）：256—260.

Zhu Yuhua， Lu Xilin， Shi Weixing， et al. Analysis of the seismic response of the building models with lead rubber bearings for vibration isolation[J]. Journal of Vibration Engineering， 2003，16（2）：256—260.

[2] Chung W J， Yun C B， Kim N S， et al. Shaking table and pseudodynamic tests for the evaluation of the seismic performance of base-isolated structures[J]. Engineering Structures， 1999，21（4）：365—379.

[3] Komuro T， Nishikawa Y， Kimura Y， et al. Development and realization of base isolation system for high-Rise buildings[J]. Journal of Advanced Concrete Technology， 2005，3（2）：233—239.

[4] Nagarajaiah S， Sun X. Base isolated FCC building： impact response in Northridge earthquake[J]. Journal of Structural Engineering， 2001，127（9）：1063—1075.

[5] Nagarajaiah S， Sun X H. Response of base-isolated USC hospital building in Northridge earthquake[J]. Journal of Structural Engineering， 2000，126（10）：1177—1186.

[6] 刘文光.橡胶隔震支座力学性能及隔震结构地震反应分析研究[D]. 北京：北京工业大学， 2003.

Liu Wenguang. Mechanics properties of rubber bearings and earthquake response analysis of isolated structure [D]. Beijing： Beijing University of Technology， 2003.

[7] 劉文光， 闫维明， 霍 达， 等. 塔型隔震结构多质点体系计算模型及振动台试验研究[J]. 土木工程学报， 2003， 36（5）： 64—70.

Liu Wenguang， Yan Weiming， Huo Da， et al. Computation model and shaking table test for isolated MDOF tower structure [J]. China Civil Engineering Journal， 2003， 36（5）： 64—70.

[8] Matsagar V A， Jangid R S. Seismic response of base-isolated structures during impact with adjacent structures[J]. Engineering Structures， 2003，25（10）：1311—1323.

[9] 韩 淼， 周锡元. 基础隔震建筑软碰撞保护分析[J]. 建筑科学， 1999， 15（1）：14—20.

Han Miao， Zhou Xiyuan. Analysis of soft collision protection of base isolated building [J]. Building Science， 1999，15（1）：14—20.

[10] 韩 淼， 沙千里， 温增平. 近断层区橡胶支座隔震结构限位研究[J]. 世界地震工程， 2013，29（1）：74—79.

Han Miao， Sha Qianli， Wen Zengping， et al. Study on displacement limit of rubber bearing isolation buildings in near-fault region[J]. World Earthquake Engineering， 2013，29（1）：74—79.

[11] 赵亚敏，陆 鸣，喻 烟.一种剪切耗能型隔震层限位装置： CN203716324U[P]. 2014.

Zhao Yamin， Lu Ming， Yu Yan. A shear dissipation device to limit displacement in isolation layer： CN203716324U [P]. 2014.

[12] Harvey P S. Vertical accelerations in rolling isolation systems： Experiments and Simulations [J]. Journal of Engineering Mechanics， 2016，142（3）：04015091.

[13] Lee G C， Ou Y C， Niu T， et al. Characterization of a roller seismic isolation bearing with supplemental energy dissipation for highway bridges [J]. Journal of Structural Engineering， 2010，136（5）：502—510.

[14] Nakamura Y， Saruta M， Nakanishi T， et al. Development of the core-suspended isolation system [C]. The World Conference on Earthquake Engineering， Beijing， China， 2008.

[15] Pan T C， Kelly J M. Seismic response of base-isolated structures with vertical-rocking coupling[J]. Earthquake Engineering & Structural Dynamics， 2010，12（5）：681—702.

[16] Perotti F， Domaneschi M， Grandis S D. The numerical computation of seismic fragility of base-isolated nuclear power plants buildings[J]. Nuclear Engineering & Design， 2013，262：189—200.

Abstract： The deformation of isolation layer subjected to strong earthquake action is often excessively large. For this reason， the curved-surface isolated structural system is proposed， in which the isolation layer is uneven. In the curved-surface isolated building， the superstructure is able to pivot freely around the center of curvature due to the seismic and gravity effect. In this paper， a two-degree-of-freedom dynamic equation of the system is established first， and then the relationship between the curvature radius and the seismic response， mechanical behavior of the structure are studied through numerical analysis. Based on this study， the optimal curvature radius of the uneven isolation layer is determined. After that， a shake table test of the curved-surface isolated structure is performed using five-storey steel frame model. The results show that the average acceleration amplification factor of superstructure increases slightly compared to the conventional isolated structures. Meanwhile， a favorable energy dissipation capacity is observed for the isolator of the curved-surface isolated structure. Specifically， the displacement response of the isolation layer and the superstructure was effectively controlled.

Key words： curved-surface isolated structure； seismic response； shake table test； two-degree-of-freedom； curvature radius

作者簡介： 孙 实（1993—），男，硕士研究生。电话： 18800200852； E-mail：sunshi@i.shu.edu.cn

通讯作者： 刘文光（1968—），男，工学博士，教授。电话： （021）66135129； E-mail：liuwg@aliyun.com