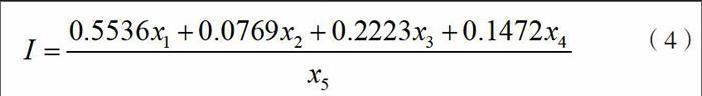分配教育投资的优化策略

院旺

[摘要]本文研究了在已知教育投资金额和候选学校的情况下，应选取哪些学校作为投资对象，并如何计算出每个学校应该分配的金额。本文采取数据处理、建模分析兩步走的整体思路进行分析，进而得出结果。

[关键词]教育投资；层次分析法；投资回报率

doi：10.3969/j.issn.1673-0194.2017.18.074

[中图分类号]G526.7 [文献标识码]A [文章编号]1673-0194（2017）18-0120-02

1问题说明

从2016年7月起，Goodga-ant基金会计划每年向合适的学校捐赠1亿美元，为期五年。现在本文要建立一个投资策略，旨在让投资者得到最优的社会回报。

对于这个问题，本文会给出投资学校的数量、投资学校的名单以及每所学校的投资金额。同时，本文将给出这笔捐款的社会回报指标的计算方法，然后指导未来的融资过程。

2数据分析

2.1层次分析法

层次分析法（简称AHP）是一种有效的多目标决策方法，将定性分析与定量分析相结合。该方法通过对数学方法中的所有级别进行排序，计算出反映各级相对重要性的元素的权重以及所有元素的相对权重，然后给出问题的最终决定

2.2无量化法

本文采用的无量化方法有平均值归一化方法和最大差异归一化方法。

2.2.1平均值归一化方法

该方法获取与每个元素对应的数据平均值，结果是每个元素的数据除以数据的平均值。公式如下：

2.3投资回报率的计算

投资回报率（ROI）是投资者因投资某些资源而受益。高投资回报率意味着投资收益与投资成本相当。单期回报率是收益（净利润）除以所投入的资源（金额）所得的值。

3建模分析

3.1将一些不符合硬性条件的学校从候选名单中剔除

这一步应视不同的情况采取不同的策略，如没有全日制学生的学校不予考虑等。

3.2元素的分割和数据的无量纲化

本文将人口数据分为6类，即财务能力、还款能力、毕业率、考试成绩、其他组织的捐赠和大学人口将数据。在分析某一类别时，本文选择一个因素作为主要因素，并分析其他因素与主要因素之间的相关性。然后，本文将具有强相关性的因素分为一类，然后进行无量化，无量化的方式采用平均值归一化方法和最大差异归一化方法。

3.3根据基础需要对大学进行排序

接下来，本文确定投资指标与五个因素之间的关系。根据实际情况，本文确定投资指标和财务能力、还款能力、毕业率、考试成绩呈正相关，其他组织的捐赠呈负相关，公式如下：

本文根据公式（4）计算每一个学校的投资需求指数，然后根据该指数对学校进行排序。

3.4确定投资分配的权重

假设某组织决定捐钱给N所大学，该组织该如何分配钱？假设有两所大学名为A和B，如果A的需求超过B的需求，组织应该把更多的钱投入A。但是，如果A的需求与B的需求一样多，但是B的学生人数较多，那么组织应该投资更多的钱给B.

经过上述分析，组织决定使用非尺寸资金需求指数乘以大学生人数，结果是投资分配的权重

3.5计算投资回报率以确定选取学校的数量

接下来，本文考虑如何确定大学数量。笔者分别计算出投资一个学校、投资两个学校、投资所有学校的投资回报率，并选取ROI最高的作为结果。

投资回报率和什么有关呢？首先是投资金额，其次是大学毕业后的平均工资，最后是大学的数量，得到下式：

那么，投资N所学校得到的总投资回报率为：最大值，换句话说，投资的学校数量应该是156。

4计算结果

本文将从候选的学校中选取156所学校进行投资，金额从多到少排序，排名前10位的学校如表1所示。