基于听觉原理的谐波频率自动提取方法
李允公, 叶利丽, 郑国威, 毛怒涛, 应远军
(1.东北大学机械工程与自动化学院 沈阳,110819)(2.松下家电研究开发(杭州)有限公司 杭州,310018)
基于听觉原理的谐波频率自动提取方法
李允公1, 叶利丽1, 郑国威2, 毛怒涛2, 应远军2
(1.东北大学机械工程与自动化学院 沈阳,110819)(2.松下家电研究开发(杭州)有限公司 杭州,310018)
基于听觉系统的运行机制,提出一种可自动识别和提取信号中谐波频率的计算方法。首先,对信号进行基底膜带通滤波;其次,模拟听皮层时频感受野现象对不同时频域内信号进行二维傅里叶变换并提取幅值和频率信息,基于幅值信息的侧抑制结果,提出了一种谐波成分频率点的判据方法;最后,对提取得到的谐波频率点进行重组,从而可揭示信号中的主要频率成分以及各成分的时变情况。数值仿真和试验数据验证结果表明,所提方法可准确提取信号中的各谐波频率,并具有一定的抗噪声干扰能力,对于微弱谐波成分的频率提取亦有较好效果。
听觉模型;频率提取;带通滤波;侧抑制;故障诊断
引 言
在设备故障诊断中,通常需明确振动信号所包含的主要频率分量及其时变情况,有时信号的频率结构比幅值信息更为重要[1-2]。实际中常遇到的一个问题是,当信号结构较为复杂、谐波分量幅值微弱、存在随机噪声干扰或缺少必要的辅助信息时(如键相位或编码器信号),除了频谱中幅值突出的离散谱线之外,仅通过人为观察往往难以准确判断频谱中哪些谱线对应谐波成分及哪些谱线对应随机噪声,虽然结合时频谱图可提高判断的准确性,但仍可能遗漏幅值微弱的频率成分。同时,对于信号数据量过大或现场连续监测的场合,则需由计算机对每一频率成分的性质进行自动判断。因此,有必要研究一种能够自动识别、提取与跟踪谐波频率成分的信号分析方法。
目前,在缺少键相位信号或设备参数等辅助信息时,人工的信号分析思路多是搜索频谱中幅值较高的谱线所对应的频率值;进而寻找倍频及边频值;若进行自动识别,则多是基于图像处理的方法从时频谱图中提取频率值等信号特征[3-5]。显然,当存在噪声干扰和谐波幅值微弱时,两类方法均难以获得良好的效果,且均未充分利用信号的内部信息。
人类听觉系统可有效区分不同频率和不同频率结构的声音,并能够跟踪同一声源的时变频率[6]。同时,在从外耳至听觉中枢这一完整的信息处理通道上,频率始终是一个的重要参量而被不断使用[7]。例如,听觉皮层中不同的神经元具有不同的时频感受野[8],即只对特定的频率成分产生最大的响应,从而可实现频率的识别和提取。因此,笔者借鉴听觉系统的运行机制,通过模拟耳蜗基底膜频率分解、侧抑制和时频感受野等生物学现象,提出了一种可实现谐波频率识别、提取与跟踪功能的计算方法,数值仿真和试验数据检验均获得较好效果。
1 方法的基本原理
所提方法的实现过程如图1所示。其中,带通滤波模拟耳蜗基底膜的频率分解功能,二维傅里叶变换(discrete Fourier transform, 简称DFT)用于提取各局部时频区域的频率和幅值信息,其中的幅值信息由侧抑制计算实现峰值锐化。频率点提取工作将筛选出谐波成分频率点,再将同一谐波对应的频率点归为一组,并略去与随机噪声对应的频率点,从而完成频率点重组。所得结果可描述信号的主要频率结构和各频率成分的时变情况。

图1 所提方法的实现过程
Fig.1 Schematic diagram of the proposed method
2 方法的实现
2.1 带通滤波
设被分析的信号为x(t)。使用听觉模型中常用的Gammatone基底膜滤波器组[9]进行带通滤波,设滤波器数目为M,第m个滤波器的表达式为
h(m,t)=B4t3e-2πBtcos(2πfmt+φm)
(1)
其中:fm为第m个滤波器的中心频率;相位φm通常取为零;参数B用于控制带宽。
B的计算公式为
B=1.019(24.7+0.108fm)
(2)
为避免同一频率成分在不同滤波通道中出现相位差异,在基于傅里叶变换进行卷积运算时忽略滤波器h(m,t)的相频特性,即
y(m,t)=F-1[X(f)|H(m,f)|]
(3)
其中:F-1为傅里叶逆变换;X(f)和H(m,f)分别为x(t)和h(m,t)的频域表达。
设y(m,t)的离散形式为y(m,n)(n=1,2,…,N)。
2.2 二维DFT
大脑听皮层中不同的神经元具有不同的时频感受野,即只对特定的频率和波形产生最大响应,目前,模拟这一功能的常用方法是对听觉谱进行二维DFT[10]或二维滤波[11],但听觉谱具有频率模糊性,笔者直接对y(m,n)的各时频区域做二维DFT计算。
使用二维高斯窗wij(m,n)进行时频区域选取,窗函数表达式为
(4)
其中:Wr和Wc为wij(m,n)在m和n方向上给定的宽度。
二维DFT为
(5)
其中:2L1+1和2L2+1为两个方向上的二维DFT点数。
设采样频率为fs,高斯窗覆盖的频率范围为Δf,令
Gij(p,q)实现了对y(m,n)的维数扩张,有助于提取信号中的更深层次信息。结合本研究目的,首先搜索|Gij(p,q)|中的最大值,即
A(i,j)=max{|Gij(p,q)|}
(8)
设A(i,j)对应的坐标为(Ωij,Γij),其中Ωij为wij(m,n)覆盖的时频区域内能量最大的谐波频率。
2.3 侧抑制
侧抑制[12]是视觉、听觉及触觉等感官系统中的一种生物现象,其作用是锐化边界或波峰,可提高输入信号的对比度。在本研究中,由于中心频率相近的Gammatone滤波器之间会具有较大的频率重合度,所以一频率成分往往会使A(i,j)中存在覆盖范围较大的凸起曲面,为易于实现后续的频率点提取,首先对A(i,j)进行侧抑制处理。
考虑到A(i,j)是离散的,令A(0,j)=0和A(M+1,j)=0,首先计算
AΔ(i,j)=[A(i,j)-A(i-1,j)]
[A(i,j)-A(i+1,j)]
(9)
(i∈{1,2,…,M},j∈{1,2,…,N})
对A(i,j)的侧抑制处理为
(10)
利用A1(i,j)生成频率函数ζ(i,j),即
(11)
2.4 频率点提取
频率函数ζ(i,j)是时间-滤波通道-频率空间内的离散点,但有一部分对应干扰噪声,笔者综合j时刻下ζ(i,j)中各相邻非零点的间隔与A1(i,j)的幅值信息完成谐波频率点的提取。
2.4.1 谐波频率点判据条件
信号x(t)中的某一频率分量为
x0(t)=asin(2πf0t)
(12 )
设x(t)中的白噪声为no(t),经带通滤波后,在中心频率与f0相近的滤波通道中会存在幅值明显的滤波信号,设第k个滤波器的中心频率与f0最接近,则该滤波信号为
y(k,t)=|H(k,f0)|asin(2πf0t)+nok(t) (13)其中:nok(t)为no(t)的滤波信号。
nok(t)的幅频曲线以fk为中心,其包络与|H(k,f)|相似,考虑到式(8)中只提取了|Gij(p,q)|的最大值信息,所以y(k,t)可近似表示为
y(k,t)≈|H(k,f0)|asin(2πf0t)+γksin(2πfkt)
(14)
其中:γk为nok(t)在fk处的幅值。
同理,与第k个通道相邻的滤波信号可表示为
y(k+η,t)=|H(k+η,f0)|asin(2πf0t)+
γk+ηsin(2πfk+ηt)
(15)
其中:η∈[-η1,η2],η1和η2均为正整数,理论上可取值至另一频率分量出现为止。
同时,x(t)中的其他信号分量的滤波信号可近似设为
y(m,t)≈γmsin(2πfmt)
(16)
由式(5)可知,当i∈[k-η1-Wr/2,k+η2+Wr/2]时,窗函数wij(m,n)的覆盖范围内都会包含x0(t)和干扰噪声的滤波信号,将两种滤波信号对应的幅值表达为集合的形式,即
(17)
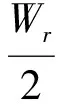
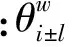
因为γi±l对应的fi±l互不相等,如果
(18)
即

其中:i′为max{Θi}对应的滤波通道数,可得Ωij=f0。
进一步考虑到高斯窗的不断平移,若一直可满足式(12)成立,则有

(i∈[k-η1-Wr/2,k+η2+Wr/2])
(19)
所以对于实测信号,若噪声水平满足
(20)
或
(21)
则可知ζ(k,j)=f0,但与其邻近的η3或η4个点处的值则均为零。
另一方面,当窗函数wij(m,n)覆盖的区域内只有干扰噪声的滤波信号时,即
A(i,j)=γi
(22)
由于噪声的随机性,γi关于i值也会具有随机性,所以经侧抑制后得到的频率函数会较为密集,很难出现较大的幅值为零的区间。
综上可得谐波频率点的判据条件:若ζ(i,j)中一非零点在i方向上与两侧相邻的非零点间的间隔都大于σ1Wr,即可认为该点对应一谐波分量,则ζ(i,j)保留原值;否则令ζ(i,j)=0。其中,σ1为给定的系数。考虑到实测信号中的干扰噪声难以避免,本研究令σ1=0.45。
2.4.2 补充条件
当信号中的两相邻谐波分量的间隔小于σ1Wr时,上述判据方法会发生漏判。当两分量的能量均大于噪声能量时,会在A1(i,j)的相应位置处存在明显幅值。因此,设j时刻下A1(i,j)的最大值为Λj=max{A1(i,j),i=1,2,…,M},若A1(i,j)≥σ2Λj,可保留ζ(i,j)原值,否则令ζ(i,j)=0。其中,σ2为给定的系数,本研究令σ2=0.1。
2.4.3 频率点提取过程示意
图2为对一混有高斯白噪声的正弦信号的频率提取过程。由图可见,A1(i,j)中只保留了A(i,j)的峰值信息,同时,在正弦信号频率附近存在宽度约为Wr的空白区间,该区间外的频率点则较为密集,对应噪声分量。由这一过程可以发现,二维高斯窗的不断平移与二维DFT可使谐波成分在时频域内具有自身的形态特征,当噪声水平一定时,其形态特征与谐波幅值关系不大,从而可保证频率点提取的准确性,还有助于提取幅值微弱的谐波频率点。

图2 频率提取过程示意Fig.2 Illustration of frequency extraction
2.5 频率点重组
频率函数ζ(i,j)是一组离散点,但其中大多数点的值为零,为便于后续工作,首先提取ζ(i,j)中的非零点。设ζ(iu,j)为ζ(i,j)中第j个时刻下的第u个非零点,u∈{1,2,…,U},U为ζ(i,j)中各时刻下非零点数目中的最大值。生成一函数ξ(u,j),令ξ(u,j)=ζ(iu,j)。
由于实测振动信号中的谐波分量数目往往较为稳定,且频率值不会在短时间内产生剧烈波动,加之前期计算中已有效降低了噪声的影响,所以同一谐波分量的频率点多会在ξ(u,j)中具有一定的连续性,即联接成段,且每段中的点对应的u坐标值相同。因此,首先从ξ(u,j)中分离出各频率点段,并计算ξ(u,j)中相邻点间的频率变化量,即
Δξ(u,j)=ξ(u,j+1)-ξ(u,j)
(23)
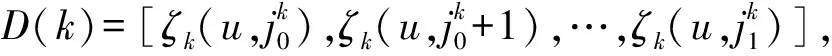
(24)
本研究取σ2=50 Hz。因同一信号分量的频率点可能会被划分成多个数据段,故以不同数据段间首尾点在时频网格中的距离最近为主要依据进行数据段组合,设两数据段D(k)和D(l)首尾点距离为

(25)
3 方法验证
3.1 仿真验证
设滤波器数目M=200,高斯窗函数参数Wr和Wc分别取为40和1 000,窗函数在时间方向的移动步长为100个点,在频率方向为1个点,其他参数在前面已给出。
生成仿真信号x(t)如下
x(t)=sin(2π1 000t3)+sin(2π3 000t2)+no(t)
其中:no(t)是方差为0.01的高斯白噪声。
计算得到的各中间结果如图3所示,包括基底膜带通滤波结果y(m,n)、二维DFT后得到的A(i,j)、侧抑制结果A1(i,j)以及频率函数ζ(i,j)。其中,图3(d)为频率值投影图。由图3可知,使用二维DFT可以有效提取各时频区域内的主要频率成分,侧抑制处理可使各频率成分在时频平面上占据的宽度变窄,从而简化了时频信息。由图3(d)可发现,有用信号与噪声信号间存在空白区域。

图3 仿真信号分析所得中间结果Fig.3 Intermediate results in simulation analysis
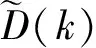

图4 函数ξ(u,j)中频率点分布情况Fig.4 Distribution of frequency points in ξ(u,j)
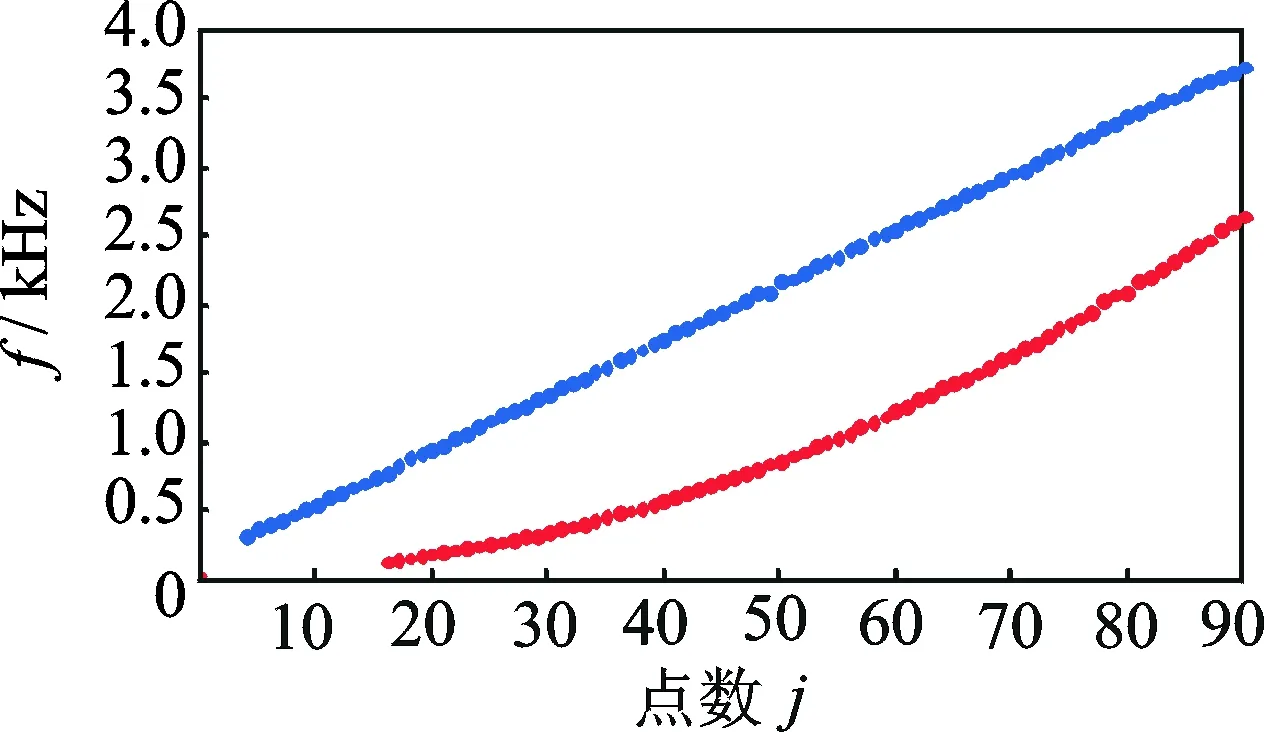
图5 频率点重组结果Fig.5 Result of frequency recombination
在图4、图5中的低频部分存在频率点丢失现象,这与窗函数的宽度Wr有关。如取Wr=10而其他参数不变,所得结果如图7所示,可见,频率点丢失现象已明显改善。同时在本研究验证中也发现,过小的Wr会导致过多的噪声频率点被漏判,因此,宜使用Wr略大的窗函数。

图6 频率重组后各数据段内点数Fig.6 Points count of data segments after frequency recombination
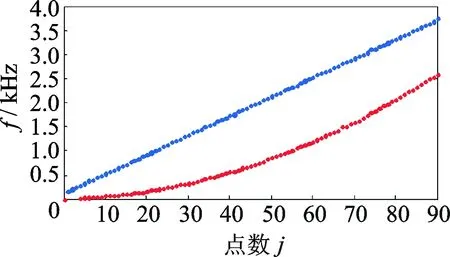
图7 Wr=10时的频率点重组结果Fig.7 Result of frequency recombination while Wr=10
3.2 试验验证
现结合两实例验证所提方法性能:a.某型涡轮泵启动过程振动信号的频率提取;b.吸尘器振动信号的谐波成分分析。
3.2.1 试验验证1
涡轮泵是一种应用广泛的旋转设备,由于结构紧凑且转子刚度与支撑刚度均较大,其振动信号中必然存在谐波成分。某型涡轮泵常出现转子振幅超标现象,使用电涡流位移传感器测试得到启动过程转子位移振动信号,如图8所示,测试时采样频率为51 200 Hz,测点位于近涡轮端。取滤波器数目M=300,Wc=3 000,窗函数在时间轴方向移动步长为150个点。带通滤波结果y(m,t)如图9所示,图中主要有涡轮泵旋转频率及其2倍频成分随时间的演变过程,但其他成分十分微弱。
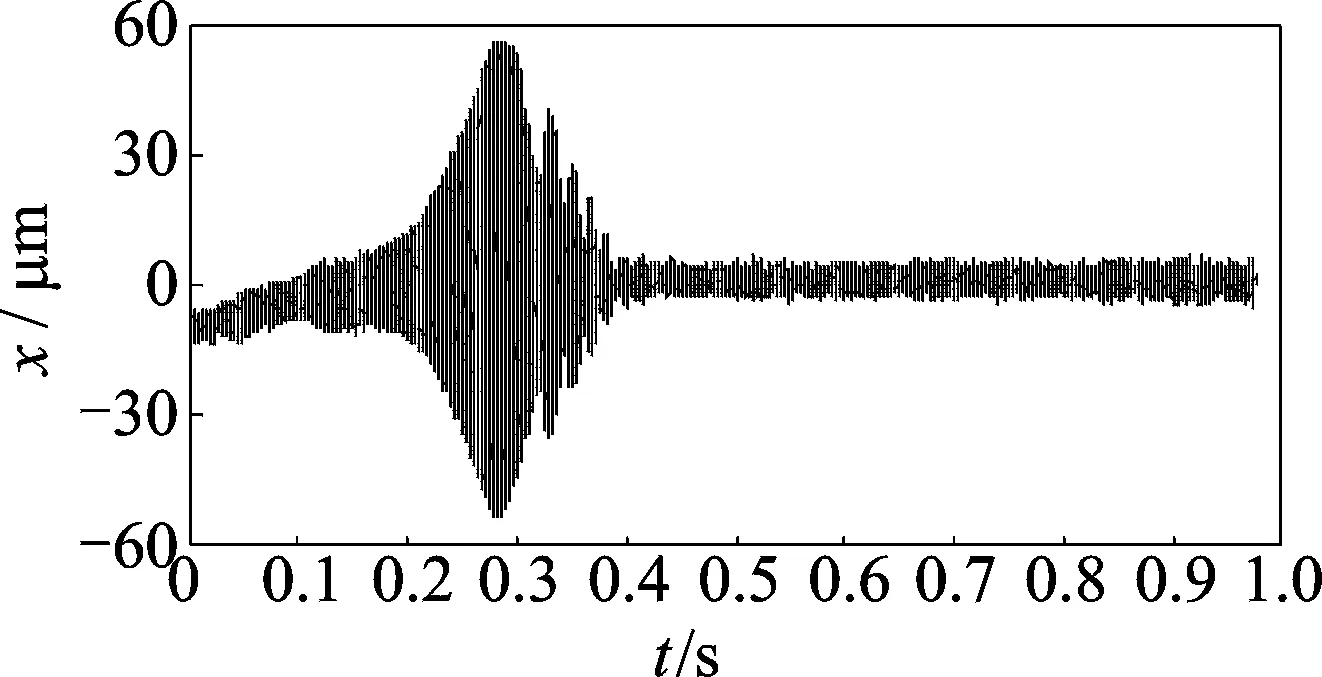
图8 涡轮泵启动过程振动信号Fig.8 Vibration signal of turbopump startk-up procedure

图9 带通滤波结果y(m,t)Fig.9 Band-pass filtering result y(m,t)
使用本研究方法做进一步分析,频率点重组后得到85个数据段,各数据段内的频率点数目如图10所示,其中12个数据段内的点数大于15,各段内的频率值如图11所示。由图11可以发现:a.所提方法可以准确地提取设备的旋转频率及其各高次倍频,且时变特征也与实际情况相符;b.信号中的微弱成分得到了有效表征。除了旋转频率的高次倍频成分外,当设备稳速运行时,在低于旋转频率的频段内存在一断续出现的频率成分,虽然这一成分在图9中亦隐约可见,但无法明确其具体性质,而根据图11则可判断为谐波成分。在其出现的时段内,旋转频率为1 331Hz,低频成分的频率值为512Hz左右,为旋转频率的0.38倍,考虑与轴承保持架振动有关。
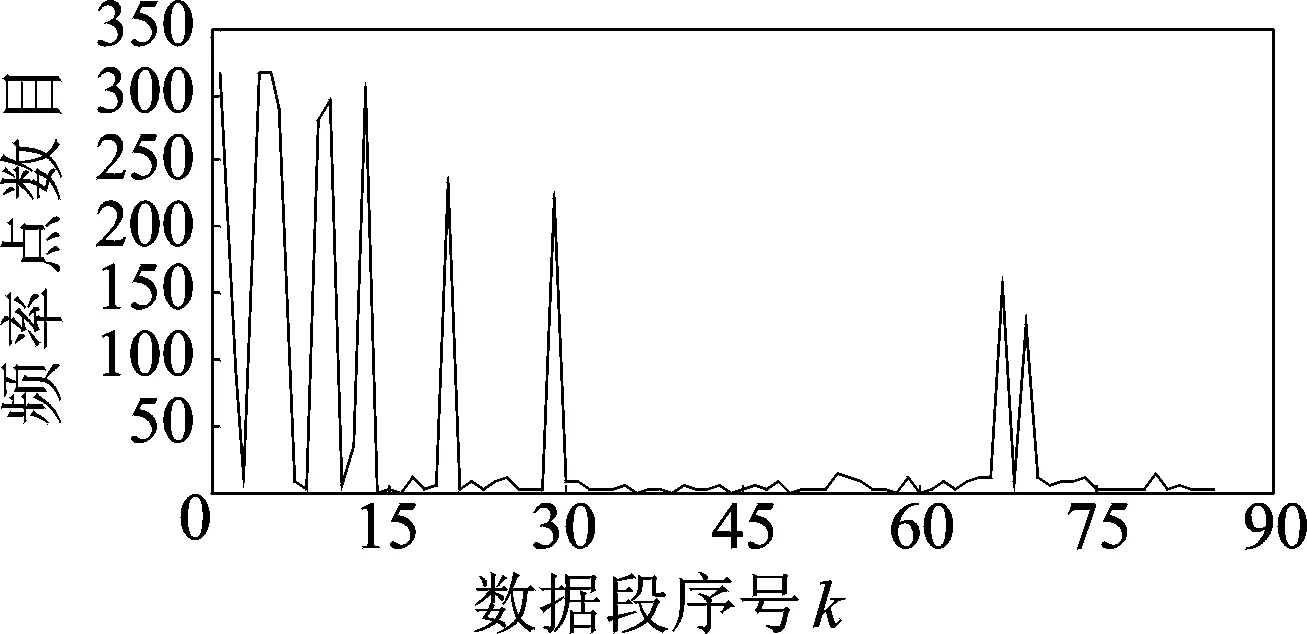
图10 频率重组后各数据段内点数Fig.10 Points count of data segments after frequency recombination

图11 频率点重组结果Fig.11 Result of frequency recombination
综合上述计算结果,推测涡轮泵转子轴系和轴承两部分的装配质量欠佳,改进相关装配工艺后,振动超标问题得以改善。
3.2.2 试验验证2
图12为某型卧式吸尘器,在对该产品的噪声控制方法研究过程中进行了机体的振动测试。该设备的核心部件为串励电机和风机,电机工作转速约为3.9×104r/min,额定功率为1.5kW,风机叶片数为9。吸尘器的主要激励源是电机和与之相联的风机,而电机的转速单一且稳定,所以,振动信号中必然存在电机的旋转频率成分和风机的通过频率成分。

图12 吸尘器与振动测点布置Fig.12 Cleaner and vibration measurement points arrangement
在吸尘器工作状态下进行振动测试,采样频率为19 692Hz,测得的部分信号波形如图13所示。

图13 吸尘器振动信号Fig.13 Vibration signal of cleaner
使用本研究方法分析所测信号,相关参数与试验1相同。带通滤波结果如图14所示,图中的低频部分可见一稳定的谐波分量,但难以明确其他谐波成分。图15为频率重组后各数据段内的频率点数目情况。频率重组结果如图16所示,图中在98,662,1 325和5 947 Hz频率处存在十分稳定的信号分量。结合电机与风机参数并考虑到二维DFT的频率误差可知:98 Hz对应电机的电磁振动;662和1 325 Hz分别为电机的旋转频率及其二倍频;5 947 Hz则对因风机叶片的通过频率;而在图14中只能明确98 Hz这一频率成分。
做为对比,图17为信号的幅值谱及其局部放大,图中,除了98Hz处可见明显的离散谱线,其他3个频率处的谱线均不突出或被淹没在由气流导致的随机振动频率成分中,如1 325Hz处的谱线无法确定对应的是周期成分还是随机振动成分,而5 947 Hz处的谱线幅值又极其微弱,约为98Hz频率处幅值的0.005倍。由于本研究方法在提取频率点过程中以频率点间的间隔为主要判断依据,所以能够较好地提取微弱的频率成分,并具有一定的抗噪声干扰性能。
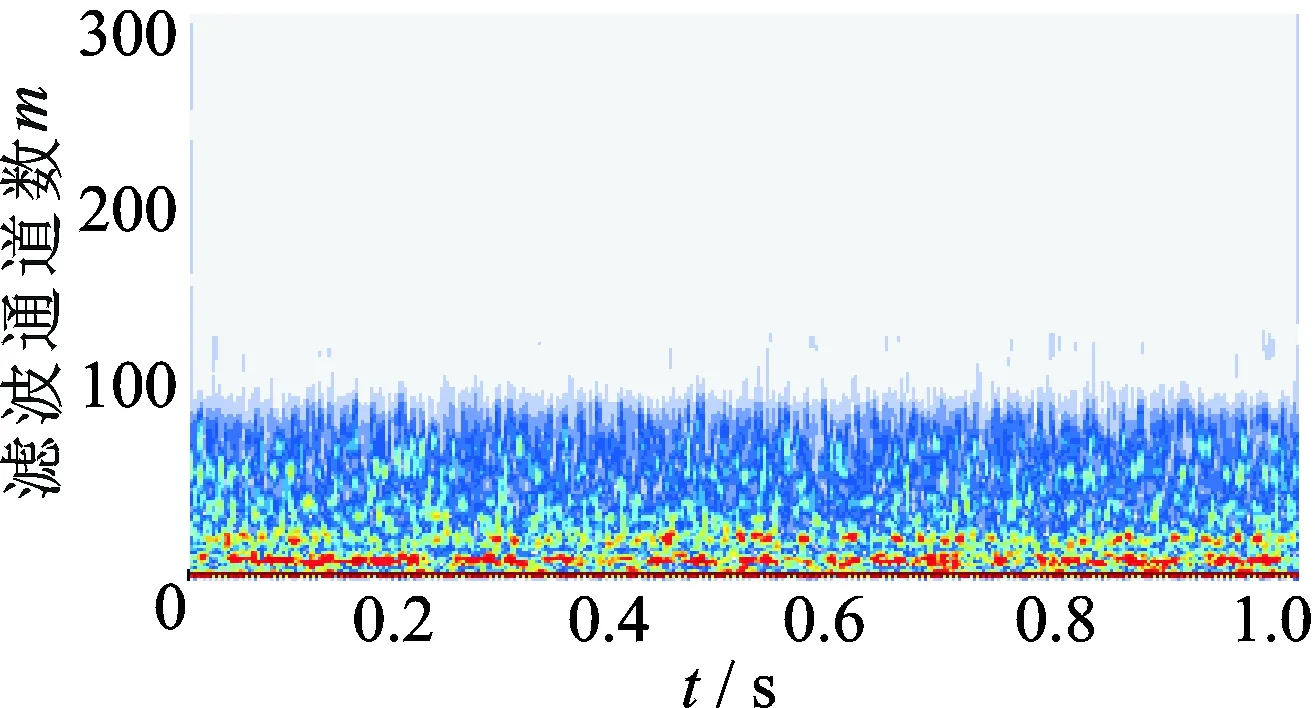
图14 带通滤波结果y(m,t)Fig.14 Band-pass filtering result y(m,t)

图15 频率重组后各数据段内点数Fig.15 Points count of data segments after frequency recombination
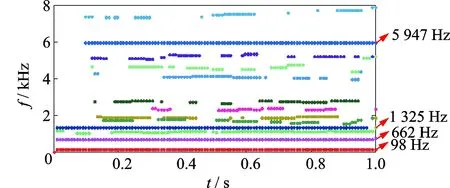
图16 频率点重组结果Fig.16 Result of frequency recombination

图17 吸尘器振动信号幅值谱Fig.17 Frequency spectrum of vibration signal of cleaner
4 结 论
1) 基于听觉系统的时频感受野功能特性,对信号的不同时频区域进行二维DFT计算,可提取各区域内的主要谐波频率,并可精简信号的时频信息。
2) 经侧抑制计算后,谐波与随机成分对应的频率点呈现不同的分布状态,可根据频率点间的频率间隔进行谐波成分频率点的识别和提取,从而具有一定的抗噪声干扰能力,并有可能提取到幅值微弱的谐波成分频率点。
3) 由于所提方法可自动实现对信号频率结构的描述,对于时变信号又具有频率跟踪功能,从而可为设备状态监测提供辅助信息。
4) 由计算过程可知,对于具有密集频谱特点的信号,该方法尚无法保证准确提取所有谐波成分频率点,这也将在后续工作中进行研究。
[1] 杨凯,丁开平,杨云鹤. 基于信号时频分析理论识别时变模态参数实验[J].振动、测试与诊断,2015,35(5):880-884.
Yang Kai, Ding Kaiping, Yang Yunhe. Experimental investigation on estimation of time-varying modal parameters using time-frequency analysis[J].Journal of Vibration,Measurement & Diagnosis, 2015,35(5):880-884.(in Chinese)
[2] 肖良瑜,李建伟,宋大凤,等.立式屏蔽电机半速涡动异常振动试验分析[J].振动、测试与诊断, 2015,35(2):316-321.
Xiao Liangyu,Li Jianwei,Song Dafeng,et al. Analysis of abnormal vibration of half speed eddy for vertical canned motor[J].Journal of Vibration, Measurement & Diagnosis, 2015,35(2):316-321. (in Chinese)
[3] 甄莉,彭真明. 基于广义S变换的图像局部时频分析[J].航空学报,2008,29(4):1013-1019.
Zhen Li, Peng Zhenming. Local time-frequency analysis of images based on generalized S-transform[J]. Acta Aeronautica et Astronautica Sinica,2008, 29(4):1013-1019. (in Chinese)
[4] 黄朝明,于洪亮,关德林,等. 摩擦振动时频图像特征提取[J].振动与冲击,2012,31(7):46-49,62.
Huang Chaoming, Yu Hongliang, Guang Delin, et al. Feature extraction of frictional vibration based on time-frequency image[J]. Journal of Vibration and Shock, 2012,31(7):46-49,62. (in Chinese)
[5] 权贝贝. WinCE平台下信号采集与处理系统的开发[D].沈阳:东北大学,2014.
[6] Du Yi, Kong Lingzhi, Wang Qian, et al.Auditory frequency-following response: a neurophysiological mea-sure for studying the “cocktail-party problem”[J]. Neuroscience and Biobehavioral Reviews, 2011, 35 (10):2046-2057.
[7] 李洋,唐佳,付子英,等. 听觉中枢神经元对声信号的识别和处理[J]. 生物化学与生物物理进展,2011,38(6):499-505.
Li Yang, Tang Jia, Fu Ziying, et al. Sound signal recognition and processing of central auditory neurons[J]. Progress in Biochemistry and Biophysics,2011,38(6):499-505.(in Chinese)
[8] 刘冬云,赵岩,肖中举. 短声改变听觉中枢下丘神经元对纯音的反应特性[J].华南国防医学杂志,2013,27(8):536-539.
Liu Dongyun, Zhao Yan, Xiao Zhongju. Click change the response property of inferior colliculers neurons to tone of mouse[J]. Military Medical Journal of South China,2013,27(8):536-539. (in Chinese)
[9] 李允公,张金萍,戴丽. 基于极值点概率密度和听觉模型的瞬态信号提取方法研究[J].振动与冲击,2015,34(21):37-44,53.
Li Yungong, Zhang Jinping, Dai Li. A method for extracting transient signal based on the probability density of extreme points and auditory model[J]. Journal of Vibration and Shock, 2015,34(21):37-44,53. (in Chinese)
[10] Ezzat T, Bouvrie J, Poggio T. Max-Gabor analysis and synthesis of spectrograms[C]∥Ninthinternational Conference on Spoken Language Processing(ICASLP 2006). New Your: Gurrant Associates, 2006:17-21.
[11] Coensel B D, Botteldooren D. A model of saliency-based auditory attention to environmental sounds[C]∥Proceedings of 20th International Congress on Acoustics, (ICA 2010).New York: Gurrant Associates,2010:23-27.
[12] 徐新洲,罗昕炜,方世良,等. 基于听觉感知机理的水下目标识别研究进展[J].声学技术,2013, 32(2): 150-158.
Xu Xinzhou, Luo Xinwei,Fang Shiliang,et al. Research progress of underwater target recognition based on auditory perception mechanism[J]. Technical Acoustics, 2013, 32(2):150-158.(in Chinese)
10.16450/j.cnki.issn.1004-6801.2017.06.008
国家自然科学基金资助项目(51275080)
2016-03-02;
2016-06-04
TH17

李允公,男,1976年6月生,博士、副教授。主要研究方向为机械故障诊断、工程信号分析等。曾发表《Auditory-model-based feature extraction method for mechanical faults diagnosis》(《Chinese Journal of Mechanical Engineering》2010,Vol.21,No.3 )等论文。
E-mail: ygli@mail.neu.edu.cn

