振动传递路径系统的参数和全局灵敏度分析

张义民, 仝 允

(1.沈阳化工大学装备可靠性研究所 沈阳, 110142)(2.中国电子科技集团公司第38研究所 合肥, 230031)

◀专家论坛▶

振动传递路径系统的参数和全局灵敏度分析

张义民1, 仝 允2

(1.沈阳化工大学装备可靠性研究所 沈阳, 110142)(2.中国电子科技集团公司第38研究所 合肥, 230031)

提出了振动传递路径系统响应对系统参数和传递路径的全局灵敏度分析的数值方法。考虑结构参数的随机性，获取各传递路径受体输出响应的随机统计特征，以及路径中系统参数对受体振动响应的定量影响关系。基于文中数值方法，可以定量表述影响振动传递路径系统中受体振动特性大小的路径重要度排序以及系统参数的灵敏度排序。以典型多自由度振动路径分析模型为例，讨论了随机振动系统传递路径重要度分析过程，通过与Monte-Carlo随机模拟结果相对比，验证了本方法的正确性与可行性。

随机摄动法; 振动传递路径; 全局灵敏度分析; 重要度排序

引 言

在机械结构系统中，振动和噪声将会影响整个结构系统的性能，甚至造成零部件失效和结构系统的失效，因此降低结构系统的振动和噪声是现代机械设计的重要研究课题之一。振动系统通常包含3个部分：振动源、振动传递路径和振动接受体。传递路径是指振动由振动源经特定的媒介物传递至接受结构所经过的物理介质。如汽车动力总成系统，工作时产生的激振力通过悬置系统传递到车身和座椅，诱发车身结构发生振动，降低乘坐舒适性，因此有必要开展由于路面和发动机等激励源的能量在系统各个传递路径中的传递规律的研究。明晰随机结构系统的振动与噪声的传递规律，清楚结构系统物理参数对接受体振动量的影响程度，对于有效地采取隔振、吸振、消振等减振降噪的措施以及降低结构系统的振动与噪声有着非常重要的价值。目前，振动系统传递路径的分析主要采用的是实验方法和能量传递方法[1-5]。

基于随机摄动法[6-8]和振动系统传递路径灵敏度分析[9-10]，笔者提出了一种时域内计算系统参数灵敏度和传递路径灵敏度的有效方法，定义了相应的系统参数灵敏度指标和传递路径灵敏度指标。本方法能够方便地对具有多个传递路径的振动系统进行传递路径灵敏度排序，同时给出影响系统响应的重要系统参数。

1 振动传递路径系统模型

1.1 振动系统模型

为了研究振动系统参数对各个传递路径响应的影响，首先要明确激励(输入)和响应(输出)之间的联系。图1为5个自由度的振动系统模型，其中仅有一个激励输入。图中字母下标s表示振动源，p表示传递路径，r表示接受体。对应的路径1、路径2和路径3上的质量m、刚度k及阻尼c见图1。

图1 振动传递路径系统Fig.1 The model of vibration transfer path systems

根据牛顿定律，图1所示的振动系统的微分方程式可以表示为

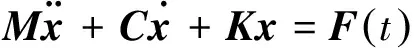
(1)

其中

M=diag[msmp1mp2mp3mr]

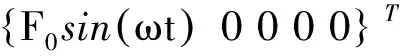
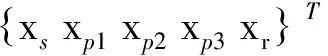
在式(1)中，质量、阻尼和刚度系数为该振动系统的随机参数，组成随机参数向量b15×1= [mp1,mp2,mp3,csp1,csp2,csp3,crp1,crp2,crp3,ksp1,ksp2,ksp3,krp1,krp2,krp3]T。可见,该振动系统的运动微分方程可以整理为

(2)

1.2 随机摄动法

(3)

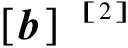
(4)

(5)

(6)

将式(6)代入式(5)，得到振动传递路径系统响应的方差矩阵。为了提高计算效率，在计算方差灵敏度的过程中只涉及到一阶灵敏度。如果要提高计算精度，也可以计算二阶及更高阶的灵敏度，但是会增加一些繁杂的计算。

2 系统参数及传递路径灵敏度

振动传递路径系统的振动和噪声的控制主要包括两个方面：系统组成部分及零部件的振动控制和传递路径的振动控制。为了研究振动传递路径系统响应对系统参数的灵敏度，以式(4)和式(5)系统位移响应方差的通用分解理论为基础，定义振动传递路径系统随机位移响应x对系统参数bi的灵敏度指标为

1,2,…,s)

(7)

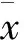
式(7)可以用来表示参数bi对位移响x概率统计分散性的参数灵敏度，由此根据方差分析有

(8)

(9)

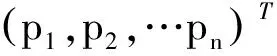
；k∈i)

(10)

其中：P′为振动路径pj中随机参数bi的方差贡献量；P″振动路径pj的总方差；bk为第j条传递路径的随机参数，该灵敏度指标表示为路径j上的振动系统响应对其所在路径上的系统参数的灵敏度。

由以上定义可知，若以振动传递路径系统受体的响应xr为例，各个随机参数、传递路径以及路径参数的灵敏度指标分别为

(11)

(12)

(13)

通过以上公式计算，可以得到振动传递路径系统接受体的响应对系统参数的灵敏度和对各个传递路径的灵敏度，即可以找到影响振动传递路径系统接受体响应的某个或某几个重要参数和重要的传递路径，这样就可以有的放矢地解决振动或噪声控制等问题。

3 算 例

如图1所示的5个自由度振动系统模型，振动传递路径系统的质量、阻尼和刚度的值分别为：ms= 0.5 kg，cs= 1 N·s/m-1，ks= 500 N/m；mr= 0.5 kg，cr= 1 N·s/m，kr= 180 N/m。激励值为：F0= 10 N，激励频率ω= 10 rad/s。传递路径上的各个随机参数向量为：b15×1= [mp1,mp2,mp3,csp1,csp2,csp3,crp1,crp2,crp3,ksp1,ksp2,ksp3,krp1,krp2,krp3]T。其中各个随机参数均服从正态分布，其均值分别为：mp1= 0.4 kg，mp2= 0.5 kg，mp3= 0.6 kg，csp1=crp1= 6 N·s/m，csp2=crp2= 4 N·s/m，csp3=crp3= 8 N·s/m，ksp1=krp1= 800 N·s/m，ksp2=krp2= 600 N·s/m，ksp3=krp3= 400 N·s/m，且变异系数均为0.05,试确定该振动传递路径系统的传递路径灵敏度和系统参数灵敏度。

图2 时域范围内的响应均值变化曲线Fig.2 The curve of mean value of responses with regard to time t

图3 时域范围内输入响应xs和输出响应xr的方差及其协方差变化曲线Fig.3 The variance of xr,xsand the covariance of xr and xs with regard to time t

将所给定的振动传递路径系统的参数和激励的参数代入运动微分方程，并应用Newmark-β方法进行求解，得到计算结果如图2和图3所示。图2和图3分别给出了在时域范围内的输入响应xs和输出响应xr的均值变化曲线以及输入响应xs和输出响应xr的方差与协方差变化曲线,其中：广义概率摄动方法(generalized probabilistic perturbation method,简称GPPM);Monte-Carlo模拟(Monte-Carlo simulation,简称MCS)。

为了验证研究方法计算结果的准确性，同时给出了Monte-Carlo方法计算结果的对比。从图2和图3中的计算结果可以看出，基于随机摄动法计算的振动传递路径系统响应结果和基于Monte-Carlo仿真结果基本吻合。

图4给出了输出响应xr对各系统参数的灵敏度变化曲线，图5给出了输出响应xr对各传递路径的灵敏度变化曲线。其中,实线为随机摄动法-GPPM的计算结果曲线，虚线为Monte-Carlo仿真-MCS的计算结果曲线。

从图4的计算结果可以看出，振动传递路径系统的输出响应xr对系统所有参数的灵敏度大小依次为mp3,mp2,mp1,ksp3,ksp2,ksp1,krp3,krp1,csp3,csp2,krp2,csp1,crp3,crp1,crp2。其中：xr对质量参数的灵敏度大小依次为mp3,mp2,mp1；xr对刚度参数的灵敏度大小依次为ksp3,ksp2,ksp1,krp3,krp2,krp1；xr对阻尼参数的灵敏度大小依次为csp3,csp2,csp1,crp3,crp1,crp2。从图5的计算结果可以看出，振动传递路径系统的输出响应xr对各传递路径的灵敏度大小依次为路径3、路径2、路径1。

根据定义式(13)的某条路径上振动传递路径系统输出响应xr对系统参数的灵敏度，计算得出的第3条传递路径上的振动传递路径系统响应xr对系统参数的灵敏度变化曲线如图6所示。

从图6的计算结果可以看出，在第3条传递路径上，系统参数对输出响应影响的大小依次为mp3,ksp3,krp3,csp3,ccp3。

图4 输出响应xr对各系统参数的灵敏度变化曲线Fig.4 The sensitivity of each parameter to the receiver xr with regard to time t

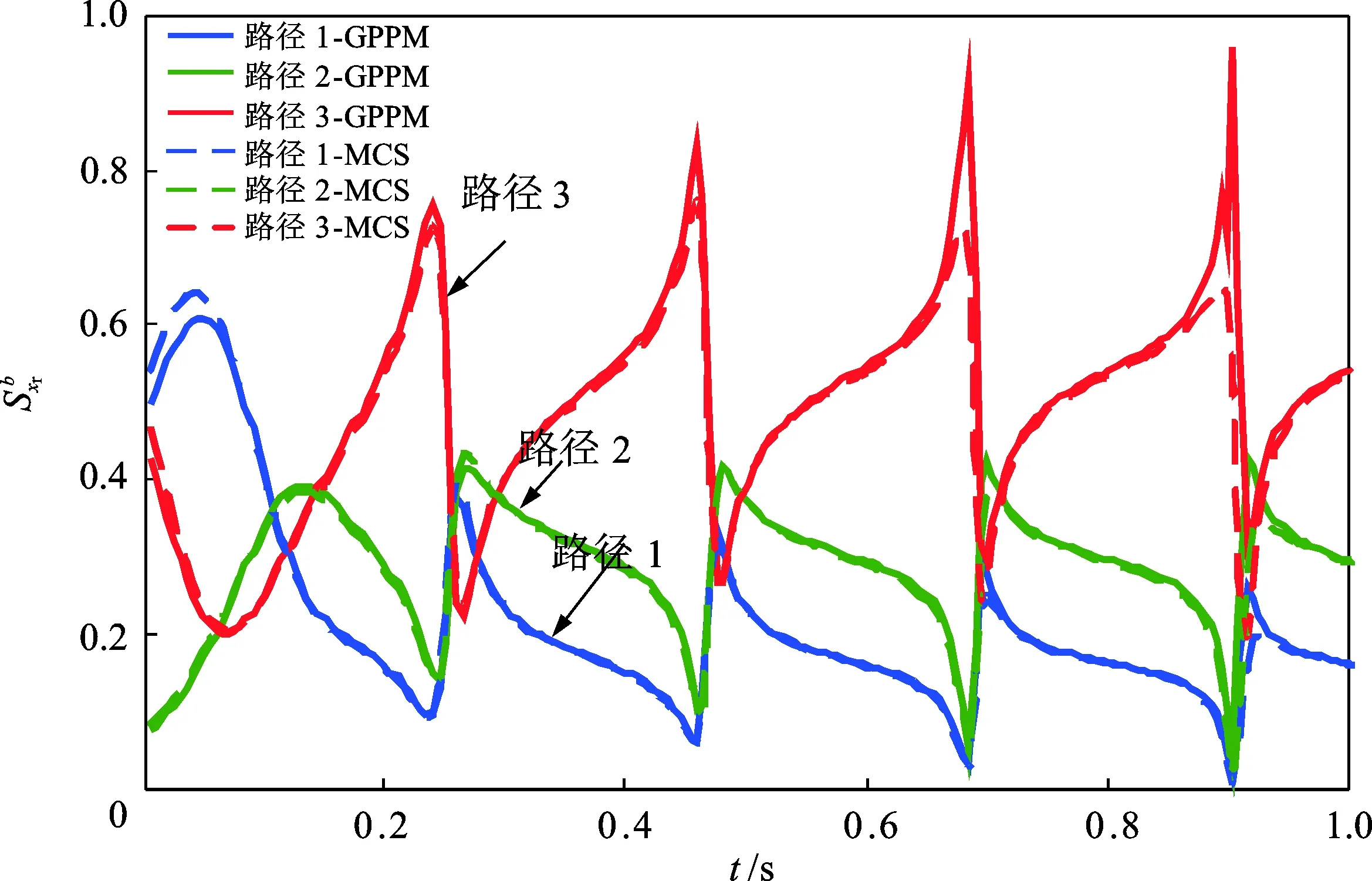
图5 输出响应xr对各传递路径的灵敏度变化曲线Fig.5 The sensitivity of each path to the receiver xr with regard to time t

图6 第3条传递路径上各个系统参数对输出响应xr的灵敏度变化曲线Fig.6 The sensitivity of each parameter in path 3 to the receiver xr with regard to time t

4 结束语

由振动传递路径系统响应对系统参数和传递路径的灵敏度可以方便有效地给出系统参数和传递路径对振动传递路径系统响应的影响排序。笔者提出了振动传递路径系统对系统参数和传递路径的灵敏度分析方法，定义了系统参数灵敏度指标和传递路径灵敏度指标，可以明确指出对传递路径系统影响重要的参数和重要的路径，为有针对性的进行振动控制和噪声限制设计提供了创新概念和思路。另外，用传递路径系统的振动和噪声的识别和控制方法，进行了时域范围内的振动传递路径系统响应对系统参数和传递路径的灵敏度的计算与分析，并且与Monte-Carlo方法进行了比较，符合的很好，为实际工程的应用打下了坚实的基础。

[1] Lyon R H, Dejong R G. Theory and application of statistical energy analysis[M].Boston: Butterworth-Heinemann, 1995.

[2] Wohlever J L, Bernhard R J.Mechanical energy flow models of rods and beams [J]. Journal of Sound and Vibration, 1992, 153(1): 1-19.

[3] Singh R, Kim S.Examination of multi-dimensional vibration isolation measures and their correlation to sound radiation over a broad frequency range [J]. Journal of Sound and Vibration, 2003, 262(3): 419-455.

[4] Cremer L, Heckl M. Structure-borne sound: structural vibrations and sound radiation at audio frequencies [M]. [S.l.]:Springer Science & Business Media, 2013.

[5] Kim S, Singh R. Vibration transmission through an isolator modelled by continuous system theory [J]. Journal of Sound and Vibration, 2001, 248(5): 925-953.

[6] Zhang Yimin, Chen Suhuan, Liu Qiaoling, et al. Stochastic perturbation finite elements [J]. Computers & Structures, 1996, 59(3): 425-429.

[7] Zhang Yimin, Wen Bangchun, Chen Suhuan. PFEM formalism in Kronecker notation [J]. Mathematics and Mechanics of Solids, 1996, 1(4): 445-461.

[8] Wen Bangchun, Zhang Yimin, Liu Qiaoling. Response of uncertain nonlinear vibration systems with 2D matrix functions [J]. Nonlinear Dynamics, 1998, 15(2): 179-190.

[9] Zhang Yimin, Huang Xianzhen, Zhao Qun. Sensitivity analysis for vibration transfer path systems with non-viscous damping [J]. Journal of Vibration and Control, 2011, 17(7): 1042-1048.

[10] Zhang Yimin, Huang Xianzhen. Sensitivity with respect to the path parameters and nonlinear stiffness of vibration transfer path systems [J]. Mathematical Problems in Engineering, 2010, 2010:650247.

[11] Vetter W J.Matrix calculus operations and Taylor expansions[J]. SIAM Review, 1973, 15(2): 352-369.

10.16450/j.cnki.issn.1004-6801.2017.06.001

国家自然科学基金资助项目(51675216)；国家重点基础研究发展计划(“九七三”计划)资助项目(2014CB046303)

2017-01-10；

2017-01-20

TB123; TH113

张义民，男，1958年9月生, 博士、教授、博士生导师、长江学者。主要研究方向为机械可靠性工程、机械动态设计等。曾发表《机械可靠性设计的内涵与递进》(《机械工程学报》2010年第46卷第14期)等论文。

E-mail:ymzhang@mail.neu.edu.cn