基于高频采样法的轴系扭振测试新方法

郭文新， 李志深， 李富才， 静 波， 李鸿光

(上海交通大学机械系统与振动国家重点实验室 上海，200240)

基于高频采样法的轴系扭振测试新方法

郭文新， 李志深， 李富才， 静 波， 李鸿光

(上海交通大学机械系统与振动国家重点实验室 上海，200240)

针对现有扭振测试和分析通常采用硬件实现，工业现场应用不便的问题，提出一种基于高频采样的轴系扭振测试新方法。该方法利用由电涡流传感器或磁电传感器采集到的测速齿盘转速信号，对时域信号进行3次样条插值，结合3点卷积幅值校正方法对信号进行频谱分析，从而实现轴系扭振测试与分析。通过数值仿真和实验对其进行验证，并与扭振分析仪器结果对比，表明本方法提取的扭振信号特征准确。

高频采样； 扭振； 测试； 3次样条； 3点卷积

引 言

轴系是所有回转机械设备中最重要的结构部件，主要承担传递扭矩的任务，其安全可靠的工作是所有回转设备发挥功效的最基本前提。但自旋转机械出现以来，断轴事故时有发生。经过对美国加利福尼亚爱迪生公司的Mohave电厂1号机组曾连续两次发生断轴事故[1]的研究，人们认识到扭转振动是其发生的罪魁祸首。自此以后，国内外发生的30多起机组轴系损坏事故都与扭振相关[2]。扭振作为轴系最基本的振动形式之一，如不加以控制，轻则引起较大噪声，加剧其他零件的磨损，重则发生轴系断裂的恶性事故。总之，扭振是普遍存在并应引起足够重视的问题[3-5]。扭转振动具有普遍性、潜伏性、引发事故的突发性和严重性的特点，因此轴系扭振的测量工作尤为重要。各国船规中明文规定扭振特性的审查内容包括理论计算和实测结果，若两者不同，则以实测结果为准[1]。由此可见，高效精准的扭振测试方法、便捷经济的测量系统有很大的存在价值。

轴系扭振测量主要分为接触式测试和非接触式测试[6]。目前的扭振仪多属非接触式测试仪器，但大部分仍是模拟电路式，需要专用的模拟电路处理单元提取扭振信号进行进一步分析，每次使用前需要校正，而且模拟电路本身也会因使用时间的增加和环境的变化，产生由模拟电子器件引起的不可避免的误差。针对以上问题，董大伟等[7]提出一种基于PC的扭振测量系统(torsional vibration measurement system, 简称TVM)，充分利用PC的资源，实现了硬件上的集成性。其采用的是一种称作高频计数法的方式进行信号测量，仍需特定的硬件支持，集成度不高，不利于弯、扭等多种信号的测试工作的展开，增加了测试成本，而且由高频计数法所带来的固有限制也有待改善。基于此，随着如今PC性能的提高，为充分利用PC资源，节约成本，笔者提出一种基于高频采样法的轴系扭振测试新方法，利用通用的数采模块，结合先进的数字信号处理技术，可实现扭振信号和其他振动信号的联合测试。

1 扭振信号的提取

任何轴系都不是绝对的刚体，存在一定的柔性。在工作过程中，由于载荷或动力源的扭矩波动，轴系不同位置因为柔性而产生交变的剪应力，对轴系造成破坏，表现为在工作转速上叠加一个速度波动。基于扭转振动的这一外在表现特征，近些年来对此进行了各种提取方法的研究。其中，非接触式测量方法一般是用等分齿盘和磁电式/光电式传感器进行信号测试。

1.1 信号特征

轴系在正常工作时由于外界条件的变化而引起的扭转振动通常较微弱。当扭振发生时，由传感器测到的信号实际是工作转速下的调制信号，表现为对速度信息的幅值调制和对转过每个齿时间信息的相位调制。由于信号的微弱性，所以这种调制也是很微弱的，因此对频率解调和幅值解调的精度要求很高。

1.2 测量原理及高频计数法

由于非接触法测量的优越性，最近几十年的测量系统都是基于非接触法发展起来的。它是利用轴上的等分齿形结构或额外加在其上的等分齿轮随其同步运动时在非接触传感器中产生的脉冲，这些脉冲的间隔可以反映出轴的瞬时速度大小，通过对其解码获取扭转信息，而获得该脉冲间隔的方法通常采用高频计数法。

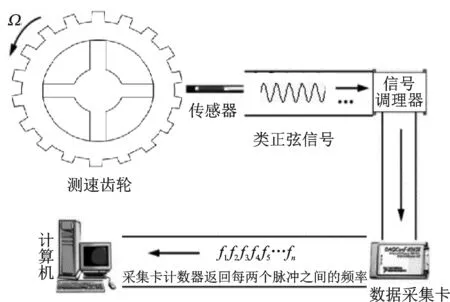
图1 扭振测量系统简图Fig.1 The torsional vibration measurement system schematic

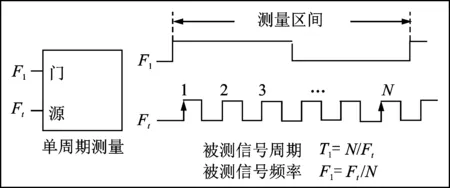
图2 计数器工作原理图Fig.2 Counter working principle diagram

如图1所示，基于高频计数法的扭振测量系统主要由测速齿盘、磁电式速度传感器、信号调理器、数据采集卡和计算机等组成。随轴同步运动的等分齿轮在磁电传感器中感应出类正弦波形，此波形即是携带扭转信息的调制信号。该信号属微弱信号，不足以推动后面为高频计数法所设计的门电路工作，因此需要调理器对其进行限幅、整形及放大等处理，最后输出恒幅矩形脉冲信号。图2为计数器工作原理图[8]。由信号调理器输出的矩形脉冲信号F1的上升沿推动门电路工作，由高频、高精度的晶振产生的高频时钟脉冲信号Ft对其进行计数，即可得到每个信号齿轮轮齿转动对应的晶振次数。代表时间信息的一连串数字随后被送入PC进行进一步处理。为达到所需精度，Ft一般取20MHz～50MHz。

1.3 相关的问题

高频计数法与之前的测试方法相比，有其独特的优势，比如提高了测量精度，简化了模拟测量扭振仪的电路结构，利用了PC的强大处理能力，提高了对扭振信号的后期分析的自动化。随着转子系统转速范围的扩大，个人计算机快速发展，价格大幅下降，高频计数法的劣势逐渐显现，具体表现如下。

1) 计数溢出问题

高频计数法的测量精度与测量转速和计数器晶振频率有关，设测量转速为n(r/min)，计数器晶振频率为fm(Hz)，测速齿盘的齿数为Z，则转过一个轮齿计数器的脉冲数为

nf=60fm/Zn

(1)

由此引入的相对量化误差为

ε=1/nf=Zn/60fm

(2)

由式(2)可知，量化误差随齿盘齿数的增加而增加，因此齿盘齿数不是越大越好。计数器能储存的最大数为2w-1，其中w代表计数器位数。测试系统做好后所有参数就已选定，当转速过低时，nf很有可能超过计数器最大值而溢出。因此，基于高频计数法的扭振测试系统对最低可测转速有要求。

2) 测量范围问题

扭角分辨率的计算公式[9]为

δ=360n/60fm=6n/fm

(3)

由式(3)可知，测量精度和测量转速成反比，和计数器晶振频率成正比。当fm选定后，为保证一定的测量精度，测量转速的最大值有限制。

3) 硬件老化等带来的精度问题

由测量原理及高频计数法部分介绍可知，基于高频计数法的扭振测量系统的硬件核心是围绕计数器和高频晶振展开的，信号调理器是不可或缺的一部分，计数器的准确计数和晶振的稳定起振都是准确测量的关键。但随着使用时间的增长，调理器的元器件老化及晶振和计数器的漂移现象的发生，数字电路中最常用的反相器的时间延迟现象的发生，都使得系统测量精度受到影响。此外，由于外界环境中存在的随机冲击噪声，环境电磁噪声常常会引起某测量周期中的多齿现象，这也给后续的信号处理带来了困难。

4) 通用性问题

围绕高频计数而引入的硬件部分在通用的数据采集设备内一般不被考虑，如有考虑也将大大增加设备成本，由此带来的问题是扭振测试工作需要专用性的硬件，这给横振、纵振及扭振的联合测试带来了障碍。因此，测试设备通用性有待提高。

1.4 本系统的实现

时域信号包含了旋转机械的运行状态特征，因而笔者所提取的特征均从时域信号中提取。基于以上几点问题的考虑，经过改进的一种高精度的基于高频采样法的扭振测试系统如图3所示。

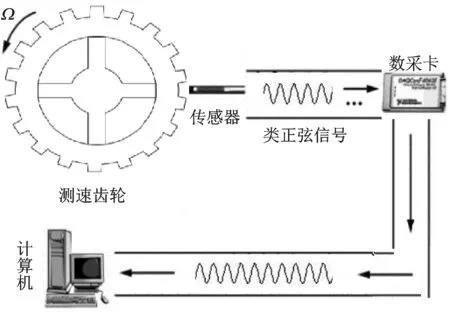
图3 新型扭振测试系统简图Fig.3 A new torsional vibration test system

该型扭振测试系统主要由测速齿盘或其他等分机构、磁电式速度传感器或光电位移传感器、通用数据采集卡及个人计算机组成。由于采用的是高频采样法，因此简化了系统的硬件要求，可以完全避免由高频计数法而带来的相关问题。该系统减弱了对硬件的要求，把以前主要由硬件完成的工作交由计算机端的软件来完成，提高了对计算机的利用率，相关参数可由程序根据公式自动选取(也可人为设定)，保证精度而又避免了测量范围受限的问题。其核心是计算机端的数字信号处理部分。

由传感器感应出的带有扭振信息的类正弦信号经过一般数据采集卡进行采样，然后把数字信号送入计算机进行进一步提取。设fs为采样频率，fmax为信号的最高频率成分，由采样定理可知，当fs>2fmax时，信号所携带的信息将会被保留。携带有扭振信息的信号是调频信号，相位信息精确提取是关键，但一般数据采集卡的采样频率不能满足精确提取相位信息的要求，此处采用零点插值法间接提高采样频率。扭振信号提取过程如下。

1) 设xi和xi+1分别为相邻的两个数据点，i和i+1分别代表数据位置，根据式(4)～式(6)寻找满足条件的xi和xi+1

xixi+1<0

(4)

xi>0

(5)

xi+1<0

(6)

2) 利用第i个数据之前的n个数据和第i+1个之后的n个数据共2(n+1)个数据进行3次样条拟合，在第i个和第i+1个数据之间进行k点3次样条插值。

3) 对插值生成的k点数据进行如步骤1所示的过程再进行零点前后数据的搜索，得到xm和xm+1。

4) 应用线性插值方法得到零点位置

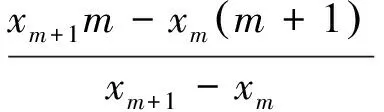
(7)

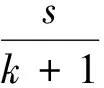
Tj=[P(j+1)-P(j)]/fs

(8)

5) 设Z为测速齿盘齿数，M为周期平均的循环数，m为齿平均数。瞬时转速ni的计算见式(9)，式(10)和式(11)是对瞬时转速进行周期平均和齿平均，目的是降低测试过程中引入到扭振信息中的噪声

(9)

(10)

(11)

6) 计算平均转速nci

(12)

7) 假设转过各齿的瞬时转速不变，计算转过第i个齿时轴系的扭角θi1

θi1=6(ni-nci)Ti

(13)

8) 计算轴系扭角θi

(14)

至此，即获得轴系扭转振动的时域波形。图4为该算法的具体流程图。由图4可以看出，除前面介绍的步骤外，引入一个判断分支，主要目的是剔除由于随机噪声引入的虚假零点，0.5的裕度值既可以达到该目的，也为设备的升降速过程提供了空间。在计算完该次平均转速时，根据约束测量精度的公式对M,m,k,n进行预测，达到动态控制，既保证测量精度，又保证了信号处理的快速性，这里假设平均转速不变或连续变化。

1.5 信号后处理

对于多成分的时域信号，往往只能直观地感知信号的波动情况和峰-峰值信息，为了更准确地获知信号成分信息，常常需要做频谱分析。信号在进行时频转换时，通常在快速傅里叶变换(fast Fourier transformation,简称FFT)之前的加窗处理会不可避免地带来能量泄露[10]，信号幅值会出现一定的误差，这对扭振信号的分析是不利的。笔者使用3点卷积幅值校正法[11]对信号进行处理。

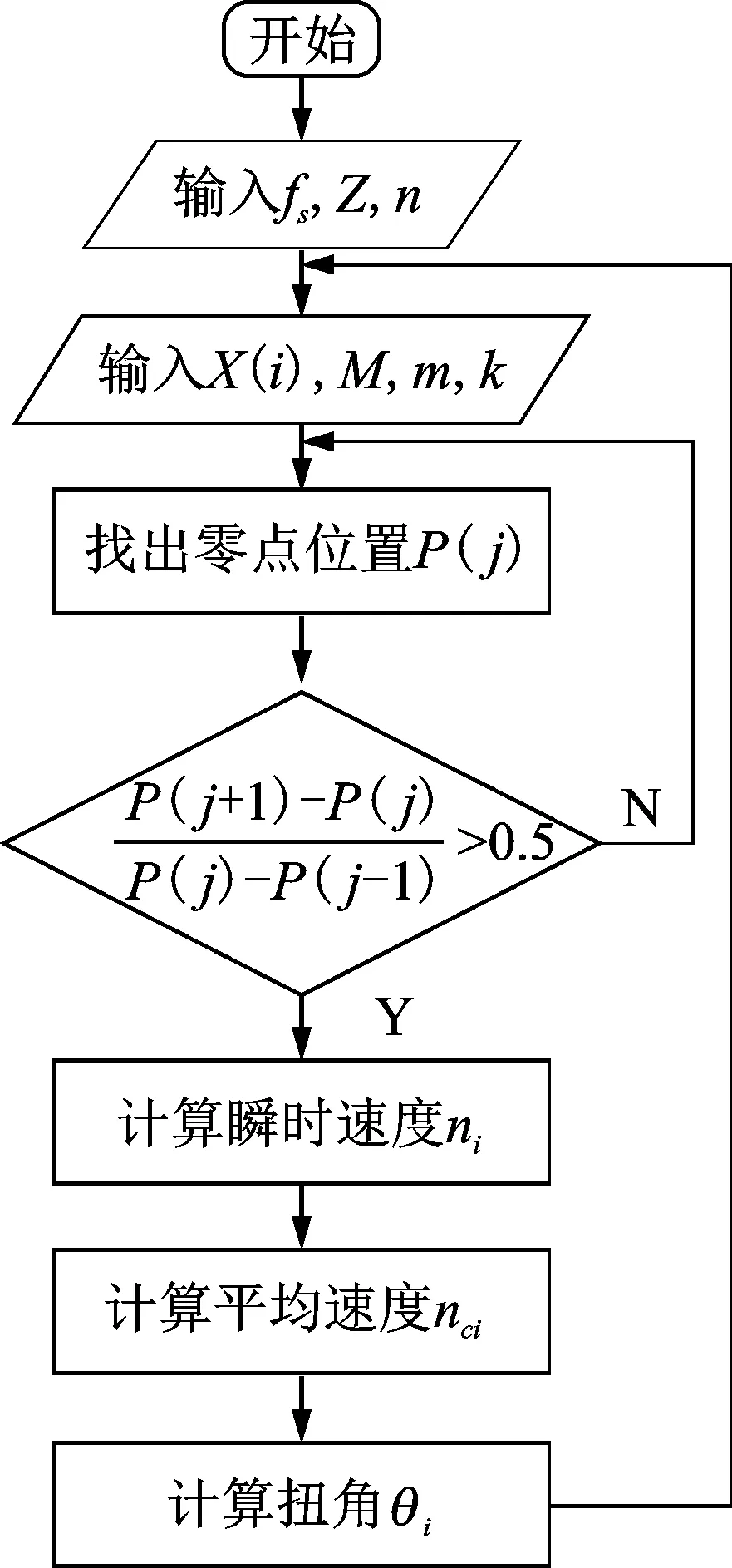
图4 基于高频采样的扭振信息提取算法流程图Fig.4 Flow chart of extraction algorithm for torsional vibration based on high frequency sampling

设Yi为加hanning窗后的频谱幅值，Kt为hanning窗的恢复系数，对hanning窗取为8/3。其3点卷积幅值校正公式[11]为

(15)

理论上，加hanning窗进行时频转换引起的幅值误差由15.3%降到1%以下。

提取到的扭振信号等效为等角度采样得到的数字信号，轴系旋转一周相当于采集测速齿盘的齿数个数据。但FFT计算一般要求采样点数为2的整数次幂(考虑到算法易实现性)，此处采用在采样数据的基础上进行3次样条插值进而进行2次采样的方法得到所需数据点数。

1.6 该系统的误差分析

虽然在算法上引入了周期平均和齿平均来降低因转速波动和齿的分度误差所带来的噪声，但还不能做到完全消除；由弯扭耦合引入的误差可以通过对称安装传感器的办法进行减弱，但由于此项误差很微弱，很难保证传感器的绝对对称，可以不予考虑；由传感器偏心产生的噪声振幅不变，谐次永远为1次；转速波动产生的噪声信号谐次较低，一般不高于2次，在低速区较为严重；轴系滚振的谐次一般不高于4次，且随转速的升高，由此产生的影响减小。

由以上分析可知，在进行扭振信号分析时，前几个谐次的幅值误差较大，这在以往的测试系统当中也存在。所以在本系统和其他测试系统结果进行比对时，由于处理方法的不同，前几个谐次可能差别较大。一般由于外载变化引起的轴系扭振有用信息在4～12谐次内，所以以往的测试系统也都关心这个区段的精度。

2 仿真信号分析

2.1 Matlab信号仿真

构造一个信号，轮流输出15个f1=1 530 Hz和15个f2=1 470 Hz的正弦波信号，模拟30个齿的齿轮输出的平均转速为3 kr/min(其前半周较快为3 060 r/min，后半周较慢为2 940 r/min)的扭振信号。采样频率为32.768kHz，采样时间为2s。模拟信号的放大图如图5所示。

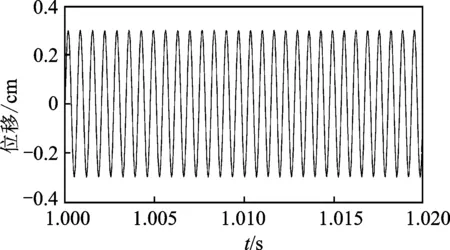
图5 模拟扭振信号Fig.5 The wave of simulated torsional vibration signal

将其积分后，得到的扭角位移信号为一个三角波形的扭角信号[1]，扭振信号的基频为50Hz，扭角幅度由式(16)可得为3.6°(峰-峰值)，振幅为1.8°。根据三角波形的周期函数的傅里叶展开式计算可得1次谐波幅值为1.458，3次谐波幅值0.162，5次谐波幅值为0.058 3。

(16)

将模拟信号经过本研究系统方法处理后，结果如图6～图8所示。

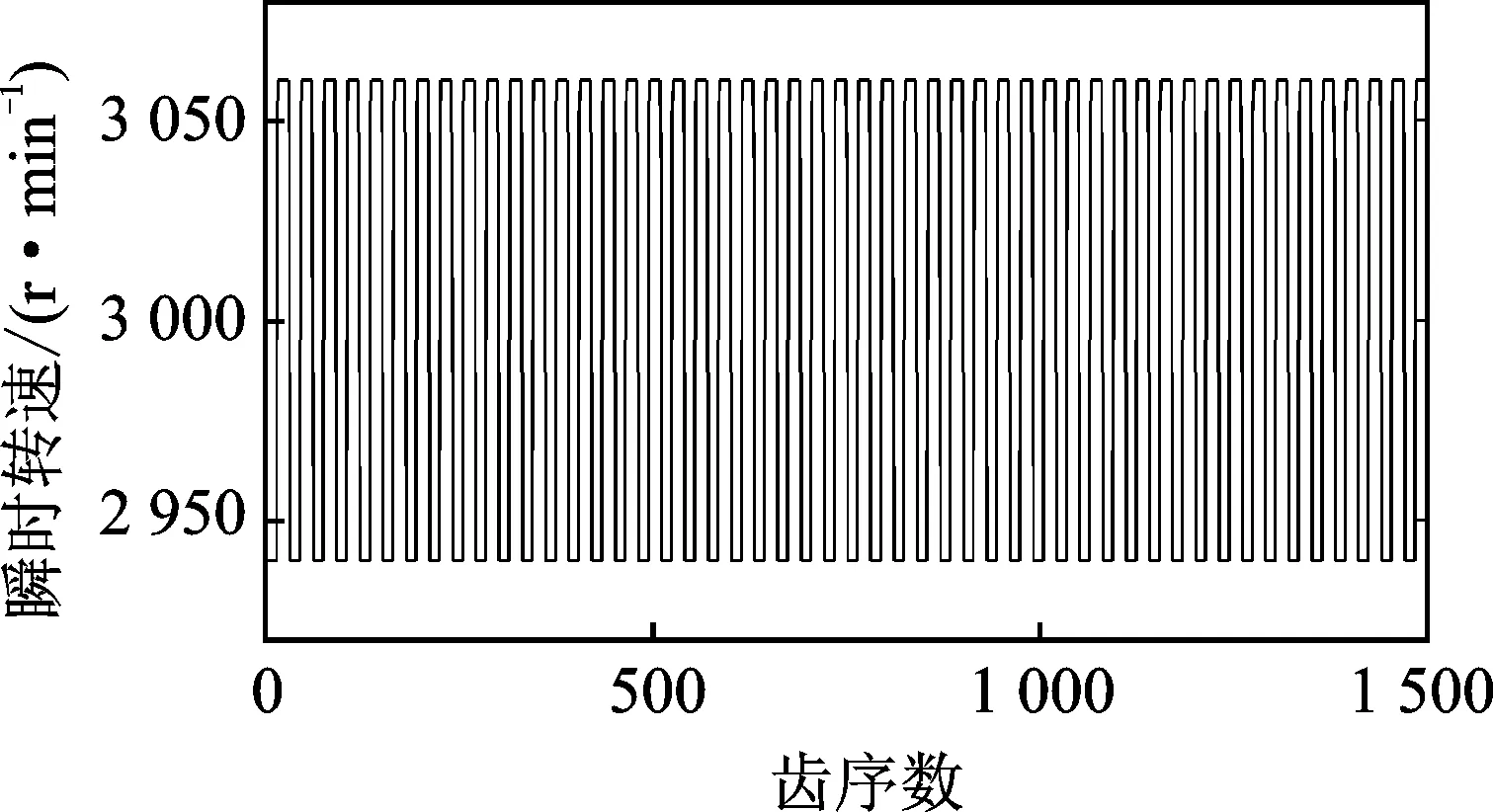
图6 模拟信号瞬时转速Fig.6 The wave of instantaneous speed of simulated signal

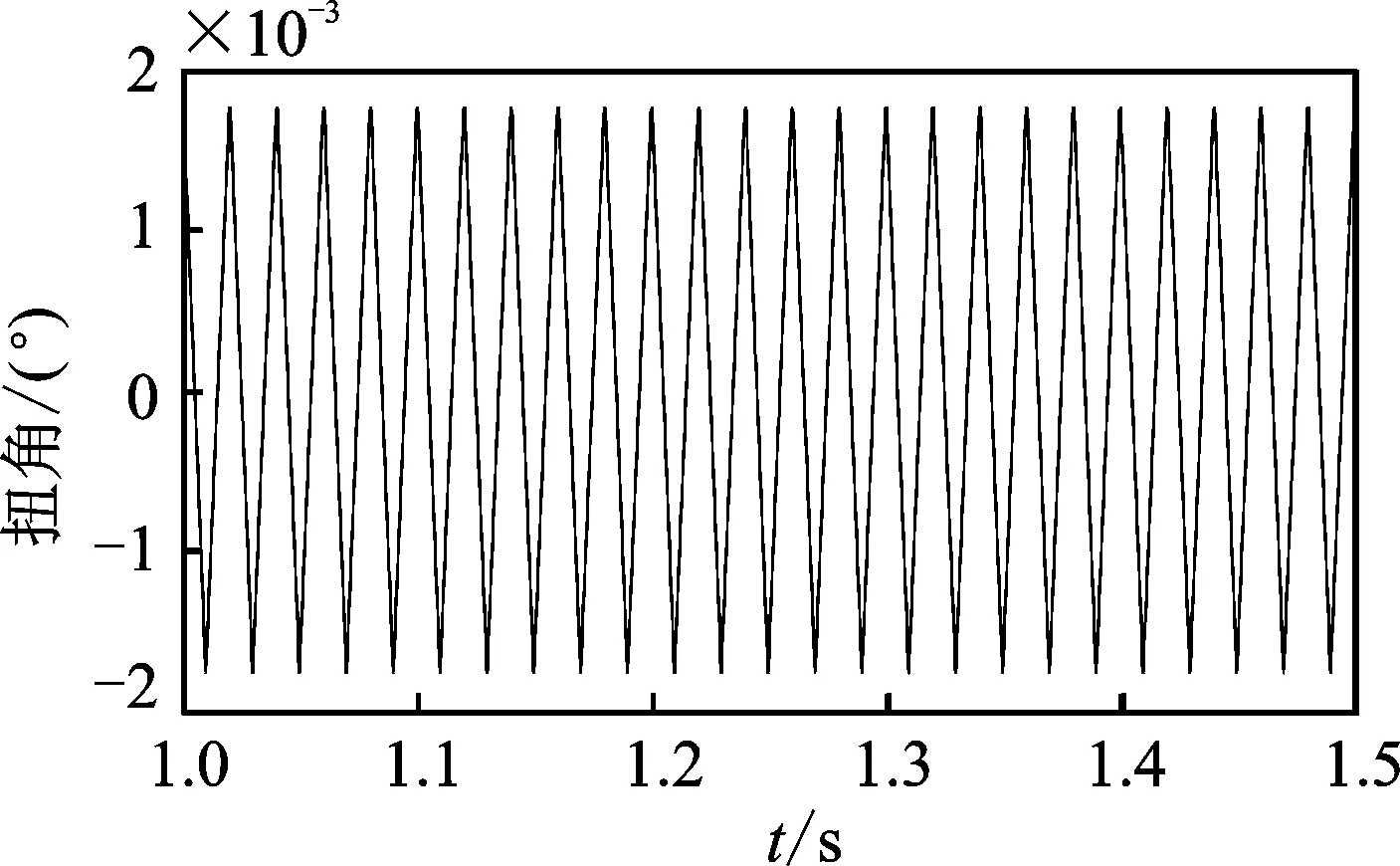
图7 模拟扭振信号时域波形Fig.7 Time domain waveform of simulated torsional vibration signal

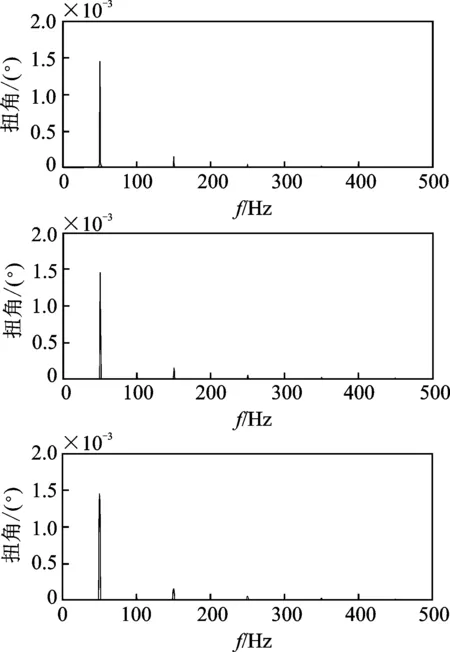
图8 模拟扭振信号频谱图Fig.8 Spectrum of simulated torsional vibration signal

由图6可知，模拟信号的瞬时转速在3 kr/min上下波动，很好地反映了预期结果。图7显示该扭振信号为三角波形，振幅为1.766°，与理论值有一定误差，考虑为数字采样带来的显示误差，这在频谱图上可得到验证。图8为扭振信号频谱图，由上到下依次为直接FFT的频谱分析结果、加hanning窗考虑恢复系数的频谱分析结果，以及应用加hanning窗的3点卷积幅值校正方法得到的频谱分析结果。由图可以看出，频率结果没有误差，各次谐波幅值结果如表1所示。由表1数据可知，3点卷积幅值校正的结果优于前两种方法，得到的幅值结果误差很小，绝对误差在0.1毫度级。

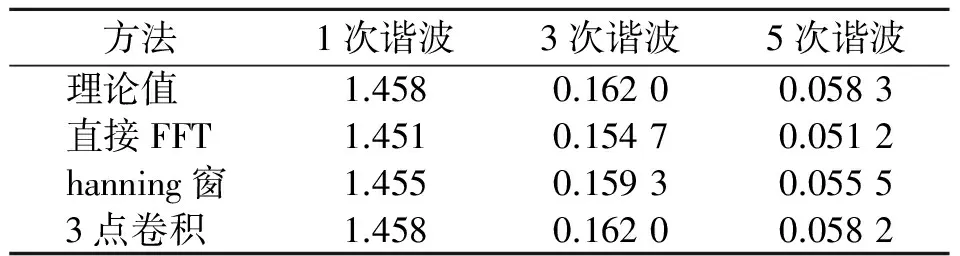
表 1 3种方法的幅值对比

2.2 标定器信号仿真

为提高该方法的可信度，使用该系统对由美国亚特兰大科仪公司生产的扭振标定器产生的扭振模拟信号进行处理分析，该标定器轮流输出50个5 kHz和50个5 063.3 Hz的方波脉冲。模拟具有100个齿的齿轮输出前半周较慢、后半周较快的扭振信号，其平均转速为3 018r/min，基频为50.3Hz，扭角幅度为0.566°，信号采样频率设置为25.6 kHz。处理结果如图9～图12所示。图9显示模拟方波信号噪声较大，图10显示瞬时转速围绕平均转速波动，且瞬时转速也有小幅波动，此为原始信号中的噪声引起。图11显示扭振信号时域波形峰值为0.567 4°，与理论值有一定误差。由表2数据可知，频谱分析结果显示幅值绝对误差在0.1毫度级，频率偏差0.2Hz，精度很高。

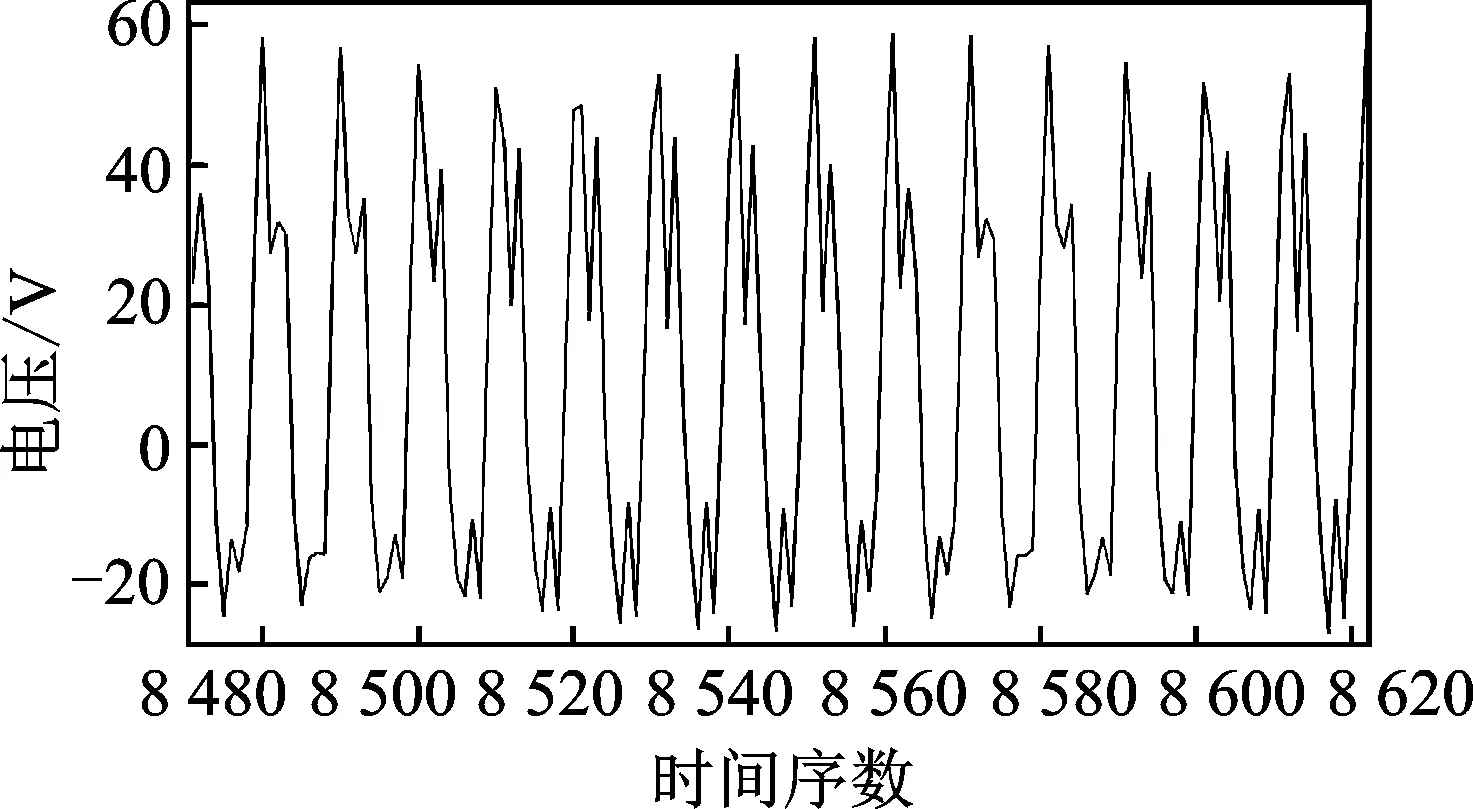
图9 原始信号Fig.9 The wave of original signal

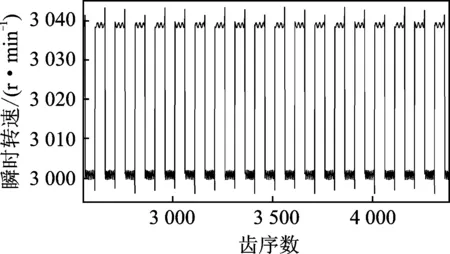
图10 瞬时转速Fig.10 The wave of instantaneous speed

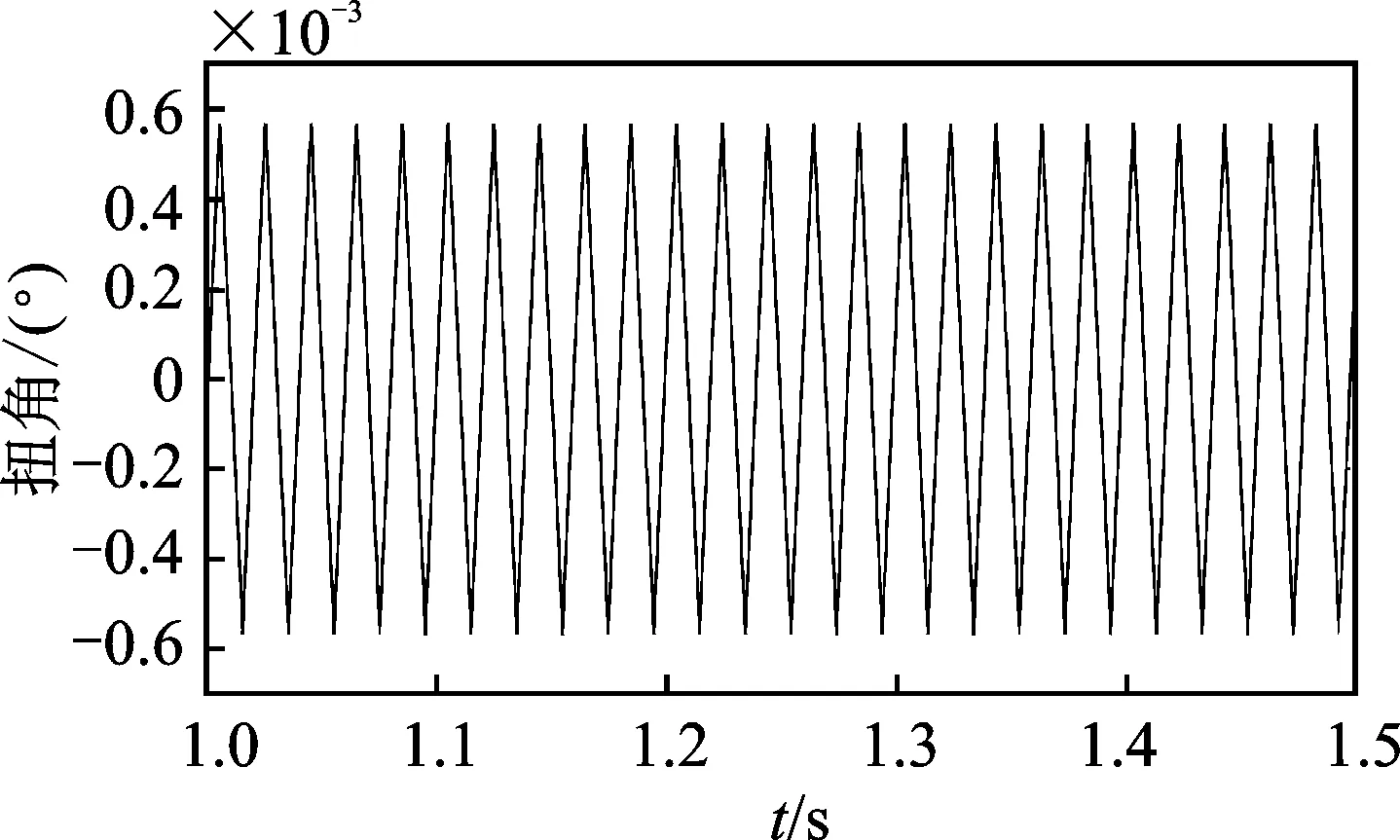
图11 扭振信号时域波形Fig.11 Time domain waveform of torsional vibration signal

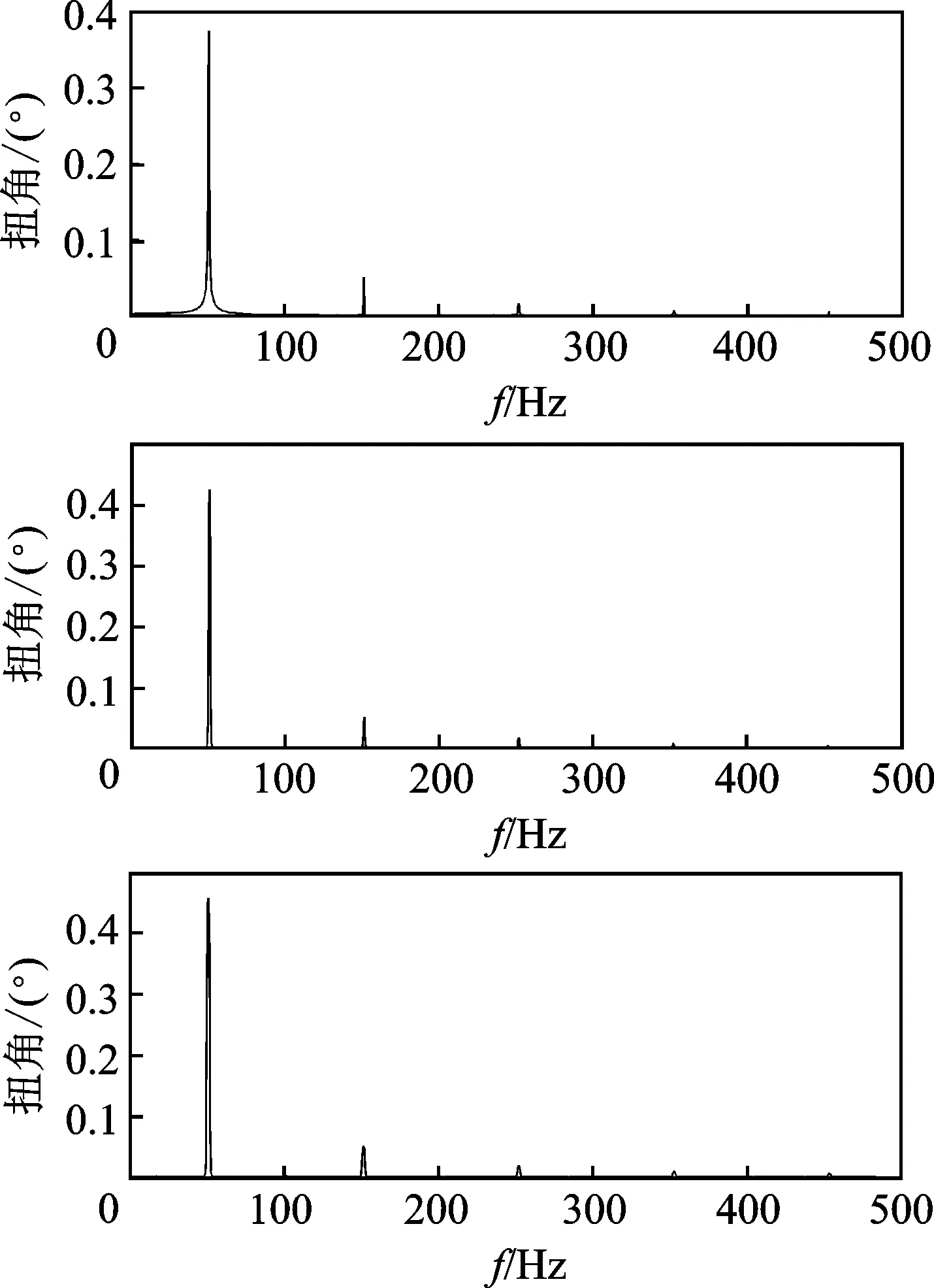
图12 扭振信号频谱图Fig.12 Spectrum of torsional vibration signal

3 实例分析

现场测试中采用加工有30齿的测速齿盘，安装于待测轴合适位置，由MP963扭振磁电传感器采集扭振信息，KMT D2/16数据记录仪记录传感器的采集信号。在实验室将记录仪的信号经CompactDAQ NI9229数据采集器采集(设定采样频率为25600Hz)，输入到该方法实现的程序中处理，分析结果如图13所示。此外将数据记录仪的信号输入到NZ-T扭振分析系统，分析结果如图14所示。

图13 本研究方法扭振分析结果Fig.13 Analysis result of torsional vibration via the proposed method

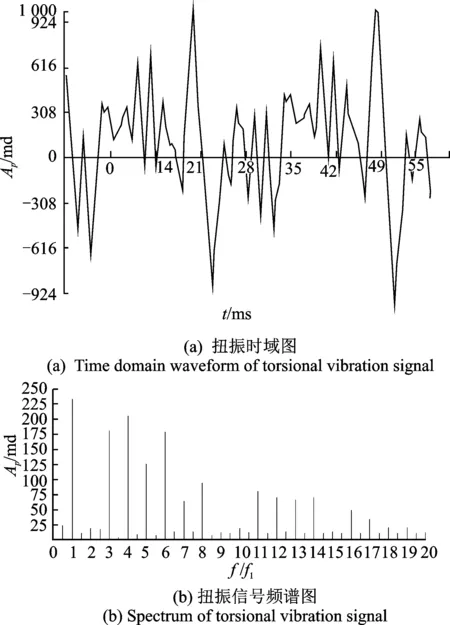
图14 NZ-T分析仪扭振分析结果Fig.14 Analysis result of torsional vibration via the NZ-T type analyzer

将本研究扭振分析方法应用于某船正常航行时的轴系扭振信号分析中，实验结果与NZ-T型扭振分析仪分析结果对比见表3(仅列出部分信息，其他对比可由频谱图观察)。从表3及频谱图分布可以看出，两种方法对基频的识别几乎没有误差，说明频率误差很低；频谱上2次谐波处幅值差别较大，这属外界干扰带来的噪声，说明该结果具有可信度。

表3 两种方法结果对比

4 结 论

1) 笔者构造的基于高频采样法的轴系扭振测试方法经过实验部分结果得以验证，该分析方法和以往扭振分析仪相比，都达到很高的精度，结果具有可信度。

2) 该系统实现了扭振分析仪硬件部分的简化，具有通用性，为弯振、扭振、横振等振动信号的联合测试奠定了基础，同时也为以后的扭振测试节省了成本。

3) 分析过程说明，3点卷积幅值校正方法对控制能量泄露、得到精确幅值起到了很大作用。

[1] 杜极生. 轴系扭转振动的试验、监测和仪器[M].南京：东南大学出版社,1994:1-4.

[2] 许楚镇, 张恒涛. 汽轮发电机组轴系扭振事故剖析和技术开发展望[J]. 动力工程学报, 1990,10(2):9-14.

Xu Chuzhen, Zhang Hengtao. Analysis of shaft torsional vibration of steam turbine generator unit and prospect of technology development [J].Power Engineering,1990,10(2):9-14.(in Chinese)

[3] 郭力, 李波. 轴系扭转振动测量方法评述[J]. 精密制造与自动化, 2000(3):53-56.

Guo Li, Li Bo. Measurement method of torsional vibration of shaft system [J]. Precise Manufacturing & Automation, 2000 (3): 53-56. (in Chinese)

[4] 杨卓君, 廖明夫. 基于加速度传感器测量扭振方法的研究[J]. 噪声与振动控制, 2008, 28(5):163-167.

Yang Zhuojun, Liao Mingfu. Research on torsional vibration method based on acceleration sensor [J]. Noise and Vibration Control, 2008,28 (5):163-167. (in Chinese)

[5] 李松和, 俞小莉, 周迅,等. 内燃机扭振数字化测试系统及其应用[J]. 车用发动机, 2005(2):52-53.

Li Songhe, Yu Xiaoli, Zhou Xun,et al. Digital test system for torsional vibration of internal combustion engine and its application [J]. Vehicle Engine, 2005 (2): 52-53. (in Chinese)

[6] 杜极生. 国内外关于扭振监测装置的研究综述[J]. 汽轮机技术, 1991(5):16-19.

Du Jisheng. A review of the research on torsional vibration monitoring device at home and abroad [J].Steam Turbine Technology, 1991(5):16-19. (in Chinese)

[7] 董大伟, 闫兵, 谭达明. PC仪器扭振测量系统[J]. 仪表技术与传感器, 2001(12):18-19.

Dong Dawei, Yan Bing, Tan Daming. The torsional vibration measurement system of PC instruments[J]. Instruments and Meters, 2001(12):18-19. (in Chinese)

[8] 蒋云帆, 廖明夫, 王四季. 航空发动机转子扭振测量新方法[J]. 振动、测试与诊断, 2013, 33(3):411-415.

Jiang Yunfan, Liao Mingfu, Wang Siji. A new method for measuring torsional vibration of aero engine rotor[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(3): 411-415.(in Chinese)

[9] 张晓玲, 唐锡宽. 转轴扭角及扭振测试技术研究[J].清华大学学报:自然科学版, 1997(8):83-86.

Zhang Xiaoling, Tang Xikuan. Shaft torsional angle and torsional vibration test technology research[J]. Journal of Tsinghua University:Natural Science Edition, 1997 (8):83-86.(in Chinese)

[10] 蒋毅, 古天祥. 一种修正的FFT高精度谐波分析方法[J]. 电子测量与仪器学报, 2006, 20(1):19-21.

Jiang Yi, Gu Tianxiang. A novel way ofimproving harmonic analysis precision based on amending FFT[J]. Journal of Electronic Measurement and lnstrument, 2006, 20(1): 19-21.(in Chinese)

[11] 丁康, 谢明，王志杰. 离散频谱的幅值,相位和频率的校正方法及误差分析[J]. 动态分析与测试技术, 1996(1):10-29.

Ding Kang, Xie Ming, Wang Zhijie. Correction method and error analysis of amplitude, phase and frequency of discrete spectrum[J]. Dynamic Analysis and Testing Technology, 1996 (1): 10-29.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.002

国家科技支撑计划资助项目(5015BAF07B03)；上海市创新行动计划资助项目(15JC1402600)

2016-03-15；

2016-05-23

TH133.3； TH165.3

郭文新，男，1990年4月生，博士生。主要研究方向为结构健康监测与故障诊断、转子动力学。

E-mail:guowenxin1990@sjtu.edu.cn