储能超级电容动态响应优化自适应控制策略
陈 威 叶少士 刘 冬
(1. 浙江网新联合工程有限公司,杭州 310051;2. 诺基亚通信系统技术有限公司,杭州 310053)
储能超级电容动态响应优化自适应控制策略
陈 威1叶少士2刘 冬1
(1. 浙江网新联合工程有限公司,杭州 310051;2. 诺基亚通信系统技术有限公司,杭州 310053)
微电网储能系统中的超级电容器组主要用于满足系统对快速动态响应的要求,因此其在不同工况下的响应需要保持一致性,以保证后级用电负荷的匹配度。本文提出了一种以动态响应一致性为最优目标的自适应控制策略。根据系统的小信号模型,在保持稳定性的前提下,可借助系统的阶跃响应分别求出不同工作状态下的合适控制参数。在运行时,即可根据系统当前所处的工作状况,由微处理器在线自动选择最优的控制参数组合,从而达到任何情况下的输出动态响应一致化。在给出了原理分析和设计方法后,实验样机证明了该新颖自适应控制策略的有效性,具有应用价值。
超级电容;动态响应;控制策略
作为可再生清洁能源技术的典型应用,微电网将在未来智慧城市供能、交通以及保障工商业活动等各项主要市政功能建设中起到支撑作用,在我国已被列入“十三五”相关规划。为了保证微电网稳定可靠运行,其内部的储能系统需要兼具高能量密度和高功率密度的特性,以抑制负荷突变带来的功率波动,并改善电能质量[1-5]。该储能系统一般采用电池组和超级电容器两种储能元件混合的形式,其中电池组可满足高能量密度要求,维持稳态母线电压;而超级电容器可改善系统动态响应,缓冲负荷波动带来的功率冲击,延长储能装置寿命[6-8]。超级电容器组通常是经过后级 DC-DC变流器实现和母线间的功率和能量传递。在设计上,超级电容器组的端压在充放电的过程中一直处于变化状态,不会保持相对恒定,这就对后级的变流器的控制带来了挑战:因该变流器的主功率增益中包含超级电容器端压 VUC项,故变流器输出的暂态过程特征也是随VUC变化的[9],很难通过一套固定的PI或PID反馈环节参数加以优化。而这些随外部条件变化的超调量及调整时间等动态响应指标,不利于后级用电负荷的匹配设计。在极端情况下,易造成储能系统和负荷之间的时序失配或电压超限,影响微电网的稳定运行,并降低可靠性。
本文提出的新颖自适应控制方案,以保证在各种条件下 DC-DC变流器的输出动态响应特征一致性为优化目标,通过检测输入输出状态,在线选取适应的控制参数,从而实现输出动态响应和变流器外部工作状况解耦,便于后级用电负荷的电气配合。
1 传统固定系数控制策略
图1给出了一个超级电容器组和后级双向DCDC变流器组成的经典储能单元,用电负荷用等效电阻RL代替。一般而言,微电网实际运行时,超级电容器组需要快速补偿负荷功率扰动,因而图1所示的变流器工作在boost模式下的动态响应更为重要,此时超级电容器组为放电模式。该工作状态下的系统小信号简化模型如图2所示,由电流内环和电压外环组成。其中,Hvd(s)为经典 PI反馈环节传函,Gi为电流内环等效传函,Gp(s)为主功率传函。电流内环的动态响应(带宽大于 10kHz)远大于电压外环,为了简化分析,将Gi等效为单位增益[10]。根据文献[10],Gp(s)可表示为

图1 超级电容器组储能单元
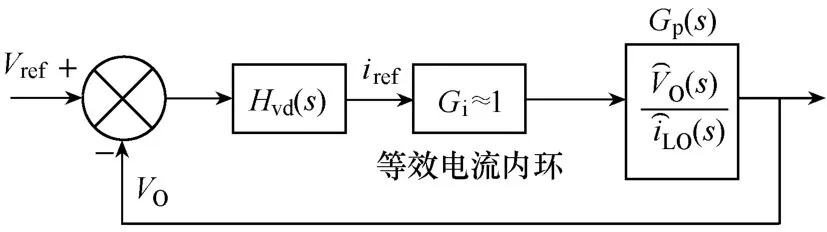
图2 系统简化小信号模型

式中,VO为负荷端压;Lf为变流器输入电感感量;CO为输出电容。设
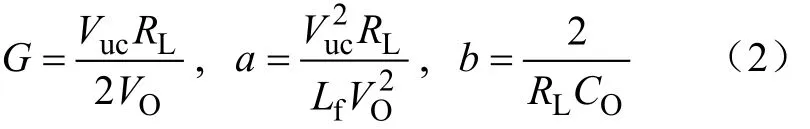
则Gp(s)可表示为
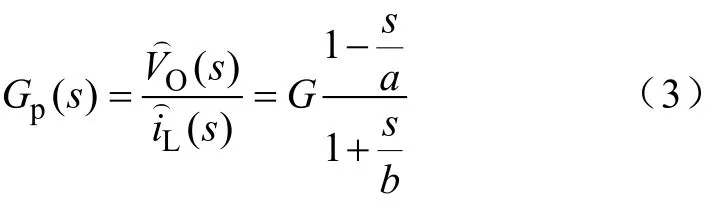
可得系统开环传递函数GO(s)为

式中,Kp为比例系数;Ki为积分系数。根据图2和式(4),可得系统闭环传函GC(s)为
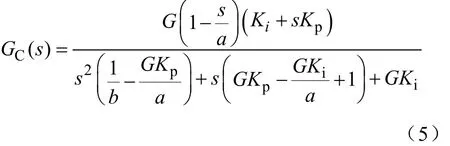
根据劳斯判据,需要式(5)分母的两个系数项均大于零才能保证稳定,经过化简,可得此时 Kp和Ki的上限Kps和Kis分别为

此时命题变为系统在满足式(6)条件下的 Kp和 Ki取值。显见式(5)是典型二阶系统,代入阻尼系数ξ,则由文献[11]可知
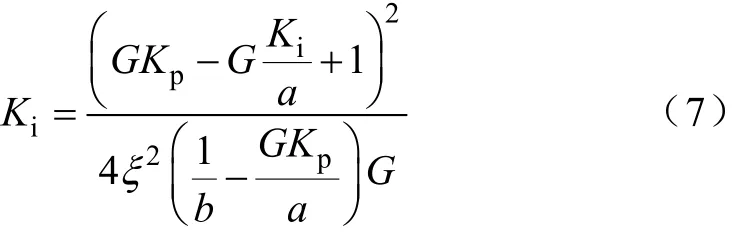
取ξ =0.707,式(7)的有效解为
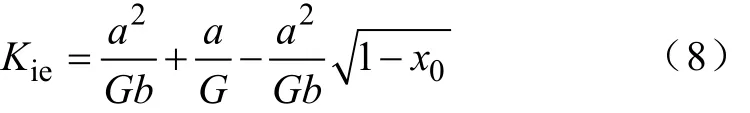
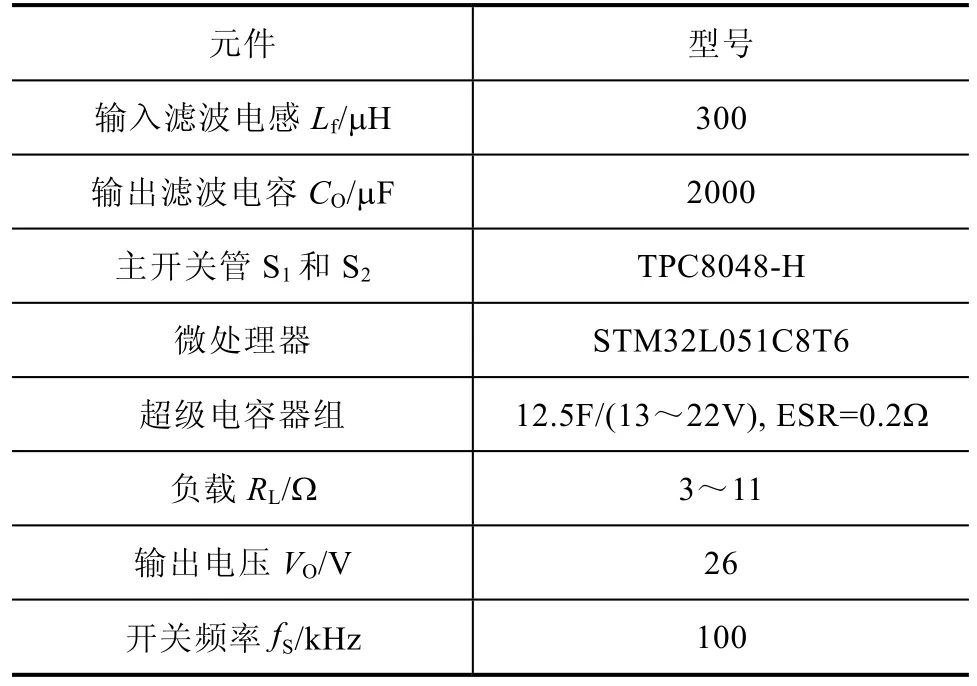
表1 主要器件参数
可取Kp=1.4和Ki=600(Kps=10.5,Kis=28330)为例进行系统阶跃响应仿真,如图3所示。

图3 固定反馈参数下的阶跃响应仿真
从图3可见,对于不同输入电压下的输出阶跃响应表现也不同,输出电压超调量和调整时间等指标在输入电压 VUC的上下限时相差较多。可以预计在超级电容器组的暂态放电过程中,输出电压的下冲量也是不恒定的,因而如前文所述,为后级的负荷用电设备的匹配性设计造成了一定难度。
2 系数可变自适应控制策略
若控制系统参数可根据变流器的当前输入输出状况动态可变,则在理论上可以让各种情况下的变流器动态响应变得基本一致,达到预期所需。下面是这一思路的具体阐述。
2.1 可变比例系数Kp的设计
在满足式(6)的前提下,Kp的优化选值可根据系统在不同情况时的动态响应求得。在理想状态下,系统的阶跃响应可认为由Kp起主导作用,此时系统外环的部分控制如图4所示。
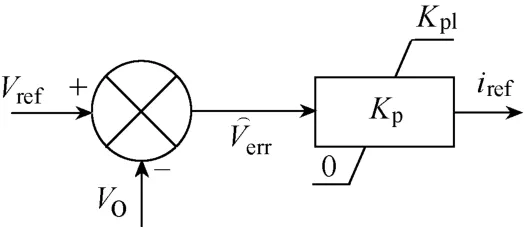
图4 部分外环控制框图
其中,Kp在不同外界情况下可在[0, Kpl]范围中任意取值,以达到当前情况下的最优。Vref为电压外环基准,为电压比较误差,iref为电流内环基准。由图4可得

由能量守恒 irefVuc=/RL,从式(9)可得


对上式施加拉氏反变换,对应时域函数为
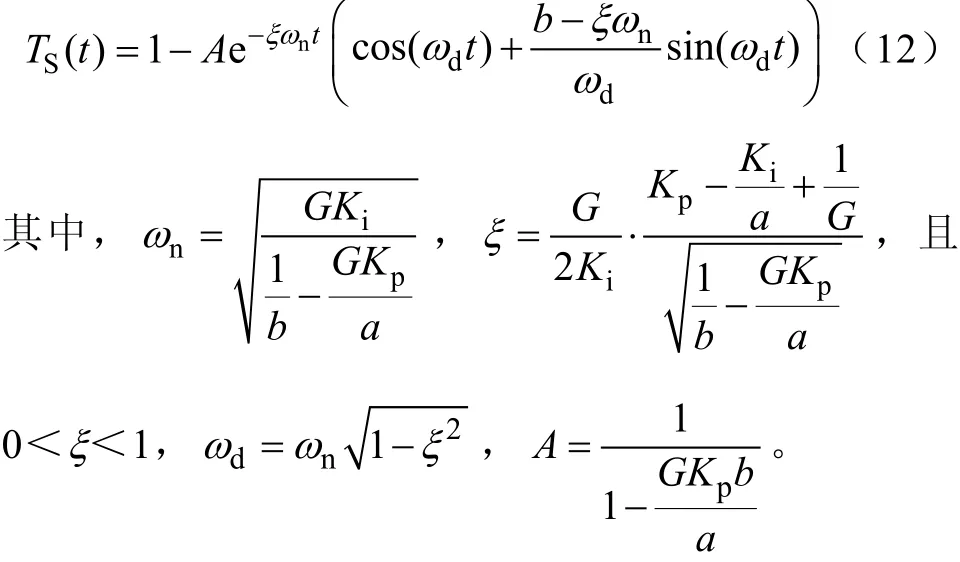
则可求出当ξ =0.707时的系统过冲量 TSO:令dTS(t)/dt=0,求出过冲最大时对应时刻后反代入式(12),可得

同时,由系统右半平面零点引起的电压下跌量TSU为

根据式(13)和式(14),可以分别绘制出参数在各种工况下的系统响应特征曲线,见表 1。如果选取阶跃响应的电压超调量和下跌量均为20%,则通过图形查找法可知 Kpl为2.5(Kps仍为 10.5)。进而通过类似的查图形方式,可得不同外界条件下的最优化Kp表格,见表2。因其过程较为繁琐,在此从略。

表2 不同条件下的最优化Kp取值
可看出表2中Kp所有取值均满足式(6)。
2.2 可变积分系数Ki的设计
在 x0<<1的情况下,可将式(8)按照泰勒级数展开,并取其前两项反代入式(8)可得出 Kie的近似值Kia为

类似地,由上式也可得出当ξ =0.707时各种不同外界条件下的Ki最优值表格,见表3。

表3 不同条件下的最优化Ki取值
同样地,上述表中所有Ki的取值均满足式(6)之稳定性上限条件。
将式(10)代入式(15),即可得系统电压外环的完整控制框图,如图5所示。
根据上述分析,对所提出的自适应控制策略进行了系统阶跃仿真,所得结果如图6所示。可见由于采取了对不同工作条件下的优化取值,所有阶跃响应的曲线和相关性能参数特性基本保持一致,达到了预期的设计目的。
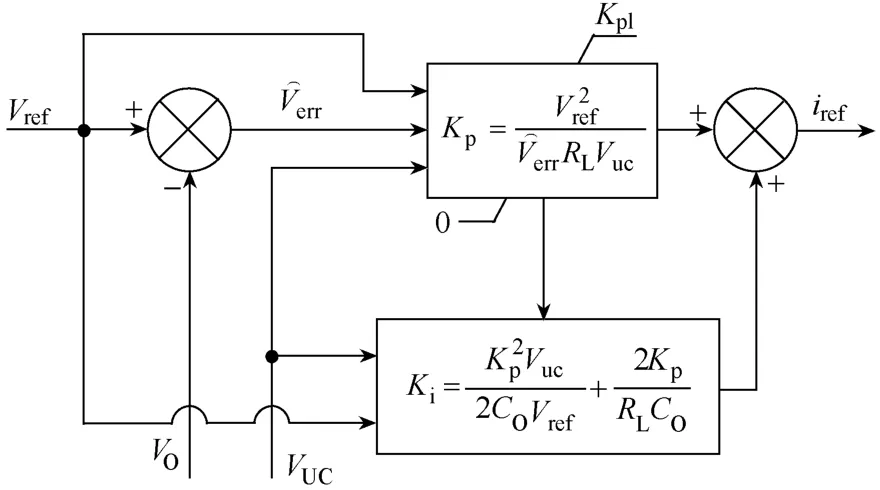
图5 完整电压外环控制框图

图6 自适应反馈参数的阶跃响应仿真
在实际中,控制变流器的微处理器根据外界条件采样结果,在线运算相应的Kp和Ki。或通过更为简单的查表方式,动态选择与当前工作状况最为接近的上述两个参数,在工程中可以达到和实时运算相近的效果,计算量和实时性可大为改善。
3 实验结果
为了验证本文所提方法的有效性,按图1和表1的参数构建了一台样机,并施加本文所提自适应控制策略,测试其在不同放电条件下的输出动态响应波形,负载 RL为 11Ω。实验条件为双向 DC-DC变流器从初始的对超级电容器组进行恒流充电状态,快速切换到反向放电状态,以模拟母线功率扰动。实验结果如图7所示。可见在不同VUC输入条件下(a:16V,b:19V和 c:22V),输出电压 VO的动态响应特性基本保持一致,且调节时间也均为12ms左右,与理论效果吻合。为了进行对比,图8是施加固定参数 Kp=1.4和 Ki=600时,在不同 VUC输入条件下(a:16V和b:19V)的对比实验波形。可见VO输出波形在低压输入时下跌略多,且调整时间也较长。对比图 7和图 8,证明了所提自适应控制策略的可行性和有效性。
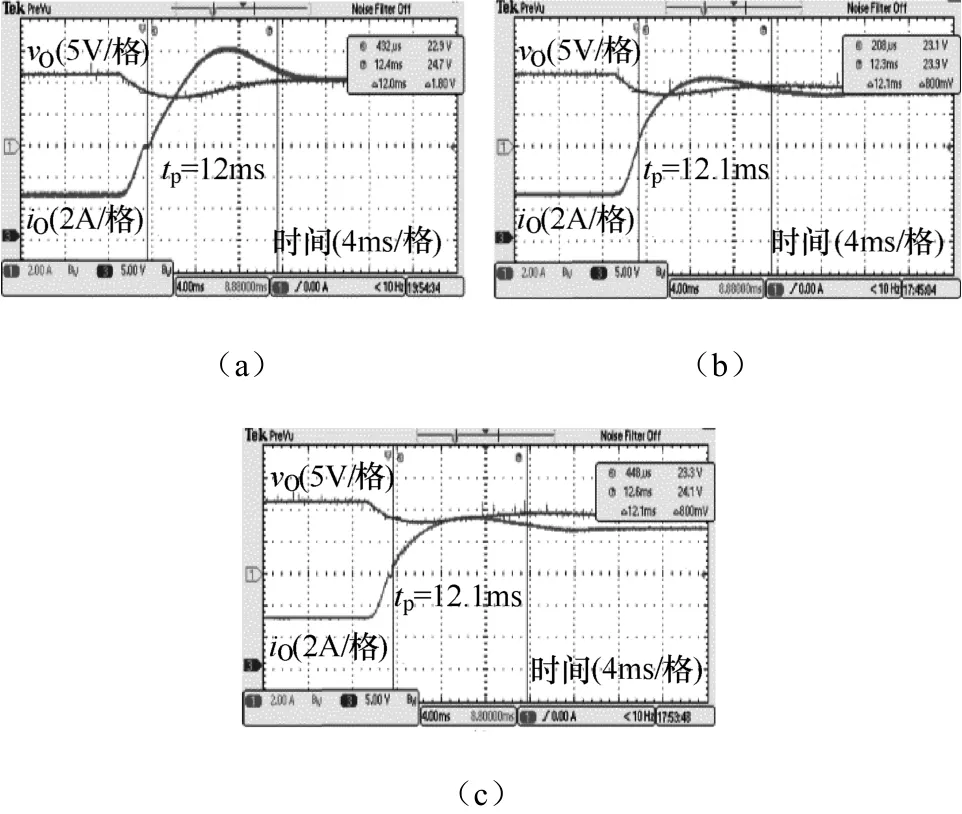
图7 自适应控制策略的实验波形
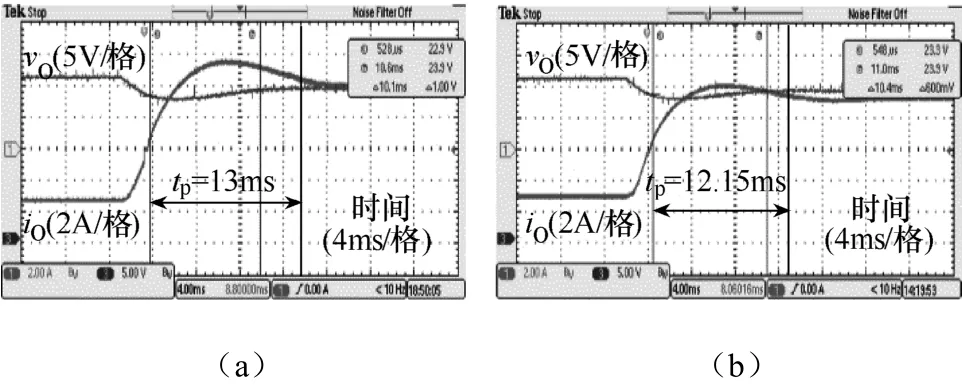
图8 固定参数控制的实验对比波形
4 结论
本文提出一种针对储能系统中超级电容器组动态响应一致性最优的自适应控制策略。通过系统的小信号模型,以各种情况下的阶跃响应一致性为目标,可求得当前工作条件下最优化的控制参数。经由微处理器根据实际情况加以动态选择上述控制参数,达到输出动态响应一致的设计目的,以简化后级负荷的设计难度,增加系统匹配性。实验样机和结果证明了自适应控制策略的正确性和所提控制策略的可行性,具有实际应用价值。
[1] 周林, 黄勇, 郭珂. 微电网储能技术研究综述[J]. 电力系统保护与控制, 2011, 39(7): 147-152.
[2] 张明, 朴政国. 含储能的分布式光伏并网系统对配电网调峰的研究[J]. 电气技术, 2016, 17(12): 11-14,19.
[3] 韩腾飞, 杨明发. 基于双模 MPPT控制的光伏充电设计[J]. 电气技术, 2017, 10(4): 49-55.
[4] 马丽洁, 廖文江, 高宗余. 城轨列车车载超级电容储能控制策略研究[J]. 电工技术学报, 2015, 30(S1):63-68.
[5] 徐从启, 贾桂芝, 李祖贤, 等. 考虑多能量流的光柴储独立微电网协调控制[J]. 电气技术, 2017, 18(4):61-65.
[6] 李武华, 徐驰, 禹红斌, 等. 直流微网系统中混合储能分频协调控制策略[J]. 电工技术学报, 2016,31(14): 84-92.
[7] 程志江, 李永东, 谢永流, 等. 带超级电容的光伏发电微网系统混合储能控制策略[J]. 电网技术, 2015,39(10): 2739-2745.
[8] 赵亚杰, 夏欢, 王俊兴, 等. 基于动态阈值调节的城轨交通超级电容储能系统控制策略研究[J]. 电工技术学报, 2015, 30(14): 427-433.
[9] Jing W, Lai C H, Wong S H W, et al. Batterysupercapacitor hybrid energy storage system in standalone DC microgrids: areview[J]. IET Renewable Power Generation, 2016, 11(4): 461-469.
[10] Leyva-Ramos J, Morales-Saldana J A. A design criteria for the current gain in current-programmed regulators[J]. IEEE Transactions on Industrial Electronics, 1998, 45(4): 568-573.
[11] Erickson R W, Maksimovic D. Fundamentals of Power Electronics 2nd ed[M]. US: Springer, 2001.
Adaptive Control Strategy for Optimum Transient Response of Energy Storage Supercapacitor
Chen Wei1Ye Shaoshi2Liu Dong1
(1. Zhejiang Insigma United Engineering Co., Ltd, Hangzhou 310051;2. Nokia Networks, Hangzhou 310053)
Supercapacitor is utilized to provide fast dynamic response for the energy storage system in micro grid application, which requires the output transient response ought to be identical to ease the design of downstream load by decrease the dependence of electrical spec matching. To fulfill that requirement, this paper proposes a novel adaptive control strategy aiming at having the same transient response for the output of the converter. The most suitable control parameters are calculated under different operation conditions based on the step response characteristic, which is through the modeling of the system and under the safety of stable operation. The MCU can online select the proper combinations of control parameters corresponding to the condition that the converter is currently working under with, to maintain a same output transient response under all conditions. The detail operation principles, as well as the design considerations, were presented. A prototype was built to verify the validity and applicability of this proposed adaptive control strategy, thus proves its engineering value for industrial practice.
supercapacitor; transient response; control strategy
国家高技术研究发展计划项目(863 计划)(2013AA03A117)
陈 威(1982-),男,浙江杭州人,博士,工程师,现从事电力电子拓扑、高可靠性LED驱动技术、智慧城市分布式微电网系统的研究工作。

