利用多目标最优化方法控制智能电网中电动汽车充电速率

关昊亮 王进华 邱伟育

（1. 福州大学电气工程与自动化学院，福州 350000；2. 台湾元智大学电机工程学系，台湾 桃园 32003）

利用多目标最优化方法控制智能电网中电动汽车充电速率

关昊亮1王进华1邱伟育2

（1. 福州大学电气工程与自动化学院，福州 350000；2. 台湾元智大学电机工程学系，台湾 桃园 32003）

本文考虑智能电网中家用电动汽车和电动出租车的充电调度问题。充电站可以控制充电速率以最大化其收入；对于底层电力系统，期望最大化其自身的负载因子，从而确保系统的稳定性。充电站最大化其收入与电力系统最大化其负载因子形成一个多目标优化问题。本文提出多目标最优化方法来解决此多目标优化问题，进而产生柏雷多（Pareto）最优电动汽车充电策略。文末进行数值分析来验证所提出方法的有效性。

智能电网；插电式电动出租车；多目标优化；柏雷多最优

近几年来，随着全球能源危机的不断加深、石油资源的日趋枯竭、空气污染、全球气温上升等危害的加剧，各国政府及汽车企业普遍意识到节约能源和减少有害气体的排放是未来汽车技术发展的必然方向[1]。发展电动汽车是解决上述问题的一条途径[2]，然而大量的电动汽车接入电网会增加电网整体的负担。估计到2050年，中国电动汽车的数量将达到2亿，总充电量将达到3.3亿kW[3]，电动汽车的急剧增加对中国电力供应将造成重要影响。对于不同的电价收取模式，电动汽车会有不同的充电需求，会在不同时段从电网获取电能补给。电网与电动汽车交易模式将渐趋复杂，需要更加先进的电力市场来支撑此变化[4]。随着电动汽车的大规模增长，对于充电站的充电排程与充电速率的研究就显得尤为重要。充电站作为电网系统的运营商，会最先接触到电动汽车用户，可以通过优化充电站各个充电桩的充电速率，来调节各个时段的电网负载，维护电网稳定[5]。

本文分成几个部分探讨相关议题：首先讨论充电站及其服务对象的数学模型，然后介绍智能电网模式下的电价策略，最后探讨相对应的多目标优化问题并提出解决方法。为了展示方便，本文以30min为一个时段（time slot），将一天分为48个时段。

1 充电站及其服务对象的讨论

1.1 充电站规模

充电站在未来社会中的重要性与现在的加油站类似，为了调节充电站各时段的用电负载量，充电站可以调控家用电动汽车的充电速率，充电速率的范围为 5kW/h到 15kW/h。本文所用模拟的充电站规模为每个充电站有20个充电桩，最大可同时负担20辆电动汽车进行充电。在充电站进行充电的电动汽车包括插电式电动出租车（plug-in electric taxi,PET）与家用电动汽车。

1.2 插电式电动出租车

随着电动汽车产业技术的发展，充电站在未来社会中会存在大量的需求。与家用电动汽车相比，插电式电动出租车更希望加快其充电速率，减少充电时间。未来越来越多的营运出租车也将由现在的燃油车变为插电式电动出租车，公共电动汽车将在未来的公共交通中发挥重要作用，充电站也将服务更多的插电式电动出租车。

图1为一个城市内所有电动出租车（共10组车队）每隔 30min充电数量的仿真图[6]。在本文的模拟仿真里，选择其中一组车队进行模拟。为了促进电动出租车的推广并降低其电池的损耗，原则上充电站对于电动出租车的充电速率固定为14kW/h。而且充电站在各个时段必须首先满足电动出租车的充电要求，然后再考虑家用电动汽车的充电要求[7]。

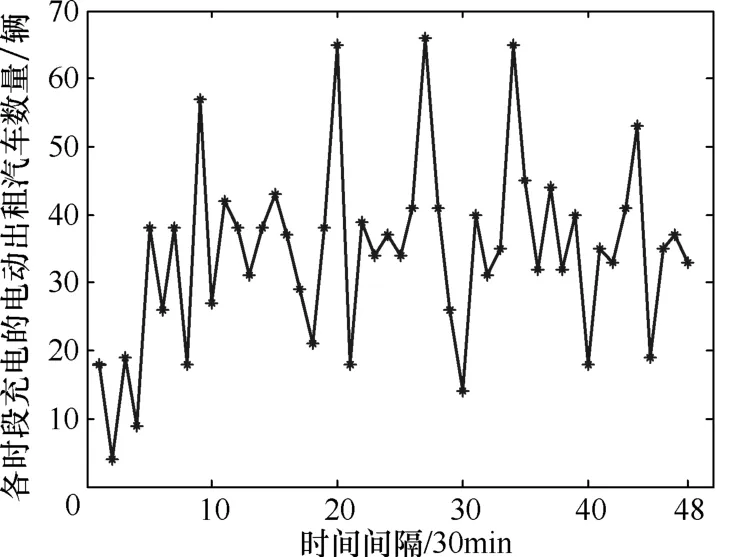
图1 一天各时段接入快速充电站中电动出租车的数量

1.3 家用电动汽车

本文模拟所使用的家用电动汽车，其电池的最大容量全部统一为27kWh。家用电动汽车去充电站充电时，电池的剩余电量可以表示为

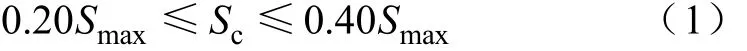
式中，Sc为家用电动汽车进入充电站时电池的剩余电量；Smax为电池的总容量。本文随机模拟 200辆家用电动汽车初始的剩余电量，其范围全部在电池总容量的20%～40%。

由于快速充电技术的发展，充电站可以在短时间里将电动汽车的电池电量提升至85%，之后为保护电池性能，电流就会慢慢下降。因此，当家用电动汽车的电池容量高于电池总容量的85%后，家用电动汽车会在充完这个时段的电量后结束充电。家用电动汽车的充电目标表示为

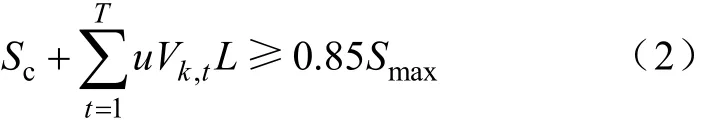
式中，k表示第k台家用电动汽车，k=1,2,…,K，本文设定 K=200；t表示时段，t=1,2,…,T，T=48；u表示充电站给电动汽车充电的充电效率[8]，本文设定为 u=0.9；L表示一个时段的长度，L=0.5h；Vk,t表示家用电动汽车k在t时刻的充电速率。

图2为家用电动汽车一天去充电站充电的可能分布[9]，受规模的限制，充电站最多只能同时负担20辆电动出租车与家用电动汽车充电。当家用电动汽车与电动出租车要求充电的总数大于20辆时，为了推广公共绿色交通，充电站会优先允许电动出租车进行充电。家用电动汽车只能排队等候充电或者选择其他充电站进行充电。

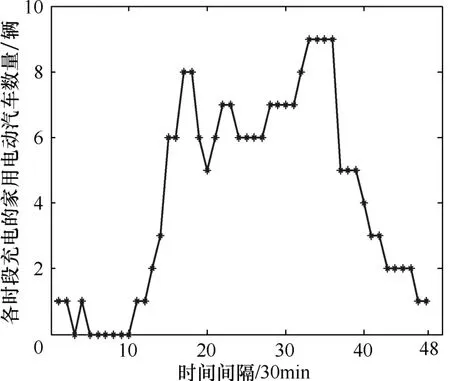
图2 一天各个时段内快速充电站中家用电动车的数量

2 智能电网的电价策略

电网公司会通过改变电价的高低来引导用电者转移高峰用电量，常见的电价模型有：即时电价（Real-time pricing）、前一天公布的电价（Day-ahead pricing）、分时电价（Time-of-use pricing）、尖峰时间反馈电价（Peak-time rebate pricing）等[10-13]。

本文使用美国宾夕法尼亚州新泽西马里兰互联电力公司（PJM）在2017年5月25日公布的价格（前一日公布的电价），其电价系统在高峰时段和离峰时段的单价并不相同[14]，见表1。本文将1h的电价等值分成2个时段，一日共48个时段做讨论，并利用后面介绍的多目标最优化方法，做相关的数值模拟与分析。

表1 一天各个时刻充电电费单价

3 系统流程与多目标最优化问题

3.1 系统流程

充电站作为智能电网的重要组成部分，会在各个时段收集进入充电站充电的电动汽车的数量、电池剩余容量及其充电需求等信息。然后，将这些信息上传云端，通过计算机调度中心进行统一的优化处理，得出各个充电桩在不同时段应该给予家用电动汽车充电速率的最优值。最后，计算机调度中心将结果反馈给充电站，充电站按照优化信息安排家用电动汽车进行充电。图3为智能电网模式中充电站的营运流程图。

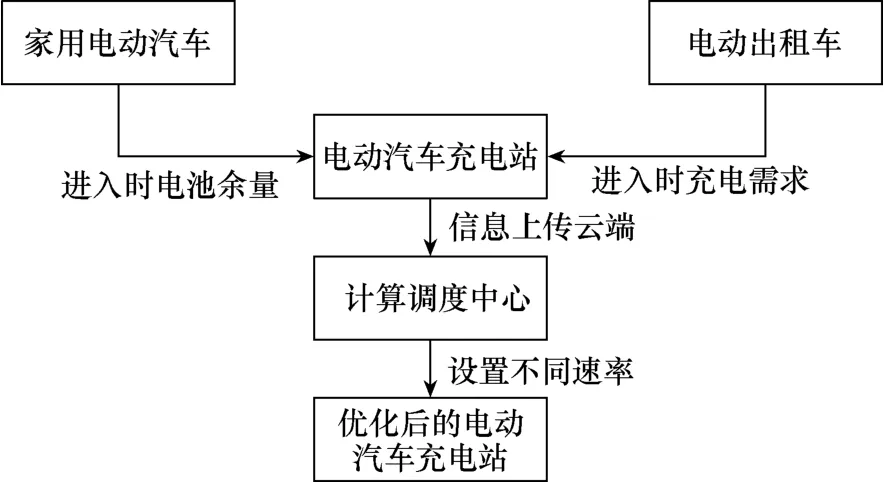
图3 智能电网中的充电站营运流程图

3.2 多目标优化问题

本文中的多目标问题包含最大化一天中充电站的充电服务收益与最大化充电站自身的负载因子。这两个目标将造成权衡问题。当充电站想要获得更高的充电收益时，充电站对各个时段充电速率的规划可能造成充电站一天负载因子的减少；相反地，当想提升充电站一天负载因子时，会造成充电站充电收益的下降。因此，要如何在这个权衡问题的框架下，通过改变各个时段充电站对于家用电动汽车的充电速率来寻找最优解是本次研究的重点。

充电站的充电收益来源于两部分，一部分是家用电动汽车充电所需支付的费用，另一部分是电动出租车充电所需支付的费用。所有家用电动汽车一天的总充电花费EVtotal可表示为

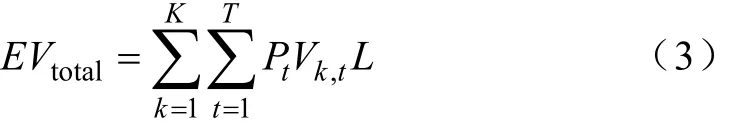
式中，Pt表示一天各个时间段的电价，所有电动出租车一天的总充电花费PETtotal可表示为

式中，Nt表示在 t时刻，在充电站充电的电动出租车数量，Vtaxi表示电动出租车的充电速率，Vtaxi=10kW/h。由式（4）和式（5）可得充电站一天的充电总收益为

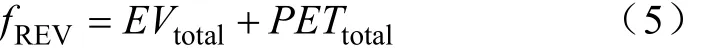
充电站除了要考虑自身收益之外，作为底层电力系统也需注意其自身的负载因子。通常电能的使用者并不在意负载因子，然而负载因子对于发电端的成本或整个电网的稳定度却有非常重要的关系。

负载因子可定义为每时段平均的用电量除以各时段用电量中的最大值[15]。充电站各个时段的负载总量包括给家用电动汽车充电的电量和给电动出租车充电的电量。相关数学符号定义如下。avg表示充电站各个时段的平均用电量，定义为

充电站一天各时段中最大的负载量Emax表示为

较高的负载因子可以保证更良好的电网稳定度并且降低发电的成本。负载因子的定义表示如下[16]：

本文讨论的多目标最优化问题为充电站收益最大化与充电站本身负载因子最大化，就是要同时优化式（5）与式（8）的结果，对应的多目标最优化问题可表示为

3.3 多目标免疫算法

在本文中的多目标最优化问题中，两个目标函数互相冲突，因此无法找到一个解能够同时最优化两个目标。关于多目标最优化问题的解，称之为柏雷多最优解（pareto optimal solution），其特性为：在提升任一目标函数的表现时，必定降低另一个目标函数的表现[17-18]。

在解多目标最优化问题时，多目标免疫算法[19]在解相关问题上拥有突出的收敛性与多样化的优点，使得多目标免疫算法逐渐成为受欢迎的多目标进化算法之一。多目标免疫算法模仿人类的免疫系统并模拟产生抗体（Antibodies）的机制。人类的免疫系统在侦测到病毒后，产生相对应的抗体。除此之外，免疫系统还具有记忆的能力，当遇到相同的攻击时，可自动产生相对应的抗体抵御攻击。此特性可用来加快算法的收敛速度。在多目标最优化的问题中，目标函数可视为抗原（Antigens），而免疫系统所产生的抗体可视为多目标问题的解。抗体与抗原的适合度（Fitness）则可对应到解和目标函数的适合度。所得到的解将存在同一个记忆细胞集合中，透过不断的更新和叠代，可以得到均匀分布的柏雷多最优解。

4 模拟结果与讨论

本文模拟一个充电站在一天的充电情形，通过模拟得到图4，包含30个柏雷多最优解。由于家用电动汽车进入充电站时电池剩余电量是利用随机变量产生，因此每次模拟的结果会略有不同。

在得到柏雷多集合后，为了找出较优的负载因子与充电站可接受的充电收益，必须解决此多准则决策（multiple criteria decision making）问题。多准则决策为帮助决策者在数量有限的方案中，对不同的准则进行分析与筛选，最后选择出符合决策者期望的方案。在多准则决策的方法中，使用曼哈顿最短距离（minimum manhattan distance, MMD）方法来进行决策[20]。曼哈顿最短距离法为选择在柏雷多前沿中与理想矢量具有最短曼哈顿距离的解作为最后的输出结果。

图4 利用多目标免疫算法得到的柏雷多最优解集合

图 5（a）表示充电站用10kW/h的固定充电速率给家用电动汽车充电，得到一天各时段的负载量。通过表 1的计价方式得到充电站一天的总收益为1208美元。图5（b）表示充电站使用多目标最优化方法优化充电速率后，得到一天各时段的负载量。通过表 1的计价方式得到充电站一天的总收益为1249美元。

图5 快速充电站一天各时段的充电负载量

比较充电站在优化前与优化后各时段的负载量得到图 6。发现优化充电站的充电速率后，高峰用电量有明显的减少，离峰时段用电量有所增加，各时段用电量较平均。负载因子从0.413提升到0.476，提升了15.3%。而充电站一天的总收益也从优化前的1208美元，提高到1249美元，收益提升了3.4%。此结果显示本研究提出的多目标最优化方法，能有效地控制智能电网中电动汽车充电速率，进而提升充电站的负载因子与收益。

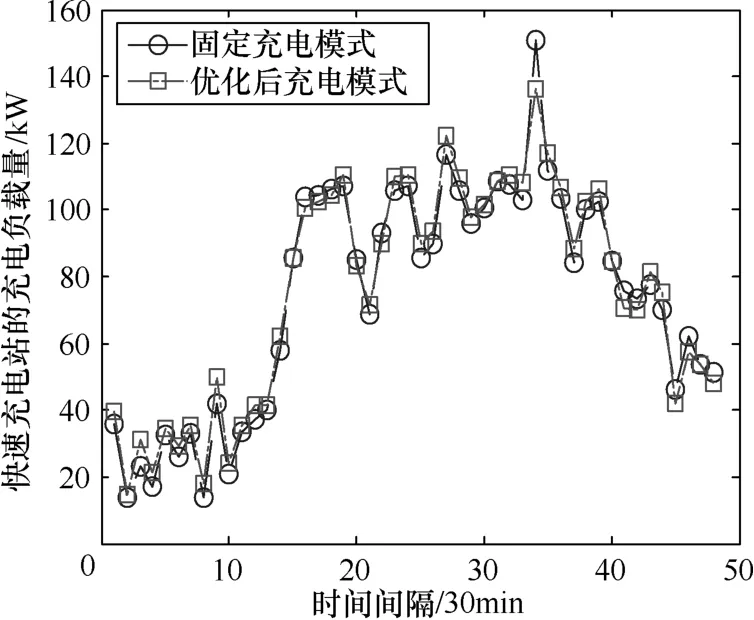
图6 快速充电站在优化前与优化后各时段充电负载量的对比

5 结论

在智能电网的环境下，作为底层电力系统的充电站如果仅考虑如何增加自己供电给用户时的收入，有可能让负载因子处于较低的状态。为了增加电网的稳定度，本文将充电站的服务收入与负载因子作为多目标最优化的目标函数，然后通过多目标免疫算法得到最优解。模拟结果显示充电站在使用这种优化算法后，能同时提升充电站一天的服务收入与负载因子。

[1] 徐武峰. 电动汽车充换电设施投资效益分析[J]. 电气技术, 2015, 16(4)： 108-111.

[2] 吴奇珂, 程帆, 陈昕儒. 5电能替代"战略中电动汽车的推广潜力及经济性分析[J]. 电气技术, 2016, 17(9)：88-92.

[3] 李都红. 智能电网关键技术在新建机场区域型电力网络规划中的集成与应用[J]. 电气技术, 2014, 15(6)：106-108.

[4] 杨冰, 王丽芳, 廖承林, 等. 不确定充电习惯对电动汽车充电负荷需求及充电负荷调节的影响[J]. 电工技术学报, 2015, 30(4)： 226-232.

[5] 潘樟惠, 高赐威. 电动汽车换电网络协调规划[J].电工技术学报, 2015, 30(12)： 480-487.

[6] Z Yang LS, Xing K. Profit maximization for Plug-In electric taxi with uncertain future electricity prices[J].IEEE Trans. Power SystNov, 2014, 29(6)： 3058-3068.

[7] L Catarinucci DD, Tarricone L. An IoT-aware architecture for smart healthcare systems[J]. IEEE Internet of Things J. Dec, 2015, 2(6)： 515-526.

[8] J De Hoog TA, Mareels I. Optimal charging of electric vehicles taking distribution network constraints into account[J]. IEEE Trans. Power Syst Jan, 2015, 30(1)：365-375.

[9] C Chen J W, Kishore S. MPC-based appliance scheduling for residential building energy management controller[J]. Sep, 2013, 4(3)： 1401-1410.

[10] Hsieh J T, Chiu W Y. Implementation of a transparent power information system on campus using existing infrastructures[J]. IEEE Vehicular Technology Conference Workshops, Glasgow, Scotland, May 2015： 1-4.

[11] Chiu W Y. Analysis of an H∞design for dynamic pricing in the smart grid[C]//Proc. IEEE Conference on Decision and Control. NV, USA, 2016： 3234-3239.

[12] Chiu W Y, Sun H, Poor H V. Energy imbalance management using a robust ppricing scheme[J]. IEEE Trans. Smart Grid, 2013, 4(2)： 896-904.

[13] Zhao S, Ming Z. Modeling demand response under time-of-use pricing[Z]. in Proc. 2014： 1948-1955.

[14] http：//www.pjm.com/Search%20Results.aspx?q=miner

[15] M Pedrasa T S, Macgill I. Scheduling of demand side resources using binary particle swarm optimization[J].Aug, 2009, 24(3)： 1173-1181.

[16] K Kumar B S, Wang D. V2G capacity estimation using dynamic EV scheduling[J]. Mar, 2014, 5(2)： 1051-1060.

[17] Chiu W Y. Method of reduction of variables for bilinear matrix inequality problems in system and control designs[J]. IEEE Trans. Syst., Man, Cybern,Syst, 2717, 47(7).

[18] Chiu W Y, Chen B S, Poor H V. A multiobjective approach for source estimation in fuzzy networked systems[J]. IEEE Trans. Circuits Syst. I, Reg. Papers,2013, 60(7)： 1890-1900.

[19] W Y Chiu H S, Poor H V. A multiobjective approach to multimicrogrid system design[J]. Sep, 2015, 6(5)：2263-2272.

[20] Chiu W Y, Yen G G, Juan T K. Minimum manhattan distance approach to multiple criteria deeision making in multiobjective optimization problems[J]. IEE Trans.Evol. Comput., 2016, 20(6)： 972-985.

Multiobjective Optimization based Charging Strategy for Electric Vehicles in Smart Grid

Guan Haoliang1Wang Jinhua1Qiu Weiyu2
(1. School of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350000;2. Department of Electrical Engineering, Yuan Ze University, Taoyuan, Taiwan 32003)

Charging scheduling for electric cars and plug-in electric taxis in the smart grid is considered. A charging station may control the charging rate to maximize its revenue. For the underlying power system, maximizing the corresponding load factor is desired so that the system stability can be ensured. Maximizing the revenue and load factor simultaneously leads to a multiobjective optimization problem. A multiobjective approach is proposed to solve the multiobjective optimization problem,yielding a pareto optimal charging strategy. Numerical analysis is conducted to illustrate the effectiveness of the proposed multiobjective methodology.

smart grid; plug-in electric taxi; multiobjective optimization; pareto optimality

关昊亮（1993-），男，硕士研究生，研究方向为多目标最优化与智能电网。