基于RT-LAB的MPPT控制模拟及试验验证

朱红，马洲俊，张明，嵇文路，卞海红

（1.国网南京供电公司，江苏南京 210019；2.南京工程学院，江苏南京 211167）

如何快速有效地实现最大功率点跟踪（the maximum power point tracking，MPPT），是光伏发电系统中的关键问题。目前，针对MPPT控制器的研究大都采用MATLAB/Simulink搭建模型进行纯数字仿真[1-3]，也有采用硬件搭建模拟光伏发电系统模型进行纯物理模拟[4]，验证控制器算法的优劣。纯数字模拟虽然具备操作简单、参数可变等优点，但是其准确性不及纯物理模拟，且很多实际物理现象无法模拟；纯物理模拟虽然直观、真实、可信，但是其可操作性不强，灵活性不足，无法对实际系统进行充分地模拟研究。

本文结合了物理模拟和数字仿真，对MPPT算法进行硬件模拟，在RT-LAB实时仿真软件[5-7]上对主电路进行数字模拟，结合RT-LAB实时仿真器搭建实时仿真平台，进行数模混合实时仿真研究。在该仿真平台中仿真时间标尺与墙钟时间标尺完全同步，可以模拟各种极端条件下的试验验证。

亦有文献结合RT-LAB半实物仿真技术和光伏MPPT的特点进行过数模混合仿真探索[8-9]，然而未有文献对比不同MPPT算法，研究其适用性和优劣性。本文对比一种改进的MPPT算法与传统MPPT算法，在RT-LAB实时仿真平台中进行数模混合仿真，对比分析改进MPPT算法与传统MPPT算法的控制效果，验证改进控制算法的有效性及优越性。

1 MPPT光伏系统模型

1.1 光伏电池模型

光伏电池的数学模型[10-11]已经普遍应用于太阳能电池的输出特性理论分析中，由厂家提供标准条件（光照强度S=1 000 W/m2，电池温度T=25℃）下光伏电池的测试参数：短路电流Isc、开路电压Uoc、最大功率点电流Im和最大功率点电压Um4个参数。根据以下公式计算当前环境下新的参数

式中：ΔT为参考电池温度与实际电池温度的差值；ΔS为日照强度变化量与参考日照强度的比值；Iscref为外界条件变化时光伏电池的短路电流；Uocref为外界条件变化时光伏电池的开路电压；Imref为外界条件变化时光伏电池的最大功率点电流；Umref为外界条件变化时光伏电池的最大功率点电压；α、β、γ为常数，采用典型值分别等于0.002 5、0.5、0.002 88。根据以下公式得到光伏电池的电流方程：

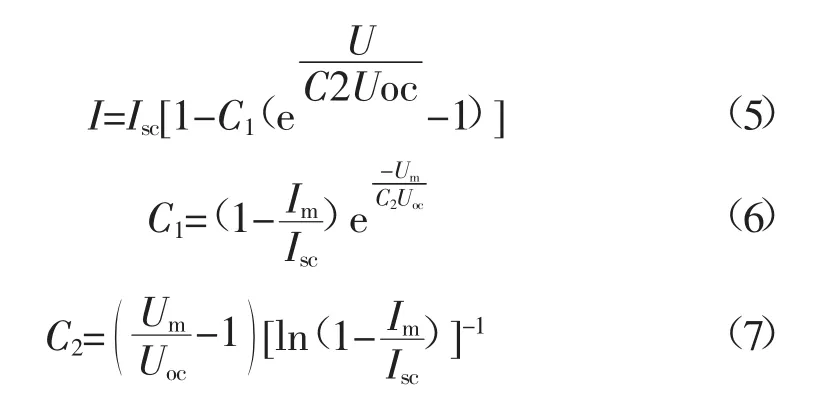
本文采用某公司的光伏电池进行参数模拟，在标准外部环境下（光照强度为1 000 W/m2，电池温度为25℃）电池参数如表1所示。

表1 光伏电池参数Tab.1 PV parameters

1.2 光伏输出特性

光伏电池的性能受光电池PN结参数、光照强度、电池温度等多种因素影响，因此光伏电池输出特性是非线性变化的。在多种因素中，太阳光照强度和电池温度的影响更为直接、明显。为了更好地利用光伏电池，需要对不同外界条件下的光伏电池输出特性进行了解和分析。如图1所示为不同光照强度下的P-U曲线。

图1 不同光照强度下的P-U曲线Fig.1 P-U curves under different light intensities

由图1可知，随着光照强度按照400 W/m2、600 W/m2、800 W/m2、1 000 W/m2变化时，最大功率点输出功率不断增大，而最大功率点处电压不明显，根据功率与电压电流的关系可知，最大功率点处电流值不断增大，即最大功率点处功率和电流随着光照强度增大有显著增加，光照强度对最大功率点处电压影响较小。如图2所示为不同电池温度条件下的P-U曲线。

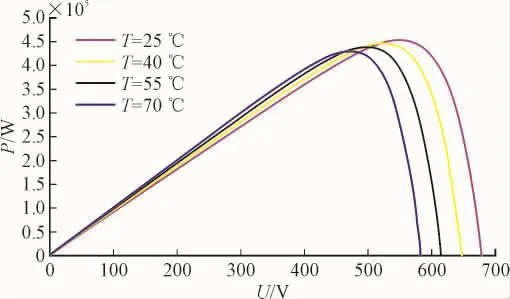
图2 不同电池温度下的P-U曲线Fig.2 P-U curves under different battery temperatures

由图2可知，随着温度按照25℃、40℃、55℃、70℃变化时，在最大功率点之前，相同电压情况下，功率略有升高；到达最大功率点处时，输出功率和电压值都略有降低，即随着温度升高，最大功率点输出功率降低，同时最大功率点处电压也略有降低。

2 MPPT算法

本文采用一种改进的扰动观察法：基于|（dP/dV）/P|的扰动观察法[12]进行半实物仿真验证，并与常见的MPPT算法进行对比分析。本文与之进行对比的常见MPPT算法包括扰动观察法[13-15]（P&O）和电导增量法[16-18]（INC）。

扰动观察法是实现MPPT最常见的自寻优类方法之一。其基本思想是：首先扰动光伏电池的输出电压（或电流）；其次观测光伏电池输出功率的变化，根据功率变化的趋势连续改变扰动电压（或电流）方向，使光伏电池最终工作于最大功率点。其控制流程图如图3所示。

图3 定步长扰动观察法算法流程图Fig.3 Flow chart of constant step perturbation observation method

当负载特性与光伏电池特性的交点在最大功率点左侧时，MPPT控制会使交点处的电压升高；而当交点在最大功率点右侧时，MPPT控制会使交点处的电压下降。如果持续这样的搜索过程，最终可使系统跟踪光伏电池的最大功率点运行。即使用ΔP/ΔU代替dP/dU，期望得出的工作点满足ΔP/ΔU=0，即为最大功率点。

定步长的扰动观察法存在振荡和误判问题[19]，使系统不能准确地跟踪到最大功率点，造成了能量损失，因此需要对定步长的扰动观察法进行改进。

电导增量法从光伏电池输出功率随输出电压变化率而变化的规律出发，推导出系统工作点位于最大功率点时的电导和电导变化率之间的关系，进而提出相应的MPPT算法。实际中以ΔI/ΔU近似代替dI/dU，则使用电导增量法进行最大功率点跟踪时判据为：

定步长电导增量法算法流程图如图4所示。电导增量法算法计算量大、较为复杂，对控制系统要求较高，也对硬件尤其是传感器的精度和速度要求较高，同时增加硬件成本[20]。考虑到定步长扰动观察法和定步长电导增量法的控制缺陷，本文采用一种改进的变步长扰动观察法：基于|（dP/dV）/P|的扰动观察法进行半实物仿真验证，既能避免定步长扰动观察法的振荡和误判问题，又能避免对控制器的高要求，降低控制器硬件成本。该算法在传统定步长扰动观察法基础上增加了步长判断模块，以|（dP/dV）/P|作为判断因子，外界条件变化时，|（dP/dV）/P|曲线变化不大，所以该算法可以适应多变的外界条件，保证系统的稳定运行。本文采用2级式光伏并网系统，DC-DC升压模块采用Boost升压电路，实际控制量为Boost电路开关管驱动信号的导通比，通过IGBT信号控制Boost电路，实现最大功率点跟踪，其控制流程图如图5所示。

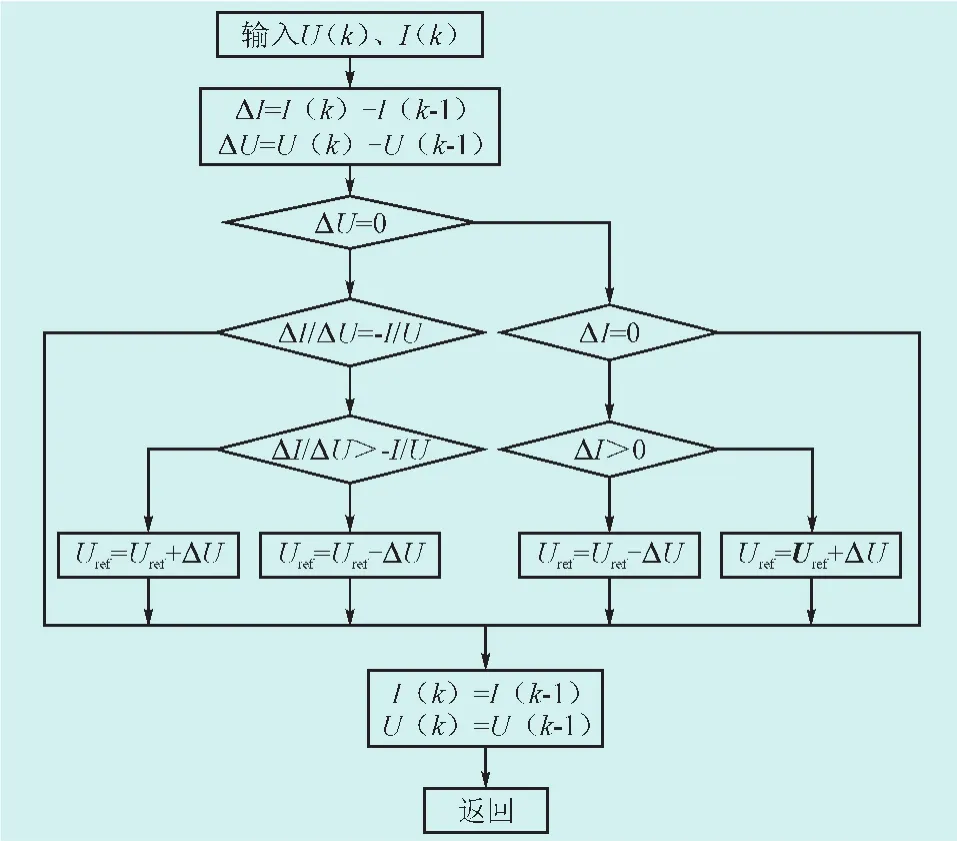
图4 定步长电导增量法算法流程图Fig.4 Flow chart of constant step conductance increment method

图5 基于|（dP/dV）/P|的扰动观察法算法流程图Fig.5 Algorithm flow chart of disturbance observation method based on|（dP/dV）/P|

光伏电池具有明显的非线性特性，光伏电池工作电压U距离最大功率点电压Um较远时跟踪速度缓慢，当U在Um左侧时更为显著。所以在Um的左侧，设定U＜0.7 Um时，系统采用较大跟踪步长，U＞0.95 Um时，系统采用较小跟踪步长。根据本文中光伏电池的数学模型绘制如图6所示的|（dP/dV）/P|曲线，计算步长判定边界值。

图6 |（dP/dV）/P|曲线图Fig.6 |（dP/dV）/P|graph

由图6可知，0.7 Um对应|（dP/dV）/P|值为0.003，即|（dP/dV）/P|＞0.003时采用较大步长，设定较大步长ΔDmax=0.003；0.95Um对应|（dP/dV）/P|值为0.001，即|（dP/dV）/P|＜0.001时采用较小步长，设定较小步长ΔDmin=0.000 1；当0.001＜|（dP/dV）/P|＜0.003采用中等步长，设定中等步长为ΔDmid=0.001。

3 半实物实时仿真试验验证

3.1 实时仿真平台构建

RT-LAB半实物仿真平台基于Matlab/Simulink模型，它很好地实现了基于模型的系统设计和测试，方便将电力电子以及电力系统控制算法与被控系统的仿真模型进行完全交互，系统具有开放性和灵活性的特点。RT-LAB半实物仿真平台具体结构示意图如图7所示。

平台包括OP5600仿真目标机、上位机、实物控制器、示波器和信号发生器。目标机配置为：4U机箱，Intel i7 6核3.3 GHz，2个CPU，4G内存，5142 FPGA板，I/O载板。平台包括Redhat Linux实时操作系统和I/O卡驱动；上位机配置为：Core（TM）i5-3230 M CPU2.60 GHz，4G内存，Win7 64位操作系统；实物控制器为某公司的MC56F8257芯片，软件开发环境选择Code Warrior for Microcontrollers10.5，采用C语言编写程序，利用实时调试工具FreeMASTER1.4和示波器完成软件调试；上位机与目标机之间通过TCP/IP连接；目标机与实物控制器之间采用OP5142 FPGA卡及杜邦线进行数据传输；信号发生器和示波器为实时仿真的进行提供数据观测和验证帮助。

采用3种MPPT算法进行MPPT硬件控制器设计，RT-LAB模拟量输出（控制器输入）分别为光伏电压Vpv和光伏电流Ipv，数字量输入（控制器输出）为Boost电路IGBT信号，所采用的光伏并网控制电路结构图如图8所示。

图7 RT-LAB半实物仿真平台结构示意图Fig.7 Schematic diagram of RT-LAB hardware in the loop simulation platform

图8 光伏并网控制电路结构图Fig.8 Structure diagram of photovoltaic grid connected control circuit

考虑到硬件控制器模拟量输入范围为：0～3.3 V，光伏电压Vpv和光伏电流Ipv分别缩小到1/300输入硬件控制器，RT-LAB仿真步长为1×10-5s，MPPT控制器采样周期为1×10-4s，控制器送回RT-LAB的IGBT信号为5 V，10 kHz方波信号，驱动Boost电路，实现最大功率点跟踪。

本文中MPPT控制器需要检测的信号为光伏电池输出的直流电压、直流电流。采用MC56F8257内部集成的ADC模块即可实现AD。硬件控制器需输出1路PWM信号作为Boost升压电路的功率开关的控制信号。由于MC56F8257内部集成了功能强大、性能优越的eFlexPWM模块，完全能满足本控制器的需求。其硬件资源配置如表2所示。

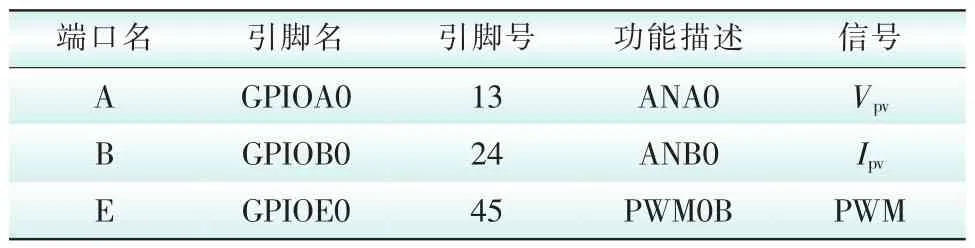
表2 MPPT控制器硬件资源配置表Tab.2 Hardware resource configuration table for MPPT controller

3.2 RT-LAB实时仿真模型

搭建基于RT-LAB的实时仿真模型，根据3种MPPT算法进行半实物实时仿真，并结合RT-LAB的在线调参、实时调参等功能进行参数优化，实时仿真模型包括SM主电路模块、SC监测子模型，模型如图9—图11所示，为实时仿真主模型，采用10 μs仿真步长进行试验验证，包括SM主电路子模型及SC监测子模型，其中SM主电路模型主要负责光伏并网系统的计算，外界环境、电网故障等状况的模拟，模拟信号数字信号交互等；而SC监测子模型则向SM主电路模型输出控制信号，包括光照强度改变、电池温度改变、系统故障灯控制信号，同时采集系统观测量并在示波器中显示，实现对并网系统的实时监测。

图9 RT-LAB实时仿真模型主模型Fig.9 MMaster model of RT-LAB real time simulation model

图10 RT-LAB实时仿真模型SM主电路模块Fig.10 10 RT-LAB real-time simulation model SM main circuit module

采用3块不同的MPPT硬件控制器分别连接RTLAB进行对比分析。电池温度不变（25℃）、光照强度变化为0～0.5s时光照强度为1000W/m2，0.5 s时光照强度降为200 W/m2，0.75 s光照强度升高至1 000 W/m2，基于3种MPPT算法的半实物仿真验证结果如图12—图14所示。

由图12—图14可知，光照强度S=1 000 W/m2时，3种MPPT算法的实验仿真结果显示光伏输出电压为550 V、光伏输出电流为820 A；光照强度S=200 W/m2时光伏输出电压为497 V，光伏输出电流为155 A，与理论仿真结果相符。同时，当光照强度改变时，系统能够快速跟踪至新的最大功率点，验证了硬件控制器控制功能的有效性和快速性。

3种MPPT算法中，传统扰动观察法和电导增量法在最大功率点处都有较大振荡，而基于|（dP/dV）/P|的变步长扰动观察法振荡范围小于2种传统MPPT算法，体现了算法良好的稳定性，同时该算法在光照强度改变时，跟踪至新的最大功率点所需时间也小于2种传统MPPT算法，体现了基于|（dP/dV）/P|的变步长扰动观察法对环境的适应能力较强，有良好的运行稳定性。

图11 RT-LAB实时仿真模型SC监测子模块Fig.11 RT-LAB real time simulation model SC monitoring sub module

图12 扰动观察法光伏输出电压电流Fig.12 Photovoltaic output voltage and current by perturbation observation method

图13 电导增量法光伏输出电压电流Fig.13 Photovoltaic output voltage and current by conductance increment method

当光照强度不变（1 000 W/m2），电池温度变化时，其变化过为：0～0.5 s时电池温度为50℃；0.5 s时降为15℃；0.75s时电池温度升高至50℃。基于3种MPPT算法的半实物仿真验证结果如下图15—图17所示。

由图15—图17可知，光照强度固定1 000 W/m2，温度50℃时，3种MPPT算法的实验仿真结果显示光伏输出电压约为510 V、光伏输出电流为860 A；温度15℃时，光伏输出电压为560 V，光伏输出电流为810 A，与理论仿真结果基本相符。同时，当电池温度改变时，系统能够快速跟踪至新的最大功率点，验证了硬件控制器控制功能的有效性和快速性。

3种MPPT算法中，传统扰动观察法和电导增量法在最大功率点处都有较大振荡，而基于|（dP/dV）/P|的变步长扰动观察法振荡范围小于2种传统MPPT算法，体现了算法良好的稳定性。同时，该算法在电池温度改变时，跟踪至新的最大功率点所需时间也小于2种传统MPPT算法，体现了基于|（dP/dV）/P|的变步长扰动观察法对环境的适应能力较强，有良好的运行稳定性。

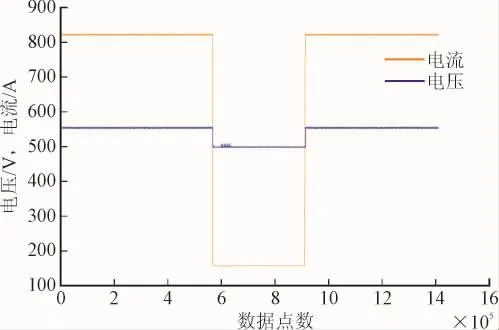
图14 基于|（dP/dV）/P|的扰动观察法输出电压电流Fig.14 Output voltage and current of disturbance observation method based on|（dP/dV）/P|

图15 扰动观察法光伏输出电压电流Fig.15 Photovoltaic output voltage and current by perturbation observation method

图16 电导增量法光伏输出电压电流Fig.16 Photovoltaic output voltage and current by conductance increment method

4 结语

本文从MPPT控制实物化角度研究不同MPPT算法，并采用1种改进的MPPT算法进行硬件控制器设计，结合RT-LAB实时仿真平台建立数字主电路，进行数模混合实时仿真验证，对比分析改进MPPT算法与传统MPPT算法的控制效果。实验结果表明：3种MPPT算法中，传统扰动观察法和电导增量法在最大功率点处都有较大振荡，而基于|（dP/dV）/P|的变步长扰动观察法振荡范围小于2种传统MPPT算法，体现了算法良好的稳定性。同时，该算法在光照强度及电池温度改变时，跟踪至新的最大功率点所需时间也小于2种传统MPPT算法，体现了基于|（dP/dV）/P|的变步长扰动观察法对环境的适应能力较强，有良好的运行稳定性。

图17 基于|（dP/dV）/P|的扰动观察法输出电压电流Fig.17 Output voltage and current of disturbance observation method based on|（dP/dV）/P|

[1]张峥，南海鹏，余向阳，等.基于Matlab/Simulink的两级式光伏并网系统仿真分析[J].可再生能源，2010，28（1）：81-84.ZHANG Zheng，NAN Haipeng，YU Xiangyang，et al.Two-stage grid-connected photovoltaic system simulation based on matlab/simulink[J].Renewable Energy Resources，2010，28（1）：81-84（in Chinese）.

[2]ORABI M，HILMY F，SHAWKY A，et al.On-chip integrated power management MPPT controller utilizing celllevel architecture for PV solar system[J].Solar Energy，2015（117）：10-28.

[3]董丽娜，肖志刚，高立艾，等.基于SIMULINK仿真的太阳能光伏系统最大功率点跟踪[J].中国农机化学报，2016，37（2）：227-232.DONG Lina，XIAO Zhigang，GAO Liai，et al.Solar photovoltaic maximum power point tracking system based on SIMULINK simulation[J].Journal of Chinese Agricultural Mechanization，2016，37（2）：227-232（in Chinese）.

[4]王敏，崔连延，孙静静.太阳能电池工程用数学模型的建立[J].科学技术与工程，2010，10（35）：8812-8815.WANG Min， CUI Lianyan， SUN Jingjing.Solar cell engineering by establishing mathematics model[J].Science Technology&Engineering，2010，10（35）：8812-8815（in Chinese）.

[5]孙航，杜海江，季迎旭，等.光伏分布式MPPT机理分析与仿真研究[J].电力系统保护与控制，2015，43（2）：48-54.SUN Hang，DU Haibing，JI Yingxu，et al.Photovoltaic distributed MPPT mechanism analysis and simulation study[J].Power System Protection&Control，2015，43（2）：48-54（in Chinese）.

[6]刘立立，林永君，刘卫亮.基于改进MPPT的光伏发电系统仿真研究[J].电力科学与工程，2016，32（11）：23-28.LIU Lili，LIN Yongjun，LIU Weiliang.Simulation research of photovoltaic power generation system based on improved MPPT[J].Electric Power Science&Engineering，2016，32（11）：23-28（in Chinese）.

[7]郑鹤玲，葛宝明，毕大强.基于RT-LAB的光伏发电系统实时仿真[J].电工电能新技术，2010，29（4）：62-66.ZHENG Heling，GE Baoming，BI Daqiang.RT-LAB based real-time simulation of photovoltaic power generation system[J].Advanced Technology of Electrical Engineering&Energy，2010，29（4）：62-66（in Chinese）.

[8]周林，贾芳成，郭珂，等.采用RT-LAB的光伏发电仿真系统试验分析[J].高电压技术，2010，36（11）：2814-2820.ZHOU Lin，JIA Fangcheng，GUO Ke，et al.Testing analysis on a kind of PV generation simulation system using RT-LAB[J].High Voltage Engineering，2010，36（11）：2814-2820（in Chinese）.

[9]薛云灿，李彬，王思睿，等.基于功率二次微分的光伏系统改进MPPT算法研究[J].电网与清洁能源，2015，31（6）：117-123.XUE Yuncan，LI Bin，WANG Sirui，et al.An improved MPPT algorithm based on power quadratic differential for photovoltaic system[J].Power System&Clean Energy，2015，31（6）：117-123（in Chinese）.

[10]傅望，周林，郭珂，等.光伏电池工程用数学模型研究[J].电工技术学报，2011，26（10）：211-216.FU Wang，ZHOU Lin，GUO Ke.Research on engineering analytical model of solar cells[J].Transactions of China Electrotechnical Society，2011，26（10）：211-216（in Chinese）.

[11]孟彦京，徐晓龙.光伏电池数学模型的LabVIEW仿真分析[J].电测与仪表，2015，52（2）：38-42.MENG Yanjing，XU Xiaodong.Simulation and analysis and of the photovoltaic cell mathematical model based on LabVIEW[J].Electrical Measurement&Instrumentation，2015，52（2）：38-42（in Chinese）.

[12]李连玉.太阳能光伏发电逆变控制器研究[D].北京：北京化工大学，2012.

[13]AHMED J，SALAM Z.An improved perturb and observe（P&O）maximum power point tracking（MPPT）algorithm for higher efficiency[J].Applied Energy，2015（150）：97-108.

[14]熊远生，俞立，徐建明.固定电压法结合扰动观察法在光伏发电最大功率点跟踪控制中应用[J].电力自动化设备，2009，29（6）：85-88.XIONG Yuansheng，YU Li，XU Jianming.MPPT control of photovoltaic generation system combining constant voltage method with perturb-observe method[J].Electric Power Automation Equipment，2009，29（6）：85-88（in Chinese）.

[15]朱铭炼，李臣松，陈新，等.一种应用于光伏系统MPPT的变步长扰动观察法[J].电力电子技术，2010.44（1）：20-22.ZHU Minglian， LI Chensong， CHEN Xin， et al.A variable step size P&O MPPT method for PV systems[J].Power Electronics，2010.44（1）：20-22（in Chinese）.

[16]XU Z，YANG P，ZHOU D，et al.An improved variable step size MPPT algorithm based on INC[J].Journal of Power Electronics，2015，15（2）：487-496.

[17]汤济泽，王丛岭，房学法.一种基于电导增量法的MPPT实现策略[J].电力电子技术，2011，45（4）：73-75.TANG Jize，WANG Congling，FANG Xuefa.MPPT implementation strategy based on the conductance increment method[J].Power Electronics，2011，45（4）：73-75（in Chinese）.

[18]黄舒予，牟龙华，石林.自适应变步长MPPT算法[J].电力系统及其自动化学报，2011，23（5）：26-30.HUANG Shuyu， MOU Longhua， SHILin.Adaptive variable step size MPPT algorithm[J].Proceedings of the Chinese Society of Universities for Electric Power System&Its Automation，2011，23（5）：26-30（in Chinese）.

[19]王春圣.扰动观察法的MPPT负载突变误判现象研究[J].华东交通大学学报，2012，29（3）：83-87.WANG Chunsheng.On misjudgment phenomenon of MPPT load mutation based on perturbation and observation method[J].Journal of East China Jiaotong University，2012，29（3）：83-87（in Chinese）.

[20]栗晓政，孙建平.基于分段数值逼近的自适应步长电导增量法MPPT控制仿真[J].太阳能学报，2012，33（7）：1164-1170.LI Xiaozhen，SUN Jianping.Simulation of auto-adapted step size incremental conductance method MPPT control based on segmented numerical approximation[J].Acta Energiae Solaris Sinica，2012，33（7）：1164-1170（in Chinese）.