含参不等式恒成立问题的思维途径
于 晴
(河北省唐山市第二中学 063000)
含参不等式恒成立问题的思维途径
于 晴
(河北省唐山市第二中学 063000)
含参不等式问题是高考中常见题型.本文就这类问题的求解方法加以分类,并举例说明.这对提高解答该类问题的能力,有参考价值.
含参不等式;恒成立;问题转化
含有参数字母的不等式恒成立问题综合性强,融合了函数、方程、不等式、三角、数列等各知识点,涉及到诸多数学思想方法,既是高中数学中的典型问题,也是高考的热点题型.本文就求解这类问题的若干思维途径总结如下.
一、选择恰当的主元
从不同的角度分析不等式的结构特征,选择恰当的主元,构造出相应的函数,利用这个函数的有关性质来解决问题.

分析本题常规思路是把左式中的log3x视为一个字母的变元,则可化为二次式问题,但系数中的log2m在变动,不易把握.若视log2m为一个字母的变元,则可化为关于这个字母的一次式问题,容易掌握.

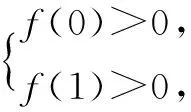
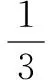
点评本题求解的关键是改变常规思维,变更主元,从而化二次式为一次式,使问题化难为易.选准观察角度,寻找到恰当的着手点,是简捷顺畅解题的关键所在.一般情况下,已知取值范围的字母(如本例中的log2m)为主元,常使问题变得简单易解.
二、分离参数
在含参数的不等式中,如果能将参数解出来,那么可转化为求函数的最值问题.
例2 已知不等式x2+(m+1)x+1≥0在x∈[0,+∞)时恒成立,求实数m的取值范围.


综上得m的取值范围是[-3,+∞).
三、变量代换
数学解题中,如果能作出恰当的代换,那么可将复杂的式子简单化,隐蔽的关系明朗化,从而为解题开辟通道.如上述的例1.现再看一例.
例4 对于满足16x2+9y2-32x+18y-119=0的实数x,y,如果不等式x+y-k>0恒成立,求k的取值范围.


而5sin(θ+φ)的最小值是-5,从而得k的取值范围是(-∞,-5).
四、利用切线
将不等式转化为一条曲线与一条动直线的高低位置关系问题.利用动直线与曲线的邻界位置——相切来解决问题.






[1]戚有建.如何选定主元[J].数学通讯,2014(7、8):5~7.
[2]郑一平.常规的分离参数解法为何半途而废[J].数学通讯,2014(4):12~13.
[3]吴佐慧,林军,刘合国.高考全国卷含参不等式恒成立问题的探究[J].中学数学,2014(2):85~87.
[4]滕中华,章才良.例析“分离参数法”在含参不等式中的应用[J].福建中学数学,2014(4):42~44.
[5]刘鹏.参数取值范围问题的求解方法[J].高中数学教与学,2014(1):19~21.
G632
A
1008-0333(2017)31-0041-02
2017-07-01
于晴,河北省唐山市第二中学 ,在校学生.
杨惠民]

