浅谈高中数学教材中“算两次”的思想
俞昉昉
(江苏省海门市第一中学 226100)
浅谈高中数学教材中“算两次”的思想
俞昉昉
(江苏省海门市第一中学 226100)
本文从教材中撷取一些素材,漫谈高中数学教材中算两次的思想.
算两次;数学方法
“将一个量用两种方法分别算一次,由结果相同得到等式”,这是一种非常有用的思想方法,叫做“算两次”(G.Fubini原理).苏教版教材选修2-3《计数原理》章节复习中提到了这种思想.“算两次”思想的应用常见于数学竞赛,但事实上这种思想方法在高中数学教材中并不鲜见,一些重要的定理和公式的证明中就渗透着“算两次”的数学思想方法.算两次的运用相当广泛,散见于各层级、各类型数学问题中,如组合论证、几何问题、函数与方程、计数应用等.
一、算两次与数学定理、公式的推导
寻找等量关系列方程的实质就是抓住一个量,挖掘已知条件,从两种角度表示同一个量,进行两次演算,即一个量,算两次.许多数学公式的推导和证明都可以采用算两次的思想.


苏教版教材上采用算两次的方法推导数学定理、公式的地方还有很多.如等差数列前n项和公式的推导所运用的倒序相加法,推导点到直线的距离公式所采用的等面积法,立体几何中求点面距所用的换顶点的方法,复合函数求导公式的引入,解析几何中推导圆锥曲线标准方程时所立的等量关系式等等都是算两次的典型范例.
二、算两次与组合恒等式
组合恒等式的证明,如果仅仅采用组合数的定义和阶乘运算,有时计算繁杂,不得其法.在证明某些组合恒等式时还可以考虑采用比较系数法和组合分析法.比较系数法指的是利用二项式定理展开式的两边对应的同次幂的系数相等获得等式.组合分析法就是通过构造具体的组合计数模型,再根据组合数的加法原理和乘法原理得到恒等式两边相等.这两种方案都是采用算两次的方法.
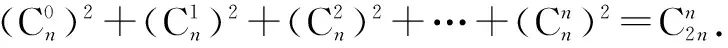
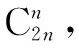
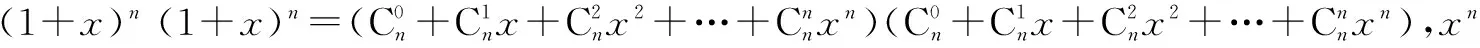
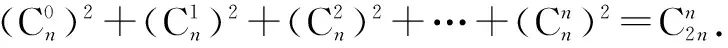

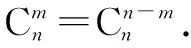

三、算两次与几何问题
研究一些几何问题,我们也常常采用算两次的方法,着眼于从两个方面计算同一线段的长度、同一图形的面积、同一几何体的体积.
例3 (苏教版必修2教材P55)如果用半径为r的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是多少?

例4 (苏教版选修2-2教材P66)(1)已知正三角形的边长为a,求它的内切圆的半径r;(2)已知正四面体的棱长为a,求它的内切球的半径r.
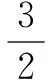
除了上述三个几何类问题,教材中还有不少定义、公式和元素也有多种表达形式,如:平面向量的数量积,圆锥曲线的定义,直线的斜率,不同数列的公共项问题等等,正是基于它们的多面性,算两次方法才得以实施.
算两次作为一种常用的数学方法,如果题目中的某些对象(几何对象或代数对象)具有“双重身份”或“两面性”,则可优先考虑对其“演算两次”.算两次作为一种重要的数学思想,其实质是将同一个量用不同的方法计算两次,通过“殊途同归”达到“出奇制胜”的目的.在教学中,教师应该发挥教材的母体性,深度挖掘教材中的素材,整合知识,提炼思想方法,提升学生的思维品质.
[1]徐达育,钱军先. 摭谈“算两次”方法在高中数学教学中的挖掘与提炼[J]. 福建中学数学,2015(11).
[2]付秀凤. 高中数学解题中“算两次”思想方法的应用探析[J]. 数学学习与研究,2015(13).
G632
A
1008-0333(2017)31-0022-02
2017-07-01
俞昉昉(1985.04-),女,江苏省南通人,本科,中级职称,从事高中数学教学与研究.
杨惠民]

