运用赤足迹多元回归分析同质人群身高

乔胜男，朱玉婷

（中国刑事警察学院，辽宁 沈阳 110035）

运用赤足迹多元回归分析同质人群身高

乔胜男，朱玉婷

（中国刑事警察学院，辽宁 沈阳 110035）

通过选取相同地区、不同年龄、不同性别的120份赤足迹样本，分别对跟压后缘凸点到五趾前缘凸点的距离、跟压后缘凸点到前掌内外侧凸点的距离进行测量，使用SPSS统计分析软件对数据进行多元回归分析和逐步回归分析，发现七个距离与身高之间存在线性相关关系，建立相应的数学模型并得出回归方程，比较模型之间的误判率和准确度，为利用足迹分析同质人群身高提供更可靠有力的方法。

赤足迹；同质人群；身高分析；多元回归

传统分析身高的方法基于足长[1]这一单一元素分析，该方法简单但是也存在自身的局限性，不能涵盖不同种族、不同地域、不同生活环境等客观差异对身高的影响。本文通过对同一地区人群的足迹进行采集并扫描入库，使用数码分规测量统计跟压后缘凸点到五趾前缘凸点的距离、跟压后缘凸点到前掌内外侧凸点的距离七个长度，分析同一地区这七个距离与身高之间的相关性，得出相应的回归方程，为根据足迹推算身高提供新方法。

一、实验部分

（一）实验数据的收集

通过测量来自同一省份、不同性别、不同年龄的健康人群140名，且足部健康无任何疾病。借助油墨捺印盒，遵循罗宾斯采集足迹步骤[2]对实验者左右足都进行采集。并将这些样本扫描入库，剔除采集质量较差的足迹样本，最终选取较好的足迹样本共计120份。在身高测量时实验者光脚靠墙站立且手悬空下垂，是头部定点（在法兰克福水平面[3]）与地板的垂直距离，用标准计量方式标记测量。

（二）实验数据的选取

为了使得测量的数据更加准确，基于易于发现便于测量的原则，对捺印的足迹样本选择了跟压后缘凸点到五趾前缘凸点的距离、前掌宽、后跟宽、跟压后缘凸点到前掌内外侧凸点的距离。考虑到现场出现的足迹，不论清晰的或模糊的，跟压后缘和五趾压前缘出现率比较高，提出后跟的宽度较难测定，本实验最终选取的足迹特征点是五趾前缘凸点分别为A、B、C、D、E；跟压后缘凸点为O点，前掌内外侧凸点为M、N点；（见图1），分析足长测量使用的数据分别是：

1.跟压后缘凸点到拇趾前缘凸点的距离为LOA；

2.跟压后缘凸点到第二趾前缘凸点的距离为LOB;

3.跟压后缘凸点到第三趾前缘凸点的距离为LOC;

图1 足迹测量图

4.跟压后缘凸点到第四趾前缘凸点的距离为LOD;

5.跟压后缘凸点到第五趾前缘凸点的距离为LOE

6.跟压后缘凸点到前掌内外侧凸点的距离为LOM;

7.跟压后缘凸点到前掌内外侧凸点的距离为LON；

使用数码分规将以上七个长度一一进行测量并记录下来，由数据可以看出足长与身高之间的大致关系。

二、统计分析

（一）数据录入EXCEL表格并进行预处理

使用EXCEL表格对数据进行预处理分析并画出散点图，（见图2-1、图2-2），目的是为了查看输入错误，对分析结果造成影响，及时对数据进行分析与修正，快速排除特异点。

从散点图可以看出左右脚的七个距离长度与身高具有很高的相关性，并且这七个变量与身高之间可能存在线性相关，使用SPSS软件对数据进行进一步的分析验证。

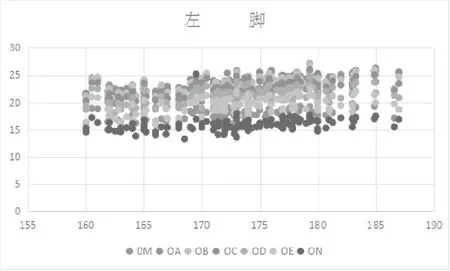
图2-1 左脚各测量值与身高之间的散点图

（二）利用SPSS数理统计软件对数据进行显著性检验分析

在使用SPSS软件对数据进行分析时，为了便于观察将使用x1表示OA，x2表示OB，x3表示OC，x4表示OD，x5表示OE，x6表示OM，X7表示ON。

表1 多个测量值与身高之间的相关性分析

从表格1中可以看出x1与x2、x3、x4、x5、x6、x7的相关性系数分别为0.930、0.904、0.824、0.743、0.142、0.585；x2 与 x3、x4、x5、x6、x7的相关性系数分别为0.974、0.924、0.871、-0.103、0.568；；x3 与 x4、x5、x6、x7的相关性系数分别为0.964、0.905、-0.190、0.557；x4与x5、x6、x7的相关性系数分别为0.949、-0.358、0.511；x5与x6、x7的相关性系数分别为-0.487、0.445；x6与x7的相关性系数为0.111；Pearson相关系数反映相关性的强弱，该表格反映的数据可以说明足长与X1、x2、x3、x4、x5、x7是具有较高的相关性，与x6的相关性较弱。在以下的试验中需要去除前掌内缘凸点到跟后缘凸点的距离这一变量，其他的变量之间具有较高相关性。

（三）多元回归模型分析

在相关性较高的变量和身高之间，使用多元回归模型分析身高。在建立模型的时候，应该对变量进行筛选，这就需要根据某个变量t值大小来确定，将不显著的变量剔除。本实验过程中使用多元逐步回归分析的方法对变量进行选择，见表2。

表2 左脚模型汇总

在模型1中，进入模型的自变量是X1，多元相关系数为0.639；在模型2中，进入模型的自变量是x1和x7，在系数上标注a和b代表的是进入模型相关系数对应的自变量，调整的系数R2数据较大代表模型效果比较好，在模型1和模型2之间的比较后发现模型1的效果较好于模型，标准估计的误差约为5.03。

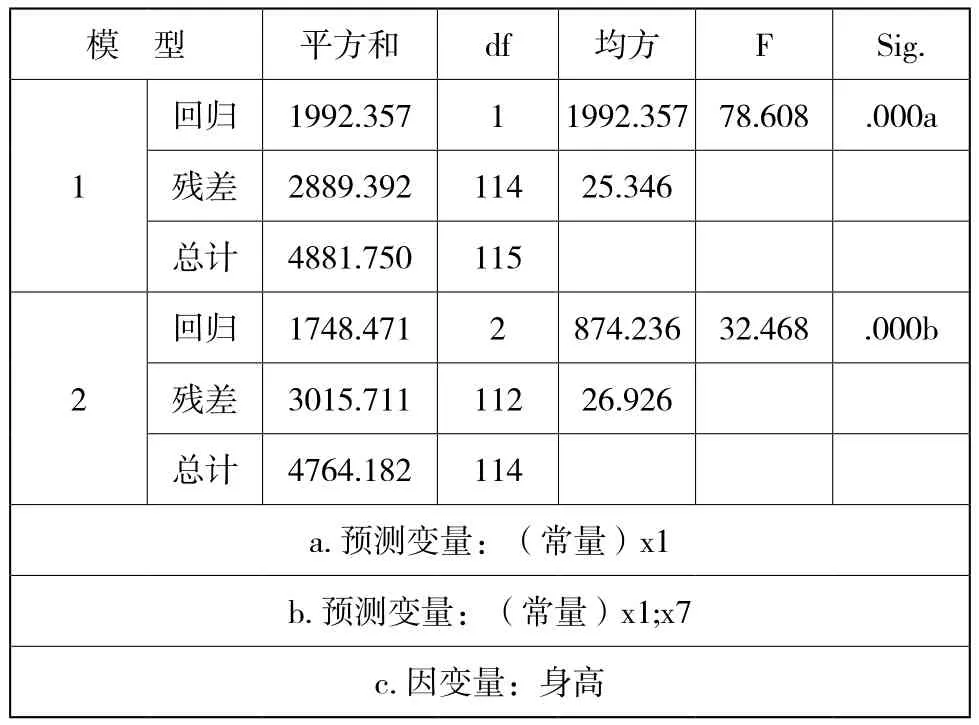
表3 两个回归模型的整体显著性检验

表格3为两个回归模型的整体显著性检验。由表3可知两个模型的标准差均为0.000＜0.01，两个模型的F值分别为78.608和32.468，模型整体显著性检验F值均已达到显著性水平，每个模型模型中的变量解释能力均达到显著性水平，即两个模型的变量系数不为零，两个模型中各个变量来解释身高是有意义的。

表4 模型参数及检验结果

表格4给出了身高与变量之间关系的系数，结合模型检验结果可以得出最佳的模型应该是模型1，即身高S=100.627+3.06*x1，转化到测量的变量上就是身高S=100.627+3.06*（足跟后缘凸点到拇趾前缘凸点的距离）。在逐步回归分析过程中，剔除了其他六个对模型的贡献率不高的变量。

（四）线性回归模型分析

使用SPSS统计分析软件中的回归分析功能，建立各变量与足长之间的系数方程并进行系数评价与比较，见表格5。从表格5可以看出，最佳的线性回归模型就是S=101.578+3.019*x1，相比较其他公式，该公式的标准误差最小。

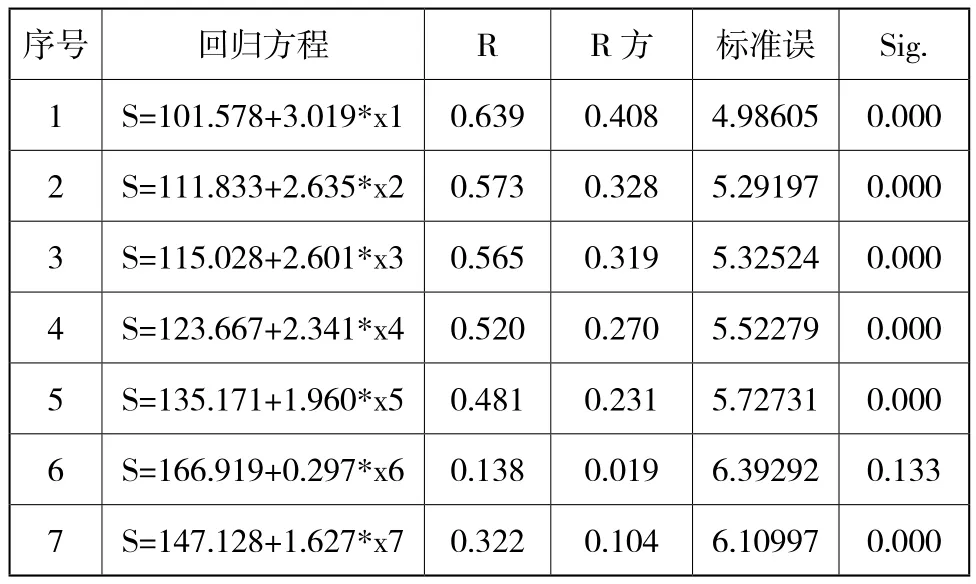
表5 线性回归模型建立表

三、结果统计评价

将上述的实验结果进行验证，左脚的变量所得的模型均与X1有关，根据回归

分析中的逐步回归模型建立的方程式是身高S=100.627+3.06*（足跟后缘凸点到拇趾前缘凸点的距离），标准误差较低；而使用线性回归分析模型建立的方程式是身高S=101.578+3.019*（足跟后缘凸点到拇趾前缘凸点的距离），二者使用的原理不同，得出的实验结论有一定的差异性，接下来将从库中抽样100余份验证二者的身高估计值与实际身高的误差，以及误差在一定区间的数据占样本总数的百分比。见表格6。

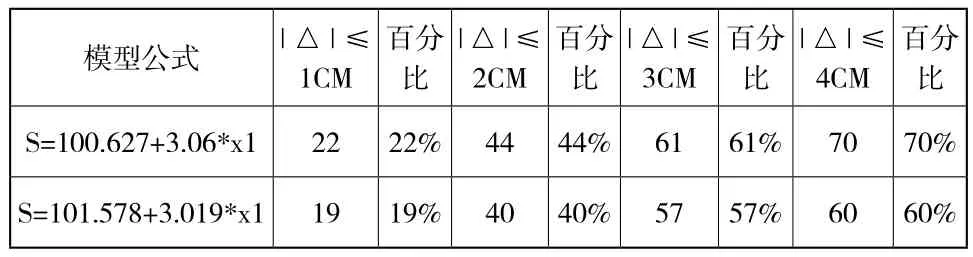
表格6 不同误差范围与百分比的统计结果

经上述分析比较发现，使用第一个模型即使用逐步回归方法得出的效果较好一些，出错率相比较低，说明使用逐步回归得出的回归模型：身高=100.627+3.06*（足跟后缘凸点到拇趾前缘凸点的距离）推算身高的效果较好一些。在结果评价过程中将同一地区的足迹抽样检测发现，逐步回归模型建立的回归方程效果接近于真实身高值。

四、讨论

在实验过程中考虑到人的生活环境、种族、地域等条件的影响因素，本实验基于120份样本研究同质人群、同省份、不同年龄、不同性别的油墨捺印足迹作为研究对象，通过统计软件分析各个测量值与身高之间的关系并建立回归方程，在一定程度上可以为分析推算身高提供较为量化的依据。根据结果统计评价的结果显示，使用该方法测量足长推算身高在小范围的有比较高的准确度。

该实验存在的误差来源分析主要是提取的都是警校大学生的足迹，取样范围相对较狭窄。虽提取的样本是不同年龄，但是年龄的分布均集中在17岁至30岁之间，对于中老年人的同质人群足迹还并未进行统计测量，所以目前系统误差会受到一定的客观制约。

[1]史力民.足迹学[M].北京：中国人民公安大学出版社，2007.

[2]Robbins LM.Footprints collection，analysis and interpretation.Springfield，IL: Charles C. Thomas，1985.

[3]Irene Atef Fawzy，Nashwa Nabil Kamal. Stature and Body Weight Estimation from Various F ootprint Measurements Among Egyptian Population [J]. Forensic Sic，2010，55(4)：884-888.

[4]贾俊平，何晓群，金勇进.统计学[M].北京：中国人民公安大学出版社，20014.

Measure the Bare Footprint Though Using Multiple Regression Method to Analyze Homogeneous Population Height

QIAN Sheng-nan
(National Police University of China，Liaoning，Shenyang，110035)

By selecting 120 bare footprint samples the same areas，different ages and gender，measured respectively the distance of trailing edge pressure bumps to five toe front convex point and the distance of trailing edge pressure bumps into the ball inside and outside convex point.Using SPSS statistical analysis software for data to carry on the multiple regression analysis and stepwise regression analysis，finding there are linear relationship between the seven distance and height，set up corresponding mathematical model and obtained the regression equation，and compared the difference between misjudgment rate and accuracy rate.This is a more reliable and powerful method for using footprint analysis homogeneous population height.

bare footprint; homogeneous groups; analysis height; multiple regression

天下溪）

D918.91

A

2095-1140(2017)05-0033-04

2017-06-21

公安部2016年科技强警基础工作专项项目“足迹步态特征的生物力学基础研究”（2016GABJCD）

乔胜男（1992- ），女，河南灵宝人，中国刑事警察学院2015级痕迹检验专业硕士研究生，主要从事痕迹检验足迹研究；朱玉婷（1991- ），女，重庆人，中国刑事警察学院2015级痕迹检验专业硕士研究生，主要从事痕迹检验足迹研究。