关于行星运动模型疑问引发的思考

孙东振 (厦门一中海沧分校 福建 厦门 361000)

关于行星运动模型疑问引发的思考

孙东振
(厦门一中海沧分校 福建 厦门 361000)

由学生的一个疑问入手，简要分析行星运动模型与双星模型之间的关系.

日心参考系 质心参考系 双星模型

1 提出疑问

高中阶段一般将行星绕恒星运动近似为匀速圆周运动，在讲授“动量守恒定律”这节课时， 有学生发现了一个问题：行星运动模型动量不守恒，以地球绕太阳做圆周运动模型为例，如图1所示，该运动是以地球和太阳之间的万有引力作为向心力，而地球与太阳之间的万有引力是一对相互作用的力，属于内力，若将其他星体对该系统的力忽略掉，那地球与太阳构成的系统应该符合动量守恒定律．由图1可以看出，地球绕太阳转动，系统只有地球存在动量且方向随着圆周运动在不断变化，很显然动量不守恒，那么到底问题出在哪儿呢？

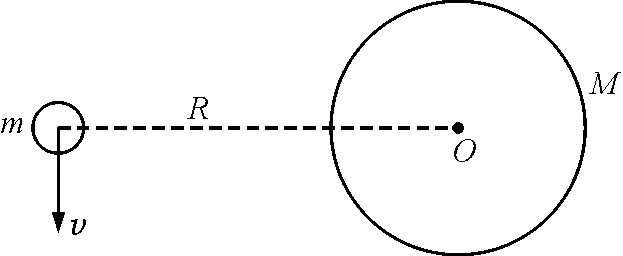
图1 地球绕太阳做圆周运动

2 问题分析与讨论

对于上述问题，笔者起初也是有点迷惑，深入思考之后发现问题出在参考系的选取上．首先我们需要了解，在描述地球绕太阳转动的运动过程中，我们其实默认选取了太阳的中心为参考系，即日心参考系O，而实质上该参考系为非惯性系，变换一下参考系，选取日地系统的质心参考系C(惯性系)，如图2所示．

图2 选取日地系统的质心参考系

以太阳中心为参考系的日心参考系O相对于质心参考系C的离心加速度为aM，则太阳受到的惯性力为MaM，物体受到的惯性力为maM，在日心参考系C中引入惯性力[1]，则有

d(mv)=(M+m)aMdt

(1)

其中v是地球在日心参考系中的速度，可以看出惯性力的存在是日心参考系动量不守恒的原因，式(1)也可以看成是该参考系的动量定理方程．但值得注意的是，虽然对于日心参考系来讲系统动量不守恒，但是角动量确实是守恒的，其原因在于该系统惯性力没有力矩，也不做功．另外需要说明的是这里提到的惯性力指的是惯性离心力，在地球绕月球做圆周运动的理想模型里没有考虑科氏力．

为了更简单地为学生解释，我们可以将日地系统看成双星模型，即选该系统的质心为参考系，如图3所示.

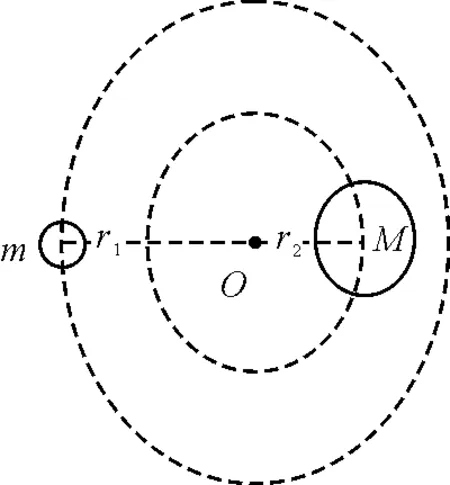
图3 双星模型

则满足

mω2r1=Mω2r2

(2)

v1=ωr1v2=ωr2

(3)

r1+r2=R

(4)

其中，m，M，r1，r2，v1，v2，分别是地球和太阳的质量、轨道半径和线速度.由式(2)～(4)可得

mv1=Mv2

(5)

(6)

式(5)说明在质心参考系中动量是守恒的，所以我们在运用动量守恒定律时是需要考虑参考系的选择问题的.

3 行星运动模型与双星模型的关系

经过以上的讨论我们发现高中阶段学习的双星模型即选择的是质心参考系，那日地系统两种参考系区别有多大呢，对于日心参考系，如图4所示，地球利用其与太阳之间的万有引力做向心力来做圆周运动，则对地球有

(7)

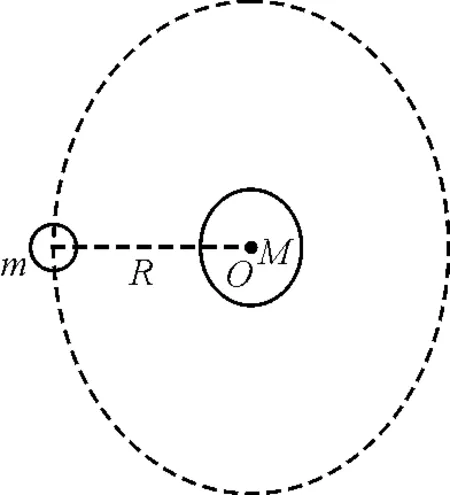
图4 地球以万有引力绕太阳做圆周运动

在质心参考系中对m来分析，如图3所示，应用牛顿第二定律和万有引力定律有

(8)

由(7)、(8)两式有

(9)

又由式(6)可得

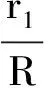
(10)

由于太阳的质量约是地球质量的33万倍，则由(9)、(10)两式可得

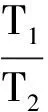
(11)

即对于日地系统来讲，两种参考是近似等价的.

4 结论

由此可以看出，在M≫m情况下，以日心为参考系的行星模型可以看成是以质心为参考系的双星模型的特例，在特定条件下它们是可以相互转化的．实际在太阳系八大行星中质量最大的木星，其质量也不足太阳质量的千分之一，所以尽管日心参考系为非惯性系，但在太阳质量远大于其他行星的情况下，我们也可以近似地将其简化为惯性参考系来研究行星的运动规律．

1 高炳坤，谢铁增.地球所受的一种易被忽视的惯性力.大学物理，1991，10(11)：46～47

2 李铁.非惯性系中的动量定理与动量守恒.电子科技大学学报，2004,33(5):624～626

2017-05-27)