规则模型在大学物理教学中的运用研究*
陈 志
(西北工业大学理学院 陕西 西安 710129)
巩贺贺(西北工业大学软件与微电子学院 陕西 西安 710129)郝丽梅(西安科技大学理学院 陕西 西安 710054)
王海鹏 金克新(西北工业大学理学院 陕西 西安 710129)
规则模型在大学物理教学中的运用研究*
陈 志
(西北工业大学理学院 陕西 西安 710129)
巩贺贺
(西北工业大学软件与微电子学院 陕西 西安 710129)
郝丽梅
(西安科技大学理学院 陕西 西安 710054)
王海鹏 金克新
(西北工业大学理学院 陕西 西安 710129)
在大学物理的教学中,很多物理概念通过简化的模型加以运用.为了更好地适应现在大学物理内容多、学时少的特点,我们通过不断地改革和创新,强调规则模型运用的重要性,通过结合微元概念形成一套有效的教学方法.对该方法通过列举和分析,并用Maple软件再现物理内容的推导演绎过程.
大学物理 规则模型 微元 Maple
1 引言
在大学物理课程中,涉及的定义多、符号多、公式多、理论性强并且较为抽象.学生在学习过程中普遍认为该课程是一门难学的课程.在教学过程中,课程的课时较少,学生在短时间内无法理解这些抽象概念,只能死记硬背,认识不到这些抽象公式的实质含义,不能体会该课程在实际中的具体应用,导致缺乏相应的学习兴趣.
这种现象的产生是各种因素形成的,这对我们的教师来说是一个很大的挑战.与之相反,现实社会中强调的基础研究的原始创新恰恰需要这种基本的推演能力.在2017年的高考考试大纲修订通知中,就明确提高了对基本公式、基本公式的生成过程和推导过程的要求.新时期如何教学生?教学生什么内容?这些对于教师来说都是很值得探索研究的[1,2].
因此,为使大学物理变成一门学生喜欢的学科,为使大学物理这门学科更好地培养学生们的综合能力[3],我们教师任重而道远,必须认真思考对传统教学体系的改进.我们知道在科学研究中,数值计算是一种非常重要的研究方法,该方法首先需要建立模型或者引用他人的模型,然后根据模型编写代码,计算出模拟结果.类似的[4],我们教学中发现借助于这种计算思维可以获得不错的教学效果,利用规则模型的运用的教学方法,能够有效地缓解教师在有限的课时内要完成教学任务,学生普遍感到节奏太快,学习紧张没有更多时间消化吸收知识等问题.
2 大学物理中的规则模型
我们知道,在大学物理中力学和电磁学等内容占了很大的课时,且以刚体中涉及到转动惯量的内容、电磁学中涉及到电场强度和磁场强度的内容较为复杂且学生较难理解.教学中我们发现这些内容使用了相似的物理模型,若再结合大学物理中的微元概念,这些内容就是相同的,讲授的这些知识点学生也比较容易理解和容易接受.我们可将这些模型具体分为两部分,一种是点向纵向发展为主的模型,一种是点向横向发展为主的模型.具体如下.
以纵向为主发展:点、偶极子、直杆、圆柱体(壳)等,如图1所示.
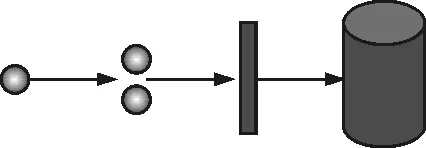
图1 以纵向发展为主模型
以横向为主发展:点、圆环、圆盘、球体(壳)等.

图2 以横向发展为主模型
2.1 规则模型在力学中的运用
转动惯量一直是刚体中的重点和难点内容,一般不规则的物体的转动惯量很难通过简单的分析计算得到,更多的是通过实验来获取.在我们的教材中为了简化求解引入了系列的规则模型及其组合体.这样我们就能够比较方便地计算这些模型所对应的绕定轴的转动惯量.根据前面列举的几大模型,从模型纵向和横向发展来看.现列举几例来说明.
【例1】求质量为m,长为l的均质细杆对图3给定轴的转动惯量.
(1)转轴垂直于杆并通过杆的中点;
(2) 转轴垂直于杆并通过杆的一端.

图3 直杆转动惯量的模型图
解析:建立如图3所示的坐标,在细杆上x处取线元dx.
线元的质量为

细杆过中点的垂直转轴的转动惯量为
并可用类似的方式得出第(2)问的结果

根据该微元方案,利用横向发展的模型,点可以发展为圆环模型.如例2.
【例2】求一质量为m,半径为R的均质细圆环对通过其中心且垂直于环面转轴的转动惯量(图4).
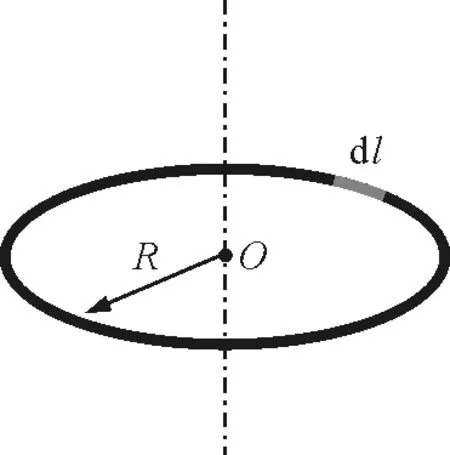
图4 圆环转动惯量的模型图

在圆环上任取长度为dl的线元,该线元的质量为dm=λdl.
由于圆环上各线元到转轴的距离均为R,所以圆环对该轴的转动惯量为
【例3】半径为R,质量为m的均质薄圆盘,求过盘心且垂直于盘面的轴的转动惯量(图5).

图5 圆盘转动惯量的模型图
解析:薄圆盘可以看成是许多半径不同的同心圆环的集合.薄圆盘的质量面密度

任取一半径为r,宽度dr的圆环.圆环的质量为
dm=σ·2πrdr
利用例2结果的微元形式,圆环的转动惯量为
dJ=r2dm=r2·σ2πrdr=2πσr3dr
则整个圆盘对该轴的转动惯量为
按照微元类似的思路,将圆环结果进一步应用到球体中.
【例4】求质量m,半径R的均匀球壳对直径的转动惯量(图6).

图6 球壳转动惯量的模型图
解析:取如图6所示的微圆环,则



根据球壳的结论,加上微元思路可进一步求出球体绕轴的转动惯量.
【例5】求质量m,半径R的均匀球体对直径的转动惯量(图7).

图7 球体转动惯量的模型图
解析:以距中心r,厚dr的球壳为微元,则

根据例4的结果,其微元形式为

但是如果不用以上模型来求解,计算就会复杂得多且涉及到多重积分,也缺少模型间的层次和递进性,短时间内学生难以掌握.
除了这些模型给求解转动惯量带来方便外.基于以上单个模型或其复合模型也可方便地求解其他力学内容.如:单摆、复摆、扭摆等模型相关的力学问题.
2.2 规则模型在电磁学中的运用
前面的一些规则的模型,不但大量地应用在力学中,而且也同样应用在电磁学中,只是需将其中的微元变量dm变为dq而已,同样的模型就可以用来研究电磁学的内容,现运用常见的圆环和圆盘为例子来说明.按照点横向发展可以获得圆环的模型如例6.
【例6】半径为R的均匀带电细圆环,带电荷量为q(图8).求:圆环轴线上任一点P的电场强度.

图8 圆环电场强度的模型图
解析:

dE⊥=dEsinθdEx=dEcosθ
圆环上电荷分布关于x轴对称E⊥=0
由几何关系可以得到

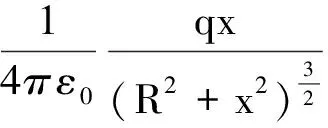
【例7】求面密度为,半径为R的均匀带电圆盘在轴线上任一点的电场强度(图9).

图9 圆盘电场强度的模型图
解析:依题可知
dq=σ2πrdr
微元圆环的电场强度为

基于这些模型及其结论可以进一步地运用到其他内容的模型中,例如平板电容器等知识点中,且这些模型同样适用于磁感应强度的内容.
【例8】半径为R的圆环,通有电流I(图10).求轴线上一点P的磁感应强度.

图10 圆环转动惯量的模型图

根据对称性B⊥=0.



【例9】半径为R的均匀带电圆盘, 带电荷量为+q, 圆盘以匀角速度ω绕通过圆心垂直于圆盘的轴转动(图11).求:圆盘轴线上的磁场.

图11 圆盘磁感应强度的模型图



2.3 Maple实现规则模型在大学物理中的运用
上述的规则模型的运用,为大学物理知识的掌握起到了非常大的促进作用, Maple等软件的运用[5],可以将公用化模型进一步代码化,更易再现公式的推导过程和结果,且相比于手工推导,软件可以更方便地拓展到一般和复杂的模型的公式推演过程,是在有限学时下对大学物理学习的一个有益补充.现列举一简单模型——圆环如表1所示.

表1 圆环中不同物理量的代码推演过程

软件代码J=IntdJdl,l=0..2πR()=IntdJdl,l=0..2πR() Ex=IntdExdq,q=0..q()= IntdExdq,q=0..q()B=IntdBcos(α)dl,l=0..2πR()=intdBcos(α)dl,l=0..2πR()数学表达式 ∫2πR012Rmπdl=R2m ∫q014x(R2+x2)32πε0dq= 14xq(R2+x2)32πε0∫2πR014Iμ0Rπ(R2+x2)32dl=12Iμ0R2(R2+x2)32
从表1可以看出,软件代码及其代码执行的数学表达式和计算结果.我们可以方便地推导和计算圆环所对应的转动惯量、电场强度及磁感应强度等物理量,可见用Maple推导得到的计算结果和流程与人工计算的思维一致,而且这样的流程可以轻易地拓展到更加复杂的模型及计算过程中,只要学生掌握基本的Maple命令,知道简单的微积分知识以及正确的物理原理,就可以做到人人都会的效果.采用该程式计算思维后,一些重复性的工作,显然比人工计算效率高得多,根据需要还可以使公式图形可视化,这对于我们的课程学习甚至是以后的科学研究都大有裨益.更为重要的是我们可以不牺牲教学质量、顺应智能社会和信息社会的前提下,有效地解决学生数学计算能力的不足与教师的课时有限间的不可调和的矛盾,从而真正地体现出通识教育课的价值.
3 结论
大学物理教学中规则模型的运用再结合微元概念和Maple等软件,可以较为有效地解决学生课时短、内容多的矛盾.教授时可以将力学和电磁学等知识点有机地结合起来,方便同学的学习和复习;教师教学的时候,能够更加系统、更加清楚地讲授所对应的知识点;利用Maple软件,通过计算机的可视化可以再现知识点的推演过程,且可进一步拓展到更加复杂的模型的计算.
1 宋士贤.工科物理教程(第3版)教师参考书.北京:国防工业出版社,2008
2 吴百诗.大学物理学(上,中,下).北京:高等教育出版社,2004
3 万珍珠,陈玲,陈洪云. 关于提高大学物理教学效果的探讨.物理通报,2016 (4):18~20
4 陈国良,董荣胜.计算思维与大学计算机基础教育.中国大学教学,2011,1(7):11
5 何青. Maple教程.北京:科学出版社,2006
ApplicationResearchonRuleModeinUniversityPhysicsTeaching
Chen Zhi
(School of Science,Northwestern Polytechnical University,Xi′an,Shannxi 710129)
Gong Hehe
(School of Software and Microelectronics,Northwestern Polytechnical University,Xi′an,Shannxi 710129)
Hao Limei
(School of Science,Xi ′an University of Science & Technology,Xi′an,Shannxi 710054)
Wang Haipeng Jin Kexin
(School of Science, Northwestern Polytechnical University,Xi′an,Shannxi 710129)
In the teaching of college physics, many physical concepts are understood by applying simplified rule model. In order to adapt to many contents and few teaching hours in modern college physics, we stress the importance of application of rules model by reforming and innovating, and an effective teaching method is formed by combining of the differential elements concepts. It is analysis and performed by exact example, and Maple software can deduce the progress of the physics contents.
college physics;rule model;differential elements;Maple
2017-05-08)
*中央高校基本科研业务费项目,编号:3102016ZY027;西北工业大学探究式、研究型课程资金(2015-13)资助;西安科技大学教育教学改革与研究项目,编号:JG1268
陈志(1979- ),男,博士,副教授,研究方向:物理教学研究.

