先张法预应力高强混凝土波形板桩抗弯性能的试验研究

胡少伟, 孙岳阳, 范向前

(1.南京水利科学研究院 材料结构研究所,江苏 南京 210029; 2.河海大学,江苏 南京 210024)

先张法预应力高强混凝土波形板桩抗弯性能的试验研究

胡少伟1，2, 孙岳阳1,2, 范向前1

(1.南京水利科学研究院 材料结构研究所,江苏 南京 210029; 2.河海大学,江苏 南京 210024)

先张法预应力高强混凝土波形板桩是一种新型的预制支护桩。为了了解这种新型桩的受力特性，采用等效截面法计算其抗裂弯矩以及抗弯极限承载力；通过3块相同截面、不同预应力筋试件的抗弯性能试验，研究了这种新型板桩的抗弯破坏现象和力学性能。结果表明：相同截面下，预应力筋根数越多，板桩的抗裂弯矩和极限抗弯弯矩越大；试验结果比等效截面计算的结果偏大，说明采用等效截面法进行结构设计是可行的，并且结构偏于安全。这也验证了等效截面法的合理性。

波形板桩;等效截面;抗裂弯矩;抗弯极限弯矩

目前，常用的基坑支护以及护坡结构主要有现浇钢筋混凝土灌注桩、钢板桩和钢管桩[1]。其中灌注桩需要在现场完成浇注施工，施工工期长，施工成本高；而钢板桩和钢管桩因其耐腐蚀性能较差，只能短期使用，不适合用于大型的水利工程中。预制混凝土桩作为支护结构，已在码头、围堰、河道等边坡支护工程中得到应用；但是预制桩强度低、型号单一、受力性能差，影响了其结构性能。21世纪初，D.A. KORT首先将预应力应用于钢板桩上进行荷载试验，并将试验结果与数值分析结果进行比较，发现预应力能提高钢板桩的整体刚度，从而使桩的屈服荷载显著增加[2]。

先张法预应力高强混凝土波形板桩(简称“波形板桩”)既是预制混凝土桩又是预应力构件，近几年从东南亚国家引进，是一种新型的支护桩，具有挡土面积大、抗弯和抗剪性能强、经济效益好、施工工期短、施工工艺先进等优点。波形板桩采用“U”形截面，如图1所示，单桩挡土面长度为1.0～1.5 m，大大提高了结构刚度，在保证受力性能的同时降低了结构配筋率。史展等将波形板桩和其他类似支护桩型进行了对比，从实际应用出发，总结了混凝土板桩码头在内河软基上应用的优越性以及需要改进的问题[3]。张后禅首次对混凝土波形板桩进行了初步的理论分析，并总结了相应的施工方法[4]。波形板桩不同于矩形桩与管桩，研究起步比较晚，目前，国内外有关波形板桩的试验研究尚不多见，为弥补此缺陷，本文采用波形板桩截面等效原理，通过理论计算与实际试验相结合的方法，研究了波形板桩的抗弯性能。

图1 波形板桩图

1 波形板桩结构设计方法

1.1 截面等效转化

波形板桩的截面形状类似于“U”形，截面的上翼缘和下翼缘主要承担抗弯承载力，截面腹板主要承担抗剪承载力，如果按照“U”形截面计算承载力，则计算过程较为复杂，需通过截面等效方法来简化计算。“U”形截面的受力特点和“工”形截面的受力特点类似，可将截面形式换算成力学性能相对接近的“工”形截面，则需要确定“工”形截面的上下翼缘宽度、上下翼缘厚度、腹板宽度以及截面高度。为保证截面内钢筋保护层厚度和截面有效高度相等，假设“U”形截面的高度、上下翼缘厚度分别和“工”形截面的高度、上下翼缘高度相等。计算抗弯承载力时，还需要保证“U”形截面和“工”形截面的刚度相等以及截面面积相等。等效截面结构如图2所示。

图2 截面等效示意图

图2结构中等效截面的等效计算式为：

2hfbf+(h-2hf)b=A，

(1)

(2)

h=Hu，

(3)

hf=hu。

(4)

试验中板桩“U”形截面宽度为1 000 mm，高度为450 mm，上翼缘宽度为440 mm，上下翼缘厚度为120 mm，截面面积为177 500 mm2，截面惯性矩为3.505×109mm4，通过计算，等效“工”形截面尺寸如图3所示(图中单位为mm)。

图3 等效“工”形截面尺寸图

1.2 力学性能计算

计算波形板桩的承载力时，可以按照等效后的“工”形截面(图3)计算，预应力筋在截面内的位置不变，混凝土保护层厚度不变。

1.2.1 抗裂弯矩计算

依据《混凝土结构设计规范》(GB 50010—2010)[5]，预应力混凝土波形板桩桩身抗裂弯矩计算公式为：

Mcr=[(σce+γftk)]W0。

(5)

式中：Mcr为桩身抗裂弯矩；σce为桩身截面混凝土有效预压应力，板桩预应力中钢筋预应力损失主要考虑张拉锚具变形、钢筋内缩、混凝土蒸汽养护、预应力钢筋的应力松弛以及混凝土收缩和徐变；有效预压应力的计算主要参考文献[5]中的相关规定；γ为混凝土截面抵抗矩塑性影响系数；ftk为桩身混凝土抗拉强度标准值；W0为板桩换算截面受拉边缘的弹性抵抗矩。

1.2.2 正截面抗弯承载力计算

当等效矩形应力图[5]的混凝土受压区高度x在等效“工”形截面的下翼缘中时，即∑σpiApi≤α1fcbfhf，则桩身正截面抗弯弯矩计算式为：

Mu=∑σpiApi(hi-x/2)。

(6)

式中：Mu为桩身正截面抗弯弯矩；σpi为第i排预应力钢筋的实际应力值；bf为等效“工”形截面上翼缘宽度；Api为第i排预应力钢筋的截面积；hi为第i排受拉预应力钢筋距离混凝土受压区外边缘的距离；i为截面所配的预应力钢筋排数；α1为经验系数，取0.98；fc为混凝土轴心抗压强度；x为等效矩形应力图[5]的混凝土受压区高度，按式(7)计算确定，

α1fcbfx=∑σpiApi。

(7)

当等效矩形应力图[5]的混凝土受压区高度x不在等效“工”形截面的下翼缘中时，即∑σpiApi>α1fcBhf，则桩身正截面抗弯弯矩计算式为：

Mu=∑σpiApi(hi-xt/2)。

(8)

式中xt为受压区混凝土重心至受压区外边缘的距离，按式(9)计算确定，

(9)

式中x按式(10)确定，

α1fc[bx+(bf-b)hf]=∑σpiApi。

(10)

按上述公式计算时，混凝土受压区高度应符合下列条件：

x≤ξbh0，

(11)

(12)

x≥2a′。

(13)

式中:ξb为相对界限受压区高度；h0为截面有效高度，即受拉区各层钢筋合力点至截面受压边缘的距离；β1为经验系数，取0.78；εcu为非均匀受压时的混凝土极限压应变，取0.003 3；fpy为预应力筋的抗拉强度设计值；Es为预应力筋弹性模量；σp0为受拉区纵向预应力筋合力点处混凝土法向应力为零时的预应力筋应力;a′为受压区纵向筋合力点至截面受压区边缘的距离。

当x<2a′时，板桩正截面抗弯弯矩按式(14)计算,

Mu=fpy∑Api(hi-a′)。

(14)

2 波形板桩试验概况

2.1 试件参数

本次试验所用的3块波形板桩均由江苏金源管业有限公司提供，截面宽度均为1 000 mm，高度均为450 mm，根据预应力筋的不同可分为A、AB和B型3类，A型波形板桩在上下翼缘分别布置6根直径为10.7 mm的预应力钢棒，AB型波形板桩在上下翼缘分别布置6根直径为12.6 mm的预应力钢棒，B型波形板桩在上下翼缘分别布置8根直径为12.6 mm的预应力钢棒。具体截面如图4所示，参数见表1。

图4 波形板桩截面图(单位：mm)

序号高度/mm厚度/mm宽度/mm长度/mm板型预应力筋横向筋直径/mm有效预压应力/MPa145012010006000A12@10.7mm85.20245012010006000AB12@12.6mm86.95345012010006000B16@12.6mm88.88

本次试验的波形板桩预应力筋均为PC钢棒，其几何特性、力学性能及张拉控制力见表2，混凝土材料性能参数见表3。

表2 预应力主筋几何特性、力学性能及张拉控制力

表3 混凝土力学性能

通过前面1.2节的内容以及波形板桩截面尺寸及材料参数，计算试验所用的A、AB和B3种型号的波形板桩的抗裂弯矩和极限弯矩值，结果见表4。

表4 波形板桩抗裂弯矩、极限抗弯弯矩计算值

2.2 试验方案设计

2.2.1 加载方案

波形板桩的抗弯试验参考《先张法预应力混凝土管桩》(GB 13476—2009)[6]中相关规定，采用简支梁对称加载装置，通过100 t油压千斤顶利用分配梁进行对称加载，支座间距为4 m，分配梁支座间距为1 m，加载示意图如图5所示。

图5 抗弯试验加载装置

图5中:1为分配梁铰支座垫板；2为分配梁固定铰支座；3为分配梁滚动铰支座；4为分配梁；5为波形板桩；6为支墩铰支座垫板；7为滚动铰支座；8为固定铰支座；9为支墩；10为测挠度用位移计。

波形板桩弯矩采用式(15)进行计算,

(15)

式中：M为抗弯弯矩；W为板桩重量；L为板桩长度；P为千斤顶荷载；a为1/2加荷跨距，本次试验中取0.5 m。

抗弯试验加载方案采用分级加载,步骤如下。

第一步：按抗裂弯矩的20%的级差由零加载至抗裂弯矩的80%，每级荷载的持续时间为3 min；然后按抗裂弯矩的10%的级差继续加载至抗裂弯矩的100%，每级荷载的持续时间为3 min，观察是否有裂缝出现，测定并记录裂缝宽度。

第二步：如果在达到100%抗裂弯矩时未出现裂缝，则按抗裂弯矩的5%的级差继续加载至裂缝出现。每级荷载的持续时间为3 min，测定并记录裂缝宽度。

第三步：按抗弯承载力设计值的5%的级差继续加载至出现以下所列极限状态的检验标志之一为止。

1)受拉区混凝土裂缝宽度达到1.5 mm；

2)受拉钢筋被拉断；

3)受压区混凝土破坏；

4)挠度超过设计最大挠度。每级荷载弯矩的持续时间为3 min，观测并记录各项读数。

2.2.2 测点布置

为了获得波形板桩截面在加载过程中的应变以及中性轴的位置变化情况，选取板桩跨中以及加载点下2个截面，由于截面的对称性，取半边截面共布置8个应变片(编号分别为1-1,1-2,…,1-8)，分别位于板桩截面底部、上下翼缘与腹板的交界处、腹板内外侧中间位置，上翼缘上下表面的中部，如图6所示。试验过程中各应变片的数据通过DH3816静态应变采集仪电测获得。

图6 应变测点布置图

试验时为了得到波形板桩的挠度情况，并且进行对比分析校核，在板桩的跨中布置一个位移计，位移计的量程不小于100 mm，测量精度为0.01 mm，位移数据的采集通过静态应变采集仪电测，可以随时调出每级荷载下的荷载-挠度曲线。

3 试验过程及结果分析

3.1 试验过程

综合3块波形板桩的加载过程和破坏形态，3块波形板桩的破坏形式均为抗弯破坏，从加载至破坏主要经历3个阶段：

1)弹性阶段。在施加荷载初期，混凝土未开裂，波形板桩处于弹性状态，混凝土与预应力钢棒之间协同工作良好。

2)裂缝产生阶段。随着荷载的增加，当A型波形板桩的荷载增加到194 kN左右、AB型波形板桩的荷载增加到220 kN左右时，在板桩底部，加载点附近最先产生细微裂缝。当B型板桩荷载增加到288 kN左右时，在板桩底部，跨中附近最先产生细微裂缝。

3)裂缝开展阶段，直至破坏。随着荷载持续增加，在加载点与跨中的纯弯段区域出现新的裂缝，原有的裂缝不断向上发展，裂缝宽度也持续增大。当A型板桩的荷载增加到302 kN、AB型板桩的荷载增加到407 kN、B型板桩的荷载增加到510 kN时，波形板桩受拉区混凝土的最大裂缝宽度达到1.5 mm，标志着波形板桩达到其抗弯极限承载力。以AB型板桩为例，最终破坏时的裂缝分布如图7所示，底部受拉区混凝土裂缝如图8所示。

图7 AB型波形板桩裂缝分布图

图8 AB型波形板桩极限状态桩身裂缝

3.2 试验结果与计算结果对比

表5列出了3种桩型的抗裂弯矩和极限弯矩的实测值、计算值以及二者的比值。通过计算得出，抗裂弯矩实测值与计算值的比值平均值为1.13，极限弯矩试验值与计算值的比值平均值为1.16。总体上抗裂弯矩和极限弯矩的试验值比计算值大，工程上按理论计算值作为设计值进行设计是可行的。如果控制一块矩形板桩和波形板桩截面面积相等、截面宽度相等、材料用量和参数相等，比较它们的极限承载力知，波形板桩的承载力比矩形板桩的要高很多。

3.3 弯矩-跨中挠度曲线

图9为A型、AB型和B型波形板桩抗弯试验过程中典型的弯矩-跨中挠度曲线。

图9 弯矩-跨中挠度曲线

从图9中可以看出：试验开始阶段，3种型号的波形板桩均处于弹性状态，跨中挠度随弯矩的增长基本呈线性关系；当弯矩达到开裂弯矩时，即A型波形板桩弯矩达到140 kN·m左右，AB型波形板桩弯矩达到160 kN·m，B型波形板桩弯矩达到210 kN·m左右时，它们的弯矩-挠度曲线出现明显的拐点；随着荷载的继续增加，跨中挠度增长速度加快，呈现塑性变化；最终达到极限弯矩时，A型波形板桩的跨中挠度为14.9 mm，AB型波形板桩的跨中挠度为13.9 mm，B型波形板桩的跨中挠度为12.9 mm，均小于规范中规定的挠度限值[6]，即计算跨度的1/200，对于本次试验的3块波形板桩来讲，计算跨度的1/200即为20 mm。

一般梁的受弯破坏有2种破坏模式[7]：一种为一般弯曲破坏，另一种为弯曲劈裂破坏。2种破坏模式的典型荷载-挠度曲线如图10所示。

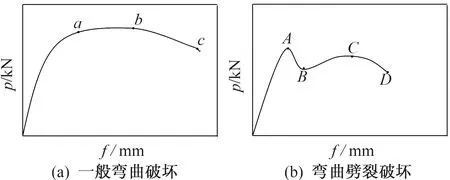
图10 试件弯曲破坏下典型荷载-挠度曲线

由图9结合图10可以看出，本次试验中的3块波形板桩的抗弯破坏属于一般弯曲破坏。由图10(a)可知，荷载初期oa段，混凝土的应力-应变大体呈线性关系；混凝土开裂后，由于桩身中预应力钢棒的存在，能较好地抑制裂缝的发展，板桩的刚度变化不大；但是随着荷载的增加，钢棒开始承受较大的拉力，板桩挠度增长速率加快，裂缝也向板桩上翼缘迅速发展，但荷载仍然可以继续增加；b点对应的荷载为极限荷载，此时应该对应板桩的受压区混凝土被压溃，受拉钢棒屈服；但本次试验中以波形板桩裂缝最大宽度达到1.5 mm为达到抗弯极限承载力的标准，说明3块波形板桩达到极限荷载时处于图10(a)中的ab段，实际试验过程中受压区混凝土未达到极限压应变，还可以继续加载。

3.4 弯矩-应变曲线

图11、图12和图13分别为A型、AB型和B型板桩加载点截面弯矩-应变曲线，图中2-1、2-2、2-6、2-8为应变片编号。

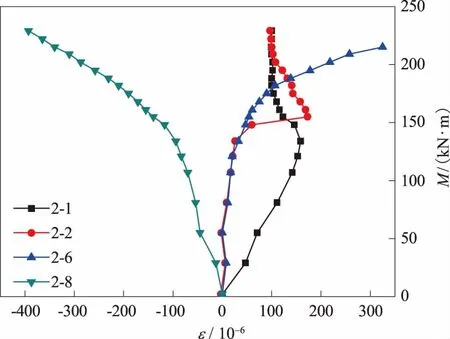
图11 A型板桩加载点截面弯矩-应变曲线

图12 AB型板桩加载点截面弯矩-应变曲线

图13 B型板桩加载点截面弯矩-应变曲线

从图11—13中可以看出，在加载初期，3种波形板桩加载点截面下翼缘的混凝土均受拉，上翼缘混凝土均受压，受拉和受压应变随弯矩的增长基本呈线性关系；随着弯矩的增加，A型板桩的裂缝在加载点附近截面的下翼缘混凝土中出现，裂缝周围的混凝土的应变曲线有一个下降的过程，如图11和图13中的2-1应变曲线，明显出现一个拐点；AB型板桩的裂缝同样在加载点截面的下翼缘出现，应变片由于受拉出现损坏，在混凝土开裂时，混凝土的拉应变为200～300 με；当裂缝产生后，波形板桩下翼缘顶部混凝土的应变随着弯矩的增大迅速增大，如图中的2-2应变曲线，而3种型号波形板桩的上翼缘始终受压，应变随弯矩变化依然呈线性关系；弯矩继续增加，加载点截面的中性轴不断上移，板桩下翼缘底部的混凝土受拉应变开始变小，受拉状态转变为受压状态，如图中的2-6应变曲线；接近破坏时，加载点以及跨中截面的中性轴均上移至波形板桩的上翼缘处，在整个加载过程中，波形板桩的上表面的混凝土始终受压，并未出现压溃的现象，压应变均未达到1 000 με，且均未达到混凝土的极限压应变。

图14—16分别为A型、AB型和B型板桩跨中截面弯矩-应变曲线。

图14 A型板桩跨中截面弯矩-应变曲线

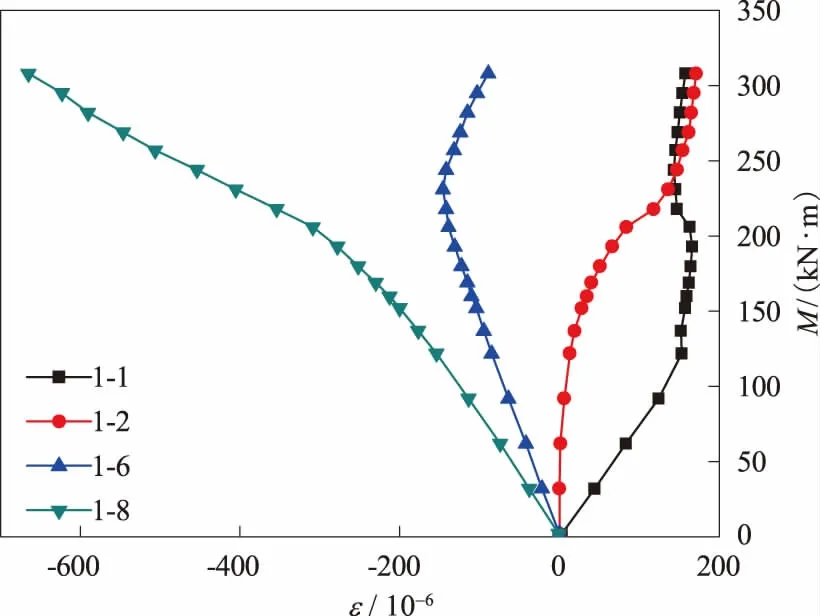
图15 AB型板桩跨中截面弯矩-应变曲线

图16 B型板桩跨中截面弯矩-应变曲线

由图14—16中可以看出，跨中截面弯矩-应变曲线变化趋势基本和加载点截面的相当，因为采用对称加载时，两个加载点之间属于纯弯段，加载点之间的截面弯矩相等。

4 结语

1)试验结果与通过等效“工”形截面计算的结果基本吻合，抗裂弯矩试验值比理论计算值平均提高了13%，极限弯矩试验值比理论计算值平均提高了16%，结构设计时采用该等效办法是可行的，且偏于安全。

2)波形板桩的抗弯试验过程与典型的梁的抗弯试验过程类似，随着荷载的继续增加，中性轴的位置不断上移，在接近破坏的时候，中性轴基本都上移至上翼缘中。在整个加载过程中，板桩的上表面的混凝土始终受压，且均未达到其混凝土的极限压应变。

3)根据试验结果可知，B型板桩的预应力钢棒最粗且数量最多，其抗裂弯矩和抗弯极限弯矩也最大，破坏时的跨中挠度最小，工程中可灵活选用合理的桩型。

[1] 黄志全,李宣,王安明，等．郑州市某建筑深基坑监测[J]．华北水利水电大学学报(自然科学版)，2014，35(1)：51-55．

[2] KORT D A.The transfer matrix method applied to steel sheet pile walls[J].International Journal for Numerical and Analytical Methods in Geomechanics,2003,27(6):453-472.

[3] 史展,林农,郑惠成．混凝土板桩码头在内河软基上的应用[J]．江苏水利，2002(7)：16-17,20．

[4] 张后禅.U形预应力混凝土板桩[J].中国水利,2010(21):67-67.

[5] 中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 50010—2010[S].北京:中国建筑工业出版,2010.

[6] 中国国家标准化管理委员会.先张法预应力混凝土管桩：GB 13476—2009[S].北京:中国计划出版社,2009.

[7] 郑山锁,陶清林,胡义，等．型钢高强高性能混凝土梁抗弯性能试验研究[J]．工程力学，2013，30(3)：140-145．

ExperimentalStudyontheBendingBehaviorsofFirstTensioningPrestressedHighStrengthConcreteCorrugatedSheetPile

HU Shaowei1,2, SUN Yueyang1,2, FAN Xiangqian1

(1.Materials & Structural Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210029, China;2.Hohai University, Nanjing 210024, China)

The first tensioning prestressed high strength concrete corrugated sheet pile is a new type of precast pile. To understand mechanical properties of this new type of pile, the cracking bending moment and bending ultimate bearing capacity were calculated by equivalent section method. According to the bending performance test of three test pieces with same cross section and different prestressed reinforcement, the bending failure phenomenon and mechanical properties of this new type of sheet pile was researched, and the equivalent section method was proved to be reasonable. The results indicate that in the case of equal section areas, the bigger the area and the more the numbers of prestressed steel bars, the cracking bending moment and bending ultimate bearing capacity are greater. The test results are larger than the calculation results by equivalent section method. It is feasible to use this method to design structure and the result is in an over-conservative numeric value.

corrugated sheet pile; equivalent section; cracking bending moment; ultimate bending moment

杜明侠)

TV331;TU473

A

1002-5634(2017)06-0009-07

2017-06-03

国家杰出青年科学基金项目(51325904)；国家重大科研仪器研制项目项目(51527811)；国家自然科学基金项目(51309163,51409162,51679150)；水利部公益性行业专项经费项目(201501035)。

胡少伟(1969—),男,河南杞县人,教授级高级工程师,博导,博士,从事工程损伤断裂、组合结构等方面的研究。E-mail:hushaowei@nhri.cn。

10.3969/j.issn.1002-5634.2017.06.002