水库二维恒定水流的垂向温度分布

韦兵, 朱健

(广西泰能有限公司,广西 南宁 530023)

水库二维恒定水流的垂向温度分布

韦兵, 朱健

(广西泰能有限公司,广西 南宁 530023)

水库水温分布的预测一直是水环境研究的热点问题。水温不仅对水质有重要影响,同时也影响到取水工程的设计。首先通过试验测量了水体密度随水温的变化,结合已有的研究数据,提出了水体密度的计算公式。然后,根据水温层化型水库的流速分布特点,从垂直二维均匀水流和温度模型出发,推导出了一种新的水温垂向分布计算公式,并利用新安江、二滩、Wiwa等5座水库的实测水温资料对其进行了检验,结果表明，精度良好。该公式结构简单,参数意义明确,计算方法简单实用。最后,对温跃层形成的条件进行了讨论。

二维恒定水流；垂向温度;温度分布;水体密度;水库

水温是反映水体状况的重要参数之一。它不仅对电导率、溶解氧、酸碱度、总氮、总磷浓度、藻类密度及浮游植物等产生影响[1-6],而且影响着分层取水利用的工程方案及运行方式[7-8]。因此,掌握水体温度的变化十分重要。

有关水库内水温分布规律的研究起步较早。20世纪70年代,国内学者根据大量的水库水温实测资料总结了一些库内水温分布预测的经验方法,具有代表性的主要有北京水科院朱伯芳法[9]、东北勘测设计院张大发法[10]等。由于经验公式是依据国内外多个水库观测资料获得的,水库的分布范围较广,公式的适用范围亦较广。李怀恩于1993年根据分层型水库的水温分布特点提出了一种垂向水温分布计算公式[11],主要用于月平均水温分布的预测,且计算较为复杂。随着计算方法和计算机技术的快速发展,温度的数值模拟技术得到长足发展,为大型水库和湖泊的温度分层预测提供了众多计算手段,并得到了大量应用[12-19]。但这些数值模型计算复杂,耗时较长,边界条件和初始条件要求较多,因此,仍然需要简单实用的垂向水温分布计算公式对水库的温度分层情况进行快速预测。

本文根据试验数据,研究了水体密度随水温变化的计算表达式,随后结合N-S方程和对流扩散方程,推导出水库水域温度沿水深分布的计算公式。在无温跃层存在的情况下,该公式对温度沿水深分布的野外实测结果有良好的模拟。

1 水体密度随水温的变化规律

对于含沙量较低的清水,水体密度是水温的函数。常压下水体的密度随其温度的变化呈非线性变化：当水温由0 ℃增大到3.98 ℃时,水体密度逐步增大并达到最大值;然后水体密度随水温的继续增加而逐渐降低。

GREENWOOD等于1997年给出了水体密度随水温的变化曲线图[20],笔者将该图数值化后再点绘至图1中。张析于2001年在其著作中列出了水温在0～40 ℃时水体的密度[21],这里也将它们点绘至图1中。另外,为了补充水体密度随水温变化的试验资料,利用5支水银温度计和1支石油密度计进行了实验室测量。5支水银温度计的测量范围分别为：13～17 ℃、18～22 ℃、22～26 ℃、28～32 ℃、35～39 ℃,测量精度均为0.01 ℃。密度计的测量范围为0.950～1.010 g/cm3,测量精度为0.000 5 g/cm3。水体密度随水温变化的试验数据见表1,同样也点绘至图1中。

表1 水体密度随水温变化的试验数据

岳晟于1992年根据试验数据提出的温度计算公式如下[22]：

(1)

式中：T为水温,K;ρ为密度,t/m3。将ρ的单位换算为kg/m3,T的单位换算为℃,则式(1)改写为：

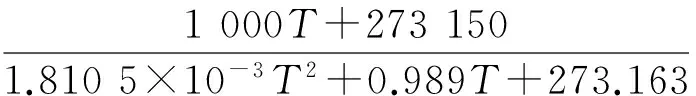
(2)

根据式(2),绘制水体密度-水温曲线，如图1所示。

图1 水体密度与水温的关系曲线

由图1可知,岳晟的计算公式(2)在水温较高时存在明显的误差。

根据笔者的试验数据、张析的试验数据和GREENWOOD等人的曲线图数值化点,利用回归方法得到便于使用计算机计算的公式(3)：

ρ=1 000.2+0.006 7T-0.005 684 55T2。

(3)

2 温度垂线分布公式的建立

2.1 公式推导

从 Navier-Stokes方程和对流扩散方程出发,将方程沿水平方向的单元内积分,通过时均化处理并引入湍流模型,就得到本文将要求解的立面二维方程组：

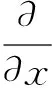
(4)

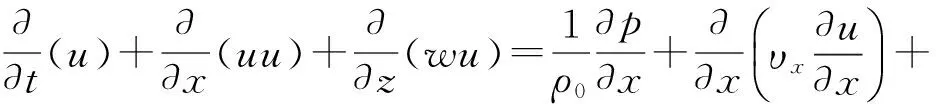
(5)

(6)

(7)

(8)

式中:u、w分别为水平和垂直方向上的流速分量,m/s;p为压力,Pa;ρ0为水的参考密度,kg/m3;υx、υz分别为涡黏性系数分量,m2/s;τwx为边壁阻力,Pa;g为重力加速度,m/s2;kx、kz为水温扩散系数,m2/s;cp为水的比热,cp=4.178 4 kJ/(kg·℃);H为太阳辐射热源项,kJ/(s·m3)；φ0为太阳辐射量,kJ/(s·m3);β为表面水体的热辐射被反射的折减系数,其值随湖泊而变;ξ为太阳辐射在水体中的衰减系数,m-1,取决于水体的浊度等。

对于水深较深、水下地形变化不显著的大型水库,其库区的水流可以近似认为是恒定、立面二维均匀的,从时间平均的角度来看,垂直方向的流速分量为零,即：相当于无流和无风的、水体风平水静的情况。则式(4)—(7)分别简化为：

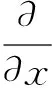
(9)

(10)

p=-ρg(h),

(11)

(12)

式中h为水深,m。

由此可见,对于立面二维均匀流,流速在垂线上的梯度分布对温度的扩散没有影响。由式(8)和(12)可得：

(13)

当水体表层与大气交界面的热量达到平衡时,水体各层的温度将不再发生变化,此时∂T/∂t=0,T(t,0)=T0,则有

(14)

求积分可得：

(15)

式中C为常数。令α=(1-β)φ0/cpρ0,上式可改写为：

(16)

假设水温扩散系数kz为常数,求积分得：

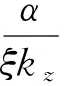
(17)

式中C2为常数。

在水底取绝热条件,则有∂T/∂zz=-h=0,由式(16)可得：

C=αe-ξh。

(18)

对于水体表层,z=0,T(t,0)=T0。由式(17)可得：

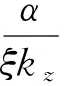
(19)

将式(18)和(19)代入式(17),可得温度的垂线分布为：

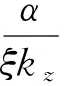
(20)

水体间的相互混合是水体单元相互掺混的过程,包括分子扩散、紊动扩散、剪切离散等。紊动扩散往往是占主要地位的动力。根据实测资料及理论分析,可以认为水温垂向扩散系数kz与水流动量交换中的紊动涡度ε成正比,即kz=λε。这里,λ为常系数;ε的取值可以采用Kajiura假设[11],有ε=κU*h,故有：

kz=λκU*h。

(21)

式中：κ为卡门常数,可取κ=0.41;U*为摩阻流速,m/s。

2.2 公式验证

为了检验水温垂向分布计算公式(20)的可靠性,笔者根据千岛湖不同位置的水温垂向分布的测量资料[19],利用式(20)进行计算。限于篇幅,将部分结果绘于图2。

图2 千岛湖不同位置垂向断面上的实测水温与计算水温

四川二滩水库的库区长136 km,平均水面宽约400 m,最大水深约190 m,是一个典型的狭长的河道式深水库。水库枯季最高水位为1 200 m,电站引水口高10 m,底部高程为1 128 m,在汛期多余弃水经溢洪道和深孔下泄。图3比较了不同日期距大坝700 m处垂向断面上实测水温和计算水温的分布。由图3可知：在3月间二者吻合较好,4月和5月由于水库调度较频繁,模拟精度降低；对比4月和5月的模拟可知,虽然气温升高使表层水体温度得以提高,但由于大坝的泄水,上游来流出现温度均匀的水体被直接带到坝下,向下的温度传递被抑制。

作者分别于2017年2月24日和5月9日利用上海水琛科技服务有限公司的水深水温自动同步测量仪(A型)对百色水利枢纽坝前的水温分布进行了测量。该仪器的深度测量精度为0.02 m,温度测量精度为0.02 ℃。图4比较了本次实测水温和计算水温的垂向分布：二者吻合得均较好；5月9日的实测点与计算曲线的偏离反映出水库调度和风生流对温跃层的影响；2月24日的实测点与计算曲线的偏离主要反映出水库调度对温跃层的影响。

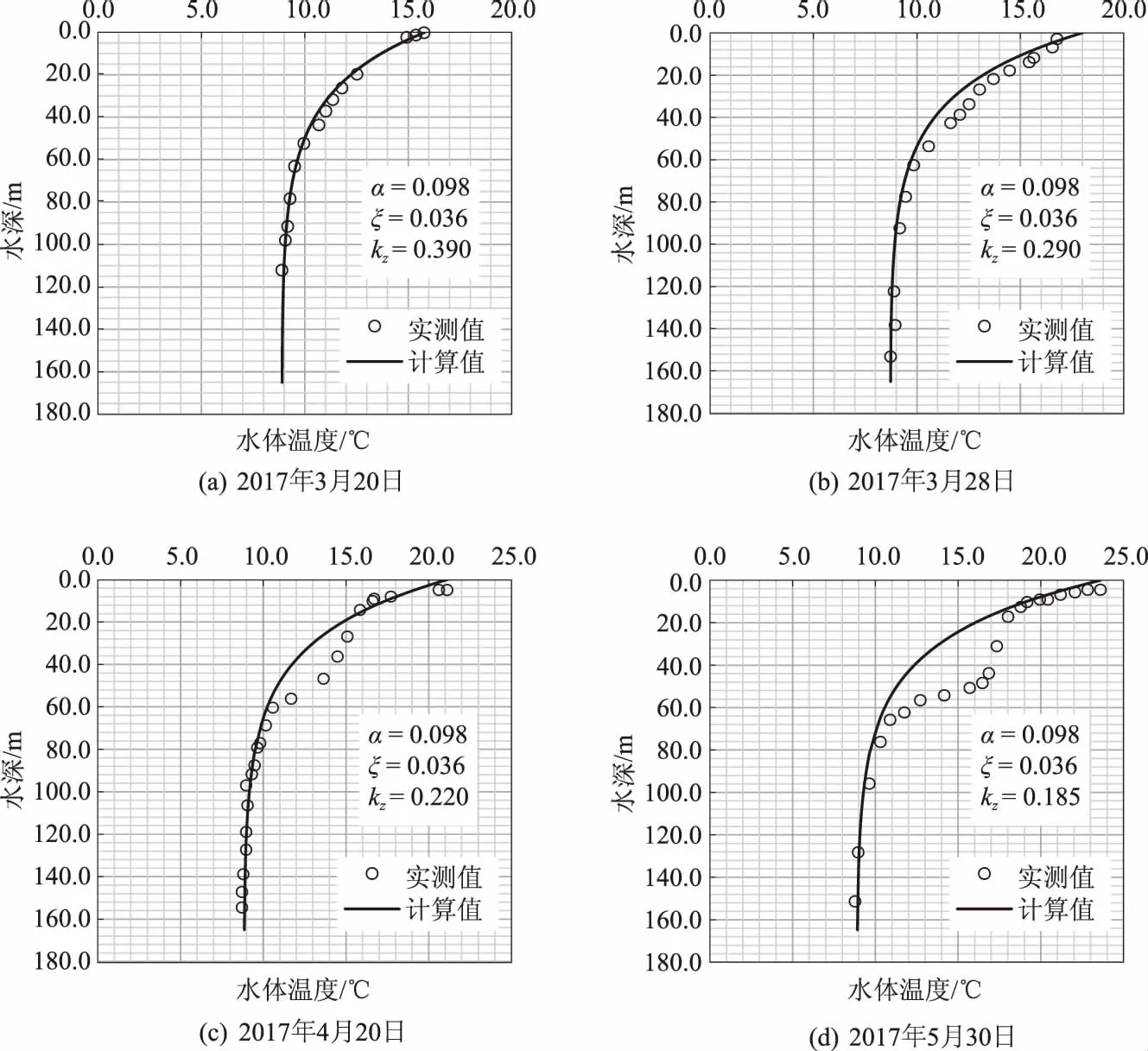
图3 二滩水库距大坝700 m处垂向断面上的实测水温与计算水温

图4 百色水利枢纽坝前水温垂向分布的实测值与计算值

3 讨论

3.1 水库温度的最大变化速度

垂线上水体温度的变化速度可以表达为：

(22)

(23)

由此可见,参数α实际上为当地水体温度的最大变化速度,取决于水体的浊度太阳辐射量、表面水体的热辐射热被反射的折减、水的比热和水体的密度等。对于水体中不同的垂线位置,其值的变化幅度可能较小,但不同水库其值不同。从上述计算可知,表层水的最大变化速度约为0.095～0.120 ℃/s。

3.2 垂直水温分布的影响参数

由式(20)可见,影响垂直水温分布的参数有3个,除表层水的最大变化速度α以外,kz受水体的掺混强度和水深的影响。它不仅是一个重要的指标,而且对于水体中垂线位置不同和水库调度的不同,其值的变化幅度可能较大。表示太阳辐射在水体中的衰减系数ξ取决于水体的浊度,对于水体中不同的垂线位置,其值的变化幅度可能相对较小,主要是随湖泊种类而变。

此外,对于水体的表面温度T0,如果缺乏实测资料,依据笔者的工程经验,则可用相应的气温平均资料来预测。如预报月平均水温的垂线分布,则在夏季可用预报日前30 d的平均气温减去5 ℃来预测,在冬季则减去2～3 ℃。

3.3 水体的热吸收与热释放现象

水体温度升高来源于表面热辐射,表层水体的温度向下传递,温度总是从高的地方向低的地方传递。因此,当水体表层温度不断降低时,水体向大气中释放热量;当水体表层温度不断升高时,太阳通过大气向水体内输送热量。当垂线上实际温度位于此平衡分布温度线右边时,水体温度将具有升高的趋势。反之,当垂线上实际温度位于此平衡分布温度线左边时,水体温度将具有下降的趋势。

3.4 水体的温跃层现象

从上述垂向二维恒定水流情况下的温度分布可知,水库水温沿垂向一般只存在指数型分布,形成稳定的温跃层的情况很少。当上游来流为温度均匀的水体时,由于水库泄水而一直维持在水库中而成为一个温跃层。否则,如果存在温跃层,只可能是附近均匀温度的水团入侵,或者垂线上存在流速反向的水体,该二元流的对流与扩散均匀化了该层水体的温度。由此可见,水库湖泊中风生垂直环流是形成温跃层的因素。这一点在图5的示例中得到很好的佐证[23]。图5为日本Miwa水库在1959年7月25日13:00到15:00的水温观测结果,风向由13:00的NNW转到16:15的N,即由断面B吹向断面A,风速由13:00的3.34 m/s减弱到16:15的1.14 m/s。由于断面A靠近大坝,实测到水库内垂直面上存在一个风生环流,且断面B到A之间的表层水体行进到坝前下潜进入底部再向上游断面B运动。因此,流场分布是制约温度分布的重要因素,只有准确计算流场,才可能正确计算出温度的分布。

图5 Miwa水库的水温垂线分布的测量值与计算值

4 结语

本文补充了水体密度随水温变化的试验数据,并提出了水体密度计算的简便公式,计算结果可靠。从垂向二维恒定水流的情况出发,推导了温度垂线分布的计算公式,野外观测结果验证了该公式具有良好的精度。研究表明：在该理想流态下,温度分布呈指数形式,水体表层温度最高;当上游来流为温度均匀的水体时,由于水库泄水而一直维持在水库中而成为一个温跃层;否则,只有当垂直面上存在风生环流等二元流或者上游来流而出现温度均匀的水体时,水体中才会出现温跃层;流场分布是制约温度分布的重要因素,只有准确地计算流场,才可能正确计算出温度的分布;影响温度垂线分布的主要因素有最大变化速度、温度扩散系数及太阳辐射在水体中的衰减系数。

[1] 胡水景.深水湖泊溶解氧值稳定性探讨[J].干旱环境监测,2001,15(2):62.

[2] 王君波,彭萍,马庆峰,等.西藏玛旁雍错和拉昂错水深、水质特征及现代沉积速率[J].湖泊科学,2013,25(4):609-616.

[3] 卢金锁,李志龙.热分层对水库水质的季节性影响:以西安黑河水库为例[J].湖泊科学,2014,26(5):698-706.

[4] 袁琳娜,杨常亮,李晓铭,等.高原深水湖泊水温日成层对溶解氧、酸碱度、总磷浓度和藻类密度的影响:以云南阳宗海为例[J].湖泊科学,2014,26(1):161-168.

[5] 艾海男,夏洪薇,胡学斌,等.深水湖泊氮和磷沿水深的分布特性[J].中国环境科学,2015,35(10):3085-3089.

[6] 牛远,孔祥虹,余辉,等.抚仙湖夏季热分层时期浮游植物空间分布特征[J].生态学杂志,2016,35(7):1865-1871.

[7] 高学平,陈弘,李妍,等.水电站叠梁门分层取水流动规律及取水效果[J].天津大学学报(自然科学与工程技术版),2013，46(10):895-900.

[8] 王海龙,陈豪,肖海斌,等.糯扎渡水电站进水口叠梁门分层取水设施运行方式研究[J].水电能源科学,2015(10):79-83.

[9] 朱伯芳.库水温度估算[J].水利学报,1985(2):14-23.

[10] 张大发.水库水温分析及估算[J].水文,1984(1):21-29.

[11] 李怀恩.分层型水库的垂向水温分布公式[J].水利学报,1993(2):43-49.

[12] 胡振红,沈永明,郑永红,等.温度和盐度分层流的数值模拟[J].水科学进展,2001,12(4):439-444.

[13] 邓云,李嘉,李克锋,等.紫坪铺水库水温预测研究[J].水利水电技术,2003,34(9):50-52.

[14] 邓云,李嘉,李克锋,等.梯级电站水温累积影响研究[J].水科学进展,2008,19(2):273-279.

[15] 任华堂,陈永灿,刘昭伟.三峡水库水温预测研究[J].水动力学研究与进展,2008,23(2):141-148.

[16] 伍悦滨,徐莹,田禹,等.磨盘山水库温度场的数值模拟[J].哈尔滨工业大学学报,2010,42(6):925-928.

[17] 张少雄.大型水库分层取水下泄水温研究[D].天津：天津大学,2012：36-87.

[18] 杨惠敬,魏杨,郑西来.青岛市王圈水库温度场数值模拟[J].中国海洋大学学报(自然科学版),2014,44(6):85-89.

[19] 白杨,张运林,周永强,等.千岛湖水温垂直分层的空间分布及其影响因素[J].海洋与湖沼,2016,47(5):906-914.

[20] GREENWOOD N N,EARNSHAW A.Chemistry of the Elements[M].2nd ed.Oxford:Butterworth-Heinemann,1997:620-631.

[21] 张析.实用化学手册[M].北京:科学出版社,2001:415-421.

[22] 岳晟.水的密度随温度的变化[J].大学化学,1992,7(3):53.

[23] HORIUCHI S,AMBEY.The currents and the distribution of the temperature of water in Miwa reservoir[J].Geography,2008,34(5):268-279.

VerticalTemperatureDistributioninReservoirswithTwo-dimensionalSteadyFlows

WEI Bing, ZHU Jian

(Guangxi T-energy Engineering Consulting Co., Ltd., Nanning 530023, China)

The temperature of water in reservoirs not only affects the water quality, but also influences the water intake design. Hence, prediction of water temperature distribution in reservoirs is always a hot topic in water environmental research. In this paper, the change of water density with water temperature was investigated experimentally. Afterwards, a formula was derived to predict the water density at a temperature based on the previous studies. Then, a new formula of vertical water temperature distribution was deduced from the combination of two-dimensional flow model and water temperature model, which was validated successfully by the data collected in five reservoirs, such as Xinanjiang reservoir, Ertan reservoir and Wiwa reservoir. The formula is simple, the parameters have explicit meaning, and the method is easy and practical. Finally, the formation of thermocline was discussed.

two-dimensional steady flow; vertical temperature; temperature distribution; water density; reservoir

陈海涛)

TV137

A

1002-5634(2017)06-0082-06

2017-06-12

国家科技重大专项项目(2017ZX07206)。

韦兵(1964—),男,广西南宁人,高级工程师,从事泥沙运动力学、水环境学、水资源等方面的研究。E-mail:496922532@qq.com。

朱健(1975—),男,广西玉林人,高级工程师,从事水资源管理、水环境治理等方面的研究。E-mail:13877107846@139.com。

10.3969/j.issn.1002-5634.2017.06.013