初探基于核心素养下的数学作业设计

秦奋

（安徽省安庆市开发区实验学校）

初探基于核心素养下的数学作业设计

秦奋

（安徽省安庆市开发区实验学校）

学科教学是培养学生核心素养的根本途径，而作业设置是数学教学的重要环节.优化作业设置，是培养学生核心素养的有效手段.文章从知识性、差异性、精炼性三个方面论述基于核心素养下的数学作业设计思想.

学科教学；作业设置；核心素养

随着基础教育改革的不断深入，培养学生的核心素养是我们教育工作者所面临的一个新的课题.在初中阶段，笔者认为数学学科核心素养的培养主要通过学科教学来完成，有以下四个环节，即课前备课、课堂教学、作业设置和课后辅导.而合理的作业设计对巩固课上所学知识，形成技能、技巧，培养学科核心素养，提高学生学习能力，有着十分重要的作用.但目前大多数学校的学生作业由原来的练习本转化为配套的练习册，教师大多地让学生从第几页做到第几页，学生作业的难度和深度一下子上升到中考的要求，导致大多数学生苦不堪言.不论优等生、学困生，不论省示范、普通学校，不论城市、乡村，……所有的教师布置同样的作业，所有的学生做同样的作业.学生的个体差异得不到尊重，因材施教的原则没有落到实处.为此，笔者结合自身的教学实践探索，围绕作业设计的基本原则谈谈自己的做法.

一、关注知识性

这里的关注知识性有三重意思：第一，关注数学的核心知识，使学生在完成作业的过程中回顾所学的基础知识，提炼出基本的数学思想方法；第二，作业的设计一定要从学生的认知水平出发，以学定“问”；第三，要立足于“四基”，即基础知识、基本技能、基本思想、基本活动经验，注重通性、通法.

当然，教师可根据自己的教学进度，从课后习题、练习册或其他资料中选取合适的习题，让学生通过练习训练既能达到所期望的目标，又能把握合适的度，而且不额外增加学生的负担，的确需要教师自身有很好的业务功底，而且需要教师对初中数学教材的体系，《义务教育数学课程标准（2011年版）》（以下简称《标准》），近几年中考的方向和学科的核心素养，都能做到心中有数.教师在设置知识性的作业时还要有一定的梯度，这种梯度可以体现在对某一道题从简单到复杂的问题呈现，也可以体现在对某一知识点的从易到难训练题的设置，让学生脚踏实地往前走，激发其学习的潜能，体会到学习数学的乐趣.

案例1：在“三角形的中位线”的作业设置中，笔者设置了如下两道题.

（1）如图1，读句画图.

①延长AB到点D，使BD=AB；

②反向延长线段CA到点E，使AE=2AC；

③连接DE，并猜想线段BC和DE的关系.

（2）已知：如图2，两个共用一个顶点的等腰直角三角形ABC、等腰直角三角形CEF中，∠ABC=∠CEF=90°，连接AF，M是AF的中点，连接MB，ME.

图1

图2

①当CB与CE在同一直线上时，求证：MB∥CF；

②若CB=a，CE=2a，求BM，ME的长.

【设计意图】第（1）小题是概念题，只要学生理解了中位线的概念画出图形就可以解决（画出图形如图3所示），第（2）小题学生就要稍作思考了.这两道题的知识性很强，反复运用中位线的知识，达到巩固和提升课堂教学的目的.第（2）小题第①问稍微简单些，但也需要作辅助线.如图3，延长AB至点D，得B为AD的中点.因为M是AF中点，所以BM为△ADF的中位线.故MB∥CF.同理，第②问也要延长FE，CA交于点G，证EM∥GA，且因为且BC=BE=a，所以即BM=EM=

图3

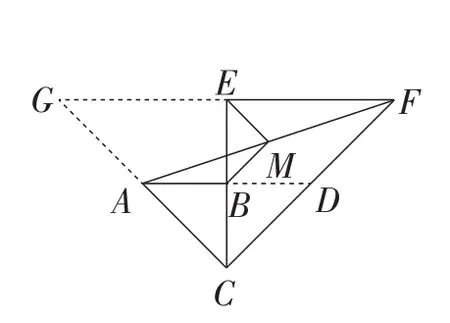
图4

这两道题的设置从易到难，循序渐进，基本上让学生理解和掌握了三角形中位线的教学内容.如果再布置一些其他没有选择性的习题，笔者认为就是学生的负担了，收效也甚微.

二、关注差异性

大教育家孔子说过，中人以上，可以语上也；中人以下，不可以语上也.即孔子教人，因材施教.由于学生是一个个独立的个体，每个孩子成长的环境和从小所受的教育不同，学生之间的数学知识和数学能力的差异是客观存在的.《标准》中也明确指出，数学课程应致力于实现义务教育阶段的培养目标，要面向全体学生，适应学生个性发展的需要，使得人人都能获得良好的数学教育，不同的人在数学上得到不同的发展.所以教师在教学中必须按照不同类型学生的认知规律和心理特征，设计出不同的、适合各类学生的作业，从而帮助不同层次的学生都能有效地完成作业，通过不同层次的练习达到最佳的学习效果.

案例2：以“勾股定理”的分类作业为例加以说明.

基础类作业：

（1）在△ABC中，∠C=90°.

①若a=5，b=12，则c=____；

②若a=7，c=4，则b=____；

③若a∶b=3∶4，c=15，则a=____；

④若∠A=30°，BC=2，则AB=____，AC=____.

（2）已知：如图5，在△ABC中，∠C=60°，∠B=45°，

图5

①求BC的长；

②求△ABC的面积.

（3）查阅资料，搜集勾股定理的证明方法.

【设计意图】通过这一类作业的完成，使学生了解勾股定理，体会勾股定理的证明思路和方法，并会运用它解决一些简单的实际问题.

提高类作业:

（1）已知：在Rt△ABC中，两边长分别是6和8，则△ABC的面积为（）.

【设计意图】受思维惯性的影响，此题学生考虑问题不全面，容易出错.因此，通过作业的练习，来培养学生发散思维的能力.

（2）如图6，在Rt△ABC中，∠C=90°，∠A=30°，AC=3，折叠该纸片，使A，B两点重合，折痕与AB，AC交于点D，E，求DE的长.

图6

解：设CE=DE=x，

则AE=3-x.

因为∠A=30°，

所以AE=2DE，

即3-x=2x.

得x=1，即DE的长为1.

【设计意图】此题旨在培养学生运用所学知识解决实际问题的能力.

拓展类作业:

（3）如图7，在长方形ABCD中，AB=6，BC=8，将长方形ABCD沿CE折叠后，使点D恰好落在对角线AC上的点F处，求EF的长和四边形ABCE的面积.

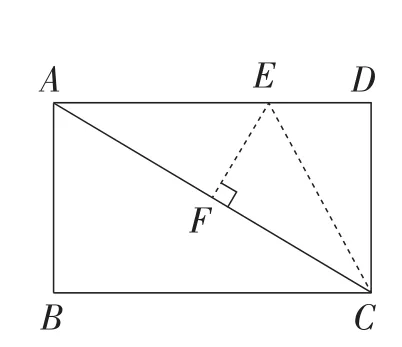
图7

解：设DE=x，AE=8-x，

由折叠得△CDE≌△CFE.

得CD=CF=6，DE=EF=x.

由勾股定理，得AC=10.

所以AF=4.

在Rt△AEF中，因为AE2=AF2+EF2，

所以(8-x)2=42+x2.

解得x=3.

所以EF=3.

【设计意图】这道题旨在加强知识之间的联系，培养学生综合运用所学知识的能力，适合基础比较好的学生.

在本节课的教学中笔者精心选择不同的题组作为配套练习，让每位学生得到不同程度的提升.

三、关注精炼性

有调查数据表明，数学作业大多是机械的训练，一半以上的作业是重复的.70%的学生认为数学作业主要是做练习题或练习册，缺乏创造性和趣味性成为当前困扰学生课后作业的一大难题.教师也清楚，重复的、机械的练习对学习质量的提高作用有限，但不这样做，教师也不放心，唯恐自己的课上所教内容得不到巩固，所学知识点学生没有掌握，达不到自己想要的效果.因此，学生的学习时间绝大多数困于大量重复、机械的作业中难以自拔，而对知识和技能的掌握反而下降，更谈不上培养数学学科的核心素养了.这就要求教师在作业内容的设置上要几经思考，选择有代表性、典型性的题目，在作业的数量设置上要少而精，尽量避免重复、烦琐的计算.

案例3：在“一元二次方程的解法”一课的教学中，笔者设计了这样一道作业题.

用四种方法解方程x2-6x+9=(5-2x)2.

解：（方法1：直接开平方法）原式得(x-3)2=(5-2x)2.

得x-3=±(5-2x).

解得x1=2，

（方法2：配方法）原式整理为3x2-14x+16=0.（方法3：公式法）原式整理为3x2-14x+16=0.

解得x1=2，

【设计意图】在学习一元二次方程解法时，学生往往感到枯燥和乏味.笔者用这样一道简单的一元二次方程，即复习巩固了一元二次方程的三种解法，又让学生对一元二次方程的这三种解法有了清晰的理解和掌握.

总之，学科教学是培养学生核心素养的根本途径，我们必须以学生为中心，以课堂为平台，以作业为载体，才能充分发挥学科的育人功能，提升学生的核心素养.为了实现这一基本理念，我们必须改变传统的作业设计方式，关注学生核心素养的培养和能力的提高，积极主动地去适应社会发展的需要.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版，2012.

［3］张奠宙.解放思想，也来说说数学核心素养［J］.中学数学教学参考（上旬），2017（4）：2，12.

2017—09—12

秦奋（1974—），女，中学高级教师，主要从事初中数学课堂教学研究.