双足机器人的两种步态规划的解耦分析及比较

任 杰，许江淳，岳秋燕，余丽玲

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

双足机器人的两种步态规划的解耦分析及比较

任 杰，许江淳，岳秋燕，余丽玲

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

在双足机器人行走步态规划的研究中，首先对前进方向和侧面摆动进行解耦，建立运动学数学模型，运用 ZMP稳定性判据作为双足机器人行走稳定性判断标准，利用时序构造函数法和三次样条插值法对双足机器人运行步态进行规划。利用matlab软件编程和仿真，能够体现出不同规划方法下步行状态在时间和空间的特征，仿真结果对比表明，利用三次样条插值法的步态规划，能够更好的反映出双足机器人的步行稳定性。

双足机器人; 时序构造函数; 三次样条插值; 步态规划

0 引言

现如今对双足机器人的研究热度变得越来越高，对比轮式或履带式机器人，平面双足机器人更能反映出色的稳定性和可控性，其高度的拟人特性使得双足机器人能够广泛应用于工业制造、教学科研、生活娱乐、医疗康复等领域。而双足机器人是一个高阶、强耦合、非线性的复杂系统，其行走时的步态规划是双足机器人的关键技术之一[1]。本文应用时序构造函数法和三次样条插值法对双足机器人的步态进行规划，进行运动解耦分析，并对比不同步态规划方法的优势劣势，以及他们对双足机器人的运动情况的影响，并在此基础上进行双足机器人的稳定性分析。

1 双足机器人模型的建立

广义坐标法是一种广泛适用的分析方法，它可以用最少的参数和较为统一的方式来描述系统，应用起来较为方便直观，而且可以与许多重要概念及方程的使用相结合。采用广义坐标法对双足机器人进行建模时，可以参照人类下肢的结构和运动特点。经过对比和分析，设定双足机器人的小腿和大腿各为一根密度均匀的刚体连杆，每根连杆之间可活动的连接部分即为运动关节。在踝关节设置两个旋转自由度，以实现脚面的前向俯仰和侧向翻转；髋关节设置三个旋转自由度，分别实现大腿的前向俯仰、侧向翻转和竖直方向的旋转；膝关节参考人类膝关节的前进方向转动的特点，只设置一个旋转自由度，可以实现小腿的俯仰运动。这样双足机器人一共有12个旋转自由度[2]。

双足机器人的运动是一个在三维空间内的立体运动，因此不能只简单将双足机器人看成是平面的单一方向的运动。但考虑到双足机器人立体运动的复杂性，和广义坐标法建模特点，在分析双足机器人运动情况时可将其运动按照三个方向进行解耦，即分解为沿前进方向x轴运动的前向运动、沿着同前进方向垂直平面内y轴方向的往复摆动，以及沿着竖直方向 z轴的起落运动[3]。通过对整个运动的解耦，可以从三个方向更好的表现出运动的特点，便于进行分析和对比。

双足步行机器人的运动学建模分为正运动学建模和逆运动学建模。正运动学建模的部分就是给定双足机器人一个参考坐标系，通过机器人各刚体杆件之间的几何关系和运动情况来确定双足机器人的各关节相对于参考坐标系的位姿[4]。如图 1所示为双足机器人的前进方向建模。

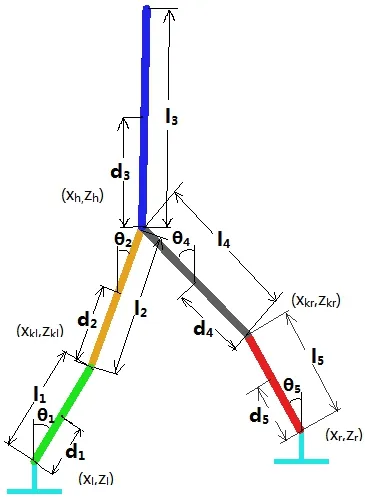
图1 双足机器人前进方向运动模型Fig.1 The motion model of biped robot in forward direction

设定双足机器人的支撑脚踝关节位置为参考坐标的原点，大腿和小腿各为长度为li,(i=1,2,3,4,5)的连杆，则可以在前进方向内得到以下各关节坐标：踝关节坐标(xl,zl)和(xr,zr)，膝关节坐标(xkl,zkl)和(xkr,zkr)，双足机器人运动过程中假设其身体平面始终保持和前进方向垂直，则髋关节坐标为(xh,zh)。在前进方向运动平面内，踝关节和y轴方向夹角分别为θ1和θ5，髋关节处两条大腿和y轴方向夹角分别为θ2和θ4，因不分析上半身双臂和双手的运动情况，则可以将上半身视为一个密度均匀的质量块，也和下肢一样等同为一个密度均匀的摆动刚体连杆，其和y轴方向的夹角为θ3。那么髋关节坐标和摆动腿踝关节坐标可以通过几何关系，由以下的式子表示：

各关节在前进方向的运动速度可以通过对位置坐标的积分来求得，髋关节和摆动腿踝关节的速度可以表示为：

设每段连杆的质心处到各自连杆下端旋转关节位置的长度为di,(i=1,2,3,4,5)，则可以通过几何关系得出各连杆的质心坐标：

通过对以上各式的求导进而可以求得各连杆质心的速度和加速度。

双足机器人的逆运动学分析就是通过步态规划得到机器人的髋关节和摆动腿踝关节与参考坐标之间的相应位姿，进而求取各关节相的实际运动情况。通过关节和连杆间的几何关系，加上一些约束条件，限制关节的运动范围，就可以求得期望解[5]。各关节的求解如下列方程所示：

由于膝关节各只有一个前向运动的转动自由度，只能实现小腿的俯仰，则双足机器人在与前进方向相垂直平面内的运动，即侧向运动的正、逆运动学分析就相对简单一些。如图2中所示的双足机器人侧向运动模型。

图2 双足机器人侧向运动模型Fig.2 Lateral motion model of biped robot

侧向运动建模时是从背离而去的方向为正视方向，以支撑腿踝关节为参考坐标原点。为了便于分析，假设在侧向运动过程的投影中，两条腿是保持平行的，那么两条腿踝关节和髋关节的侧向摆动角同 y轴方向的夹角均相等，则有 θ7=θ8=θ9=θ10，由双足机器人侧向运动的各杆件和关节的几何关系可以得出：基于上述分析，双足机器人的数学模型得以建立。

由此可以得出机器人的侧向转角为：

2 双足机器人的稳定性判据

传统的对运动物体的稳定性分析是通过判断该物体的重心是否落在与地面接触的平面范围内，即静止或匀速运动时，机器人的重心投影点Center of Gravity (COG)落在脚部与地面支撑面内，则机器人稳定。由于双足机器人在运动过程中不可忽略速度的变化，即不可忽略加速度对步行姿态的影响[6]，那么在进行稳定性分析的过程中应该将重力和惯性力考虑在内[7]。对于此问题，南斯拉夫科学家于上世纪 60年代提出了零力矩点 Zero Moment Point(ZMP)稳定性判据[8]，即重力和惯性力的合力在地面上的投影，在这一点的合力矩为零的那一点，如图3所示，若落在双足与地面支撑面所构成的多边形内，如图4所示，则机器人行走稳定，也就满足了双足机器人的动态稳定性。

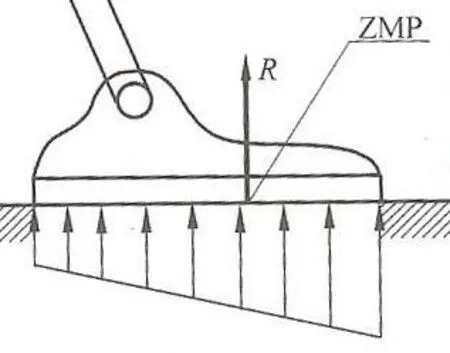
图3 零力矩点判据示意图Fig.3 Zero moment point stability criterion diagram

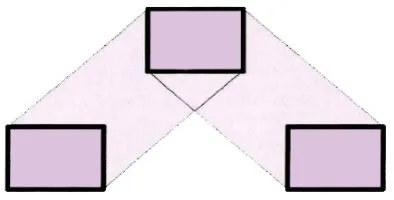
图4 稳定运动时零力矩点的落点区域Fig.4 ZMP possible point of landing area in stable movement

在对机器人进行解耦分析过程中，可以得到零力矩点的坐标公式：

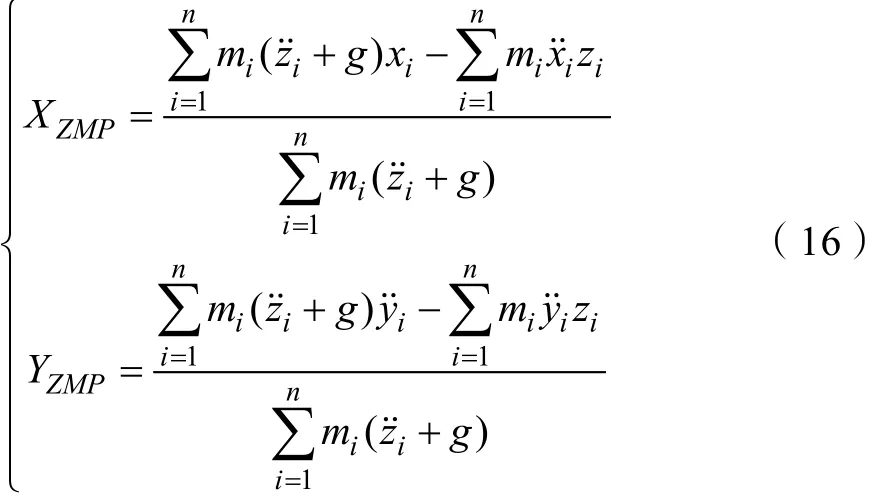
由于零力矩点最终要落到x,y平面内，则z方向的零力矩点为0。通过上面的公式可以求得ZMP点的坐标，并可以通过ZMP点和支撑区域的最短距离来判断稳定裕度。

3 双足机器人运动的步态规划

表1 踝关节和髋关节在步行中的关键位置列表Tab.1 Table of key locations for walking on ankles and hips

在运动过程中，设单步运动的距离为Dt，整个单步运动周期 Tw为单脚支撑期 Td与双脚支撑期 Ts的和。由于机器人通过连杆和关节相连，只要确定踝关节和髋关节的轨迹，就可以确定其他关节的运动轨迹。

3.1 时序构造函数规划法

时序构造函数法的步态规划思路如图5所示。

由于在步行过程中摆动腿和地面发生磕碰引起的振动容易对步行稳定性造成较大影响，在此假设摆动脚每次接触和离开地面时速度为 0，加速度为0，并将此运用到髋关节的运动中[9]。首先构造出双足机器人髋关节的加速度在x方向随时间变化的轨迹函数：

步态是双足机器人运动时各个关节在时序和空间上的一种协调关系，由各个关节运动的一组时间或空间轨迹来描述。起步阶段时，由双脚并立的无初始位移和速度的状态，运动到具有平稳周期步行的中步阶段，该运动阶段是一个过渡阶段；中步阶段是双脚往返交替运动，具有周期性运动特点的阶段；止步阶段是由中步降低速度直至双脚平稳站立，和起步阶段刚好相反。观察步行状态，起步和止步阶段是中步阶段的特例，运动幅度较小，而中步运动阶段具有周期性和代表性，仅需分析中步运动阶段中的单步运动，也就是从摆动脚离地开始到摆动脚再次离地为止的过程，反映为单脚支撑期间的步行姿态。步行运动的代表性位置如表1所示，其位置可以作为后续步态规划的关键位置。通过对上式积分以及初始时刻的加速度为0的条件可以得到髋关节速度随时间变化函数：

图5 时序构造函数法步态规划流程图Fig.5 Flow chart of gait planning of sequential constructor method

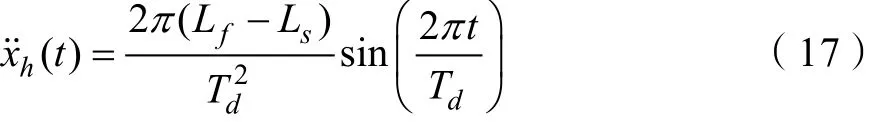
通过对上式积分以及初始时刻的加速度为0的条件可以得到髋关节速度随时间变化函数：

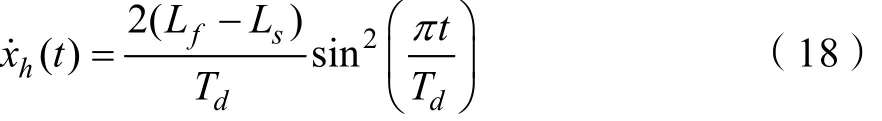
通过对上式积分以及初始时刻的速度为0的条件可以得到髋关节位移随时间变化函数：

由于在z方向的运动是先抬起后落下的运动，则整个步态规划分为(0,Td/2)和(Td/2,Td)两个时段，初始条件依然适用，在(0,Td/2)时段构造出双曲机器人髋关节在上升时的加速度在 z方向的随时间变化的轨迹函数：

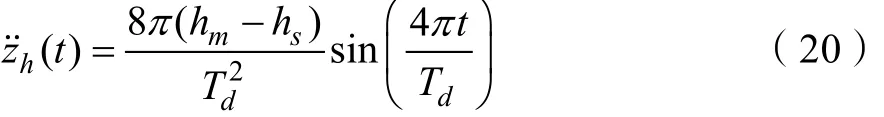
通过对上式积分以及初始时刻的速度为0的条件可以得到髋关节位移随时间变化函数：

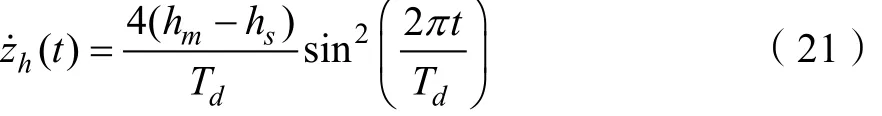
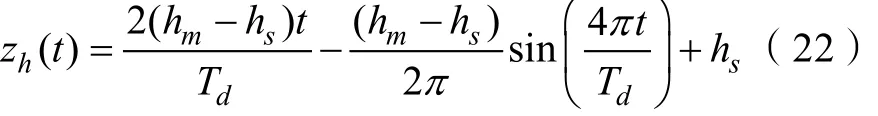
同样的方法，在(Td/2,Td)时段通过构造和积分得出下落时的速度、加速度、位移在 z方向随时间变化的轨迹函数：

由双足步行时关节运动时序的一致性，摆动腿踝关节在运动过程中也遵循初始和中止速度和加速度为0的情况，那么根据上述方法可以构造出摆动腿踝关节运动随时间的轨迹。

3.2 三次样条插值规划法

三次样条插值方法在进行步态规划时，通过用摆动腿髋关节的x和z方向的相对位置来表示运动状态，进而继续确定机器人各部分相对运动的关系[10]。三次样条插值法设计思路如图6所示。

图6 三次样条插值法步态规划流程图Fig.6 Flow chart of gait planning of Cubic spline interpolation

在三次多项式中三个插值点的选取上，由运动的对称性，和位移曲线连续且光滑的特点，选择髋关节的起始位置、最高位置和中止位置，设定关系如下：

由三次样条插值函数的连续性以及其导数的连续性[12]，可得到如下方程：

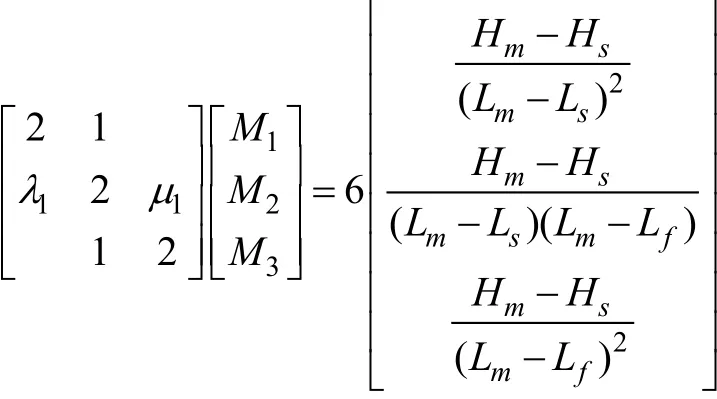
通过追赶法[11]求出 M1,M2,M3的值并代入三次样条函数中，可以得到髋关节的x和z方向的关系表达式：

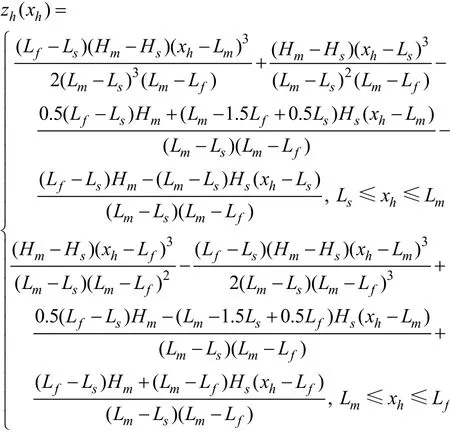
通过对上式的求导，可以得出髋关节的高度变化率相对于位移的情况。并且可以通过类似的步骤，求得踝关节的x方向、z方向的位移、速度和速度变化率同髋关节x方向位置的情况。

4 仿真结果

通过第2节建立的数学模型和第3节设定的两种步态规划方法，按照身高185cm的人体特征，和一定的比例，选取腿长、腿部质量等适当的参数进行仿真。参数选取如表2所示。利用时序构造函数法规划步态，在matlab上进行编程仿真，在单脚支撑期间，髋关节前进方向的仿真结果如图7、图8、图9所示。

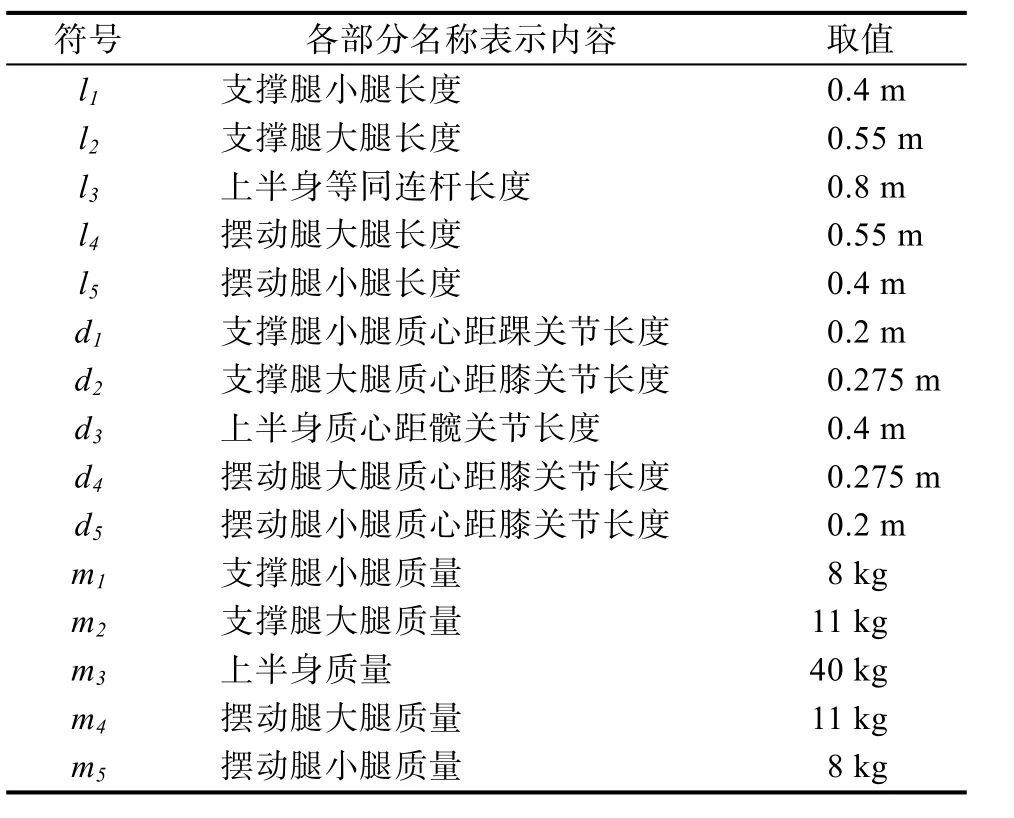
表2 双足机器人各部分参数取值表Tab.2 Table of parameters in each part of the biped robot

时序构造函数法可以较为清晰地表现出髋关节沿行进方向和竖直方向的位移、速度、加速度随时间变化的特征。以上三幅图的(a)部分均为行进方向，即x方向随时间的变化情况；(b)部分均为竖直方向，即 z方向随时间的变化情况。经过对比不难发现，时序构造方法对各关节进行步态规划时，可以保证位移、速度、加速度随时间变化的函数是连续的，且满足初始条件要求，即摆动脚离地和触地瞬间，速度和加速度均为0。

时序构造函数法还可以较为清晰地表现出各关节角度随时间变化的情况。图10所示就是以踝关节和髋关节为例，单脚支撑期间，关节角速度、角加速度随时间的变化曲线。可以发现，角速度和角加速度曲线均连续，但在最高位置交替时，因为步态规划中抬脚和落脚的相反对称特性，整体走势出现较大变化。

三次样条插值法所表现出的仿真结果更具有空间性，如图11(a)所示为单脚支撑期间三次样条插值法规划下的髋关节z方向位移随x方向位移变化曲线，可以较为清晰地反映出双足机器人在空间内的运行姿态，相比较时序构造函数法，更能体现真实的运动轨迹。图11(b)和图12分别为髋关节z方向随x方向位移变化曲线的一阶导数和二阶导数，可以看出三次样条插值法规划的步态具有很高的对称性，且在二阶导数图像中可以明显发现其线性特征。如果需要将时序构造函数法改变成为能反映空间运动姿态的方式，需要首先用时间 t来反映位移、速度及加速度。但是由于x方向运动表达式属于超越方程，无法得到反函数，所以基于求得反函数带入到 z向关于时间 t表达式的方法就无法进行，那么在空间运行姿态方面，也就无法利用对时序构造函数法进行改造而与三次样条插值法对比。

但通过对zmp公式进行改造成空间表达式，再转换到利用时间 t表示的方式，可以进行两种步态规划效果的对比。图13能够清晰反应双足机器人的步态规划稳定性特点，经过对比发现，两种方法计算出来的ZMP轨迹都始终徘徊在重心附近，且利用三次样条插值法的 ZMP轨迹幅度比时序构造函数法的幅度更小，则稳定裕度相对较大，稳定性能更好。

图7 髋关节x、z方向位移随时间变化曲线Fig.7 Displacement curves over time of jip joint in x and z direction

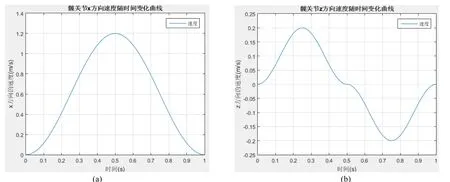
图8 髋关节x、z方向速度随时间变化曲线Fig.8 Speed curves over time of hip joint in x and z direction

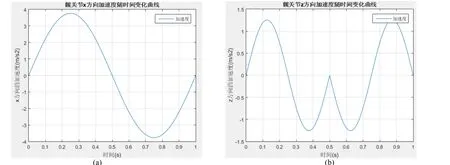
图9 髋关节x、z方向加速度随时间变化曲线Fig.9 Acceleration curves over time of hip joint in x and z direction

图10 踝关节和髋关节各角速度、加速度随时间变化曲线Fig.10 Angular velocity and Angular acceleration curves over time of hip joint and ankle joint

5 结论

本文通过运用两种不同的方法对双足机器人运动进行了规划，从时序构造函数法上能够表现出运动状态随时间的变化；从三次样条插值法上能够表现出竖直方向随着前进方向移动的空间姿态。两者反映出了步态规划的不同特点，但从稳定性的对比上，在相同的参数取值情况下三次样条插值法规划的步态运动稳定性较好，且三次样条插值方法步态规划的结果更能反映出关节角在空间运动的轨迹。但是解耦规划带有一定局限性，在matlab仿真中虽能观察位移、速度、加速度随时间的轨迹或空间的运行姿态，但并不能够很好的反映出运动合成的效果。而解耦规划后的整合运动也是双足机器人仿真运动需要后续研究的侧重点。

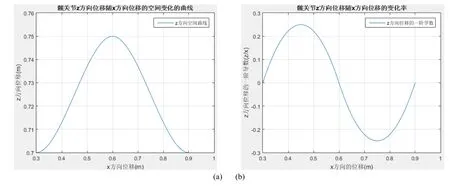
图11 样条插值法z方向位移、x方向位移及一阶导数曲线Fig.11 The cubic spline interpolation z-direction displacement, x-direction displacement and the first derivative curve

图12 三次样条插值法z方向位移和x方向位移二阶导数曲线Fig.12 The cubic spline interpolation z-direction displacement and x-direction displacement second derivative curve

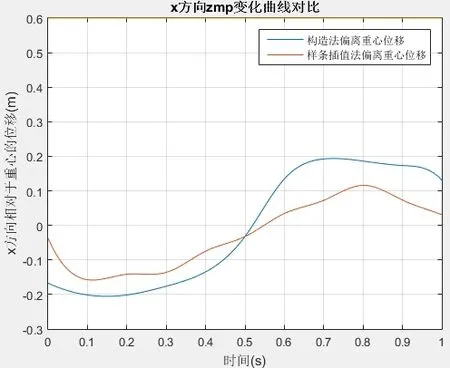
图13 两种方法ZMP对比曲线Fig.13 ZMP comparison curves for both methods

[1] 田彦涛, 孙中波, 李宏扬. 动态双足机器人的控制与优化研究进展[J]. 自动化学报2016. 8(8): 1142-1157.

[2] 康少陈. 基于ADAMS的双足机器人步态规划及仿真研究[D]. 哈尔滨: 哈尔滨理工大学, 2012. 3.

[3] Qiang Huang, Kazuhito Yokoi, Shuuji Kajita, ec al. Planning Walking Patterns for a Biped Robot[J]. IEEE Transactions on robotics and automation, Vol.17, No.3, 2001. 3.

[4] 贺凯, 李韶杰, 古亚威, 等. 移动机器人新型半智能路径导航系统的设计与实现[J]. 软件, 2013, 34(04): 1-6.

[5] 年士瑞. 双足人形机器人多目标步态规划的研究[D]. 合肥: 合肥工业大学 2011. 4.

[6] 吴俊. 六自由度双臂机器人动力学分析与运动控制[J]. 软件, 2017, 38(03): 128-132.

[7] 包志军，马培荪，仝建刚. 人行走速度规律的实验研究[J].实验室研究与探索 2000, (6): 39-42.

[8] Fujita M, Kuroki Y, Ishida T, et al. Autonomous behavior control architecture ofentertainment humanoid robot SDR-4X[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2003. 960-967.

[9] 邓欣. 双足机器人步行稳定性研究[D]. 哈尔滨: 哈尔滨工程大学 2007. 2.

[10] 杨东超,汪劲松.基于ZMP的拟人机器人的步态规划[J].机械工程师 2001.11 23(6):50-55

[11] 于洋, 袁建华, 钱江, 等. 新边界条件下的三次样条插值函数[J]. 软件, 2016, 37(02): 25-28.

[12] 钟兴志, 王晨升, 刘丰, 等. 步态识别综述[J]. 软件, 2013,34(04): 160-164.

Decoupling Analysis and Comparison of Two Gait Planning for Biped Robot

REN Jie, XU Jiang-chun, YUE Qiu-yan, YU Li-ling
(Kunming University of Science and Technology, Faculty of Information Engineering and Automation, Kunming 650500, China)

In the research of biped robot gait planning, firstly, the forward direction and lateral swing are decoupled, and then the mathematical model of kinematics is established. The ZMP stability criterion is used to judge the walking stability of biped robot. Gait planning of biped robot is carried out by using the sequential constructing method and the cubic spline interpolation method. Using MATLAB programming and simulation, by which can reflect the different characteristics of the walking state in time or space under different planning methods. The simulation results show that the gait planning of the cubic spline interpolation method can better reflect the walking stability of biped robot.

Biped robot; Sequential constructing; Cubic spline interpolation; Gait planning

TP242

A

10.3969/j.issn.1003-6970.2017.12.003

本文著录格式：任杰，许江淳，岳秋燕，等. 双足机器人的两种步态规划的解耦分析及比较[J]. 软件，2017，38（12）：10-17

国家自然科学基金项目资助(61363043)

任杰(1989-)，男，硕士研究生，主要研究方向：嵌入式技术及应用，双足机器人步态优化。

许江淳(1962-)，男，副教授，主要研究方向：嵌入式技术及应用。