基于分布估计算法的多目标优化

高 尚，刘 勇

（1. 江苏科技大学计算机科学与工程学院，江苏 镇江 212003；2. 人工智能四川省高校重点实验室，自贡 643000）

基于分布估计算法的多目标优化

高 尚1，刘 勇2

（1. 江苏科技大学计算机科学与工程学院，江苏 镇江 212003；2. 人工智能四川省高校重点实验室，自贡 643000）

论述解决多目标优化问题的若干解法，为了提高多目标优化算法的收敛性和求解精度，提出了一种分布估计的多目标优化算法。给出了3个典型的测试函数的pateto解集。通过4个测试函数测试，并与非劣排序多目标遗传算法(NSGA-Ⅱ)和规则模型分布估计算法（RM-MEDA）两个算法进行了比较。测试结果表明，该算法具有良好的收敛性和分布性，并且效果稳定。

多目标优化；分布估计算法；收敛性

0 引言

在科学研究、工程实践和社会生活中多目标优化问题(multi-Objective optimization problems，简称MOPs)很常见。多目标优化问题的各个子目标之间是相互矛盾的，一个子目标的目标函数提高有可能会引起另一个或者另几个子目标的目标函数性能下降，也就是说要同时使多个子目标目标函数同时达到最优值是不可能的，因此求解多目标优化问题存在一定的难度。对于多目标优化问题，一个解对于某些目标来说可能是较好的，而对于其他目标来说可能是较差的，因此只能在它们中间进行折中权衡和协调，使各个子目标都尽可能地达到最优化。存在一个折衷解的集合称为帕累托最优解集(Paretooptimal set)或非支配解集(nondominated set)。对于多目标优化问题来说，目前一般通过加权等方式转化为单目标优化问题，然后用数学优化方法来求解，但每次只能得到一种权重情况下的最优解，无法得到最优解集。而且多目标优化问题的目标函数和约束函数可能是非线性、不连续的或不可微，传统的数学优化方法往往效率低下，甚至失效。本文试图采用分布估计算法来改善其性能，得到Pareto最优解集。

1 多目标优化问题的数学模型及解法

多目标优化问题含有n个决策变量，m个目标变量，多目标优化问题可表示为

求解多目标优化问题的算法研究目前很热门。目前解多目标优化问题的算法分为两大类：传统优化算法和智能优化算法。传统优化算法有加权法、层次优化法、约束法和目标规划法等。传统优化算法实质上就是将多目标优化问题转化为单目标优化问题，通过采用单目标优化的方法达到对多目标函数的求解，这些算法往往只能得到一个解而非Pareto最优解集。这样得到的解往往与想要得到的最优解集相去甚远，远远满足不了现代工程实践的应用要求。智能优化算法通过对自然现象的仿真模拟，建立在生物智能或物理现象基础上的随机搜索算法。智能优化算法具有自组织、自适应、自学习性等特征，为解决复杂的工程问题提供了重要的技术方法。智能优化算法还具有较高的并行性，一次运行可以求得多个Pareto最优解，具有传统算法不可比拟的优势。因此随着信息技术的进步尤其是智能化技术的进步，各种智能算法的出现，使得利用更加科学合理的智能优化算法成为发展趋势。解多目标问题的智能优化算法目前有进化算法（Evolutionary Algorithm, EA）、遗传算法（Genetic Algorithm，GA）、人工模拟退火算法（Simulated Annealing，SA）、蚁群优化算法（Ant Colony Optimization, ACO）、粒子群优化算法（Particle Swarm Optimization, PSO）、人工免疫系统（Artificial Immune System, AIS）[1]和分布估计算法（Estimation of Distribution Algorithm，EDA）[2]等。

2 分布估计算法的多目标优化

2.1 基本分布估计算法

分布估计算法[3-6]的概念最初由Muhliebe H, Paass G在1996年提出的，分布估计算法在传统的遗传算法基础上发展起来的一种全新的随机优化算法。在传统的遗传算法中，用若干个种群（编码）表示优化问题的一组候选解，种群中的每个个体都有相应的适应值（目标值），然后根据适应值（目标值）大小进行选择、交叉和变异等模拟自然进化的操作，反复进行，对问题进行求解；而在分布估计算法中，没有传统的交叉、变异等操作，取而代之的是概率模型的学习和采样，分布估计算法通过一个概率模型表示候选解在空间的分布，采用统计学习手段从群体宏观的角度建立一个描述解分布的概率模型，然后根据概率模型随机采样产生新的种群，选择优秀种群，估计概率模型，如此反复进行，实现种群的进化，直到满足终止条件。根据概率模型的复杂程度以及不同的采样方法，分布估计算法发展了很多不同的具体实现方法，但是都可以归纳为下面两个主要步骤：首先通过对种群的评估，选择优秀的个体集合，建立解空间的概率模型；然后由概率模型随机采样产生新的种群，一般采用蒙特卡罗方法，对概率模型采样得到新的种群。

在遗传算法中，计算适应值的大小，适应值大的解将以较大的概率进行复制，而分布估计算法直接挑选优秀的个体，避免漏掉一些优秀的个体；遗传算法的交叉和变异可能会破坏已经进化好的个体，而分布估计算法利用“建立概率模型”和“采样样本”两大操作取代了遗传算法中的“选择操作（复制操作）”、“交叉操作”和“变异操作”，以一种带有“全局操控性”的操作模式解决了遗传算法存在的这个缺点。而且分布估计算法不需要太多的参数设置，编程比遗传算法简单。

图1 基本分布估计算法的步骤Fig.1 The flowchart of EDA

分布估计算法的基本步骤如下（如图1所示）：

步骤1 在解空间内按均匀分布随机产生N个点（解），组成初始群体；

步骤2 根据适应值评价函数（目标函数）计算群体中的各个解的适应值，同时保留最好解；

步骤3 根据适应值，选出适应值较好的m个个体组成优势群体；

步骤4 根据优势群体的数据，估计优势群体的概率分布模型；

步骤5 根据估计的概率模型进行随机采样，产生N个新个体，组成新的种群；

步骤6 若满足某种停止准则，则算法结束，群体中的最好个体就是优化的结果；否则算法转到步骤2继续执行。

2.2 解多目标优化问题的分布估计算法

随着分布估计算法的发展与应用，该算法在解决一些实际问题时表现了优越性能，一些基于分布估计算法思想的解多目标优化问题的算法也相继被提出来。Khan等学者将非劣排序多目标遗传算法（NSGA-II）中的选择策略和贝叶斯优化算法(BOA)结合起来，提出了多目标贝叶斯优化算法(mBOA)，取得了比NSGAII更好的效果。Laumanns等学者把SPEA2和 BOA结合起来，用于解决多目标背包问题，效果很好。Zhang和Zhou等学者提出的规则模型分布估计算法（RM_MEDA），该算法是比较经典的分布估计算法求解多目标优化问题的算法，效果令人满意。

正态分布（normal distribution）是一个在数学、物理及实际工程等领域都非常重要的概率分布。大自然界中很多随机变量的概率分布都可以近似地用正态分布来描述。

由概率论知识可知，均值μ，方差σ的估计值分别为：

由计算机仿真理论可知,设 u1和 u2是两个独立的[0,1]区间内的均匀分布随机数，那么同时可以产生2个正态分布 X ～ N(μ, σ2) 的随机数为：

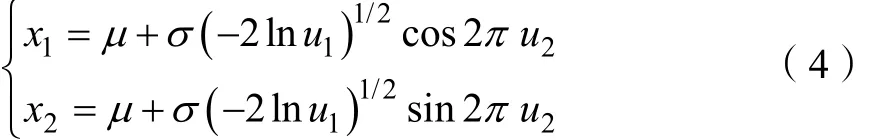
这里给出一种基于正态分布的分布估计算法的多目标优化算法，其步骤如下：

步骤2 计算N个种群的不同目标函数的适应值；

步骤3 根据不同的目标函数，选出各自适应性最好的m/p个解（假设有p个目标函数），构成子群体m个（m＜N，一般m/N比例为0.4左右），并将其中的非劣解保留至下一代，若有相同的解则只保留一个；

步骤4 根据挑选的m个优势个体信息，按正态分布公式（2）和（3）估计每个变量均值ˆiu和方差ˆiσ；

步骤 5 从构建的正态分布概率模型中按公式（4）进行随机采样，得到N个新解，构成新的种群；

步骤6 若达到算法的终止条件则结束（如达到规定迭代次数nmax），否则执行步骤2。

3 算法测试

这里选择了3个典型的测试函数组进行实验，算法的群体规模为N=100，m=40，进化100代，其pateto解集如图2、图3和图4所示。

测试函数1：

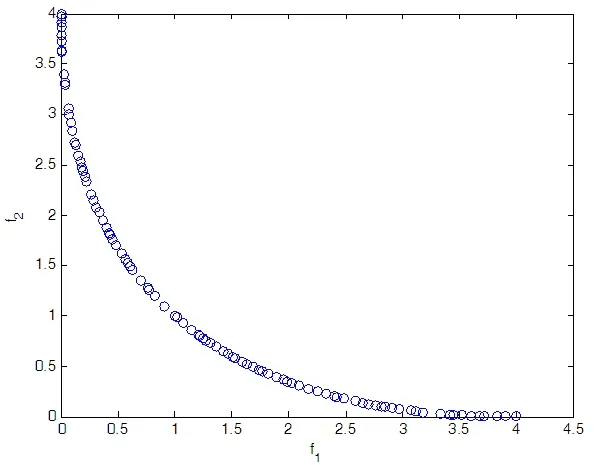
图2 测试函数1的pateto解集Fig.2 Pareto-optimal set of test function 1

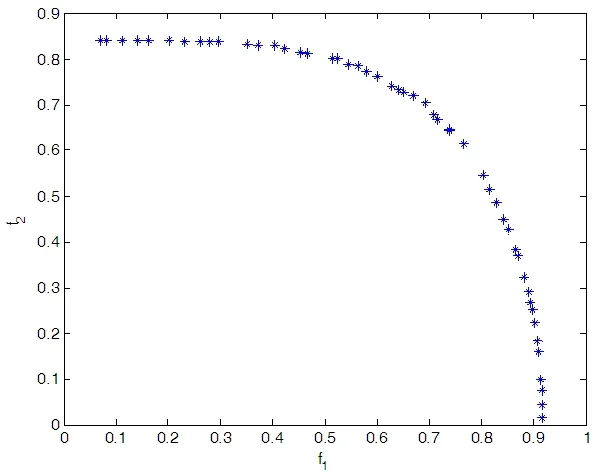
图3 测试函数2的pateto解集Fig.3 Pareto-optimal set of test function 2

为了说明本文算法的有效性，选取典型的测试函数 ZDT1、ZDT2、ZDT3、ZDT6作对比测试，使用文献[7]中的多样性指标：均值和方差，对算法求得的非劣解集进行对比评价，并将本文算法与文献[7]中的非劣排序多目标遗传算法( nondominated sorting genetic algorithm II，NSGA-II)，此算法是采用实数编码，文献[8]的规则模型分布估计算法（RM-MEDA）进行比较，如表1所示。这里NSGA-II的实验结果来自文献[7]，RM-MEDA的实验结果来自文献[8]和本文算法的实验结果是用 Matlab语言编程运行获得。

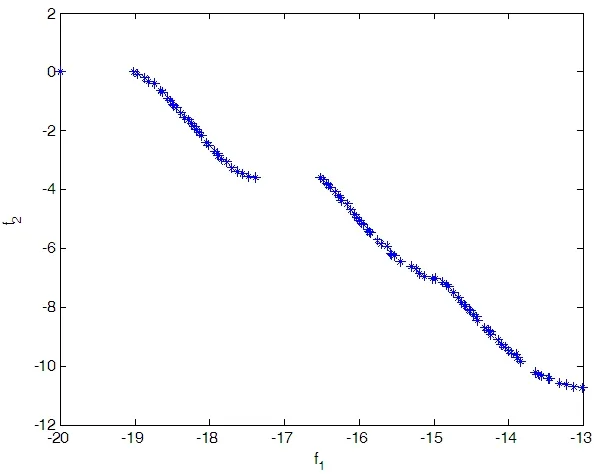
图4 测试函数3的pateto解集Fig.4 Pareto-optimal set of test function 3

表1 均值和方差Table 1 The mean and variance

4 结束语

本文提出了一种分布估计的多目标优化算法，根据每个目标函数挑选若干个解组成种群，然后进行估计概率分布模型，通过仿真实验，证明了该算法的有效性和稳定性。

[1] 戚玉涛, 刘芳, 刘静乐, 任元, 焦李成. 基于免疫算法和EDA的混合多目标优化算法[J]. 软件学报, 2013, 24(10):2251-2266.

[2] 梁玉洁, 许峰. 自适应混合多目标分布估计进化算法[J].计算机工程与应用, 2014, 50(5): 46-50, 207.

[3] 周树德, 孙增圻. 分布估计算法综述[J]. 自动化学报,2007, 33(2): 113-124.

[4] Muhliebe H, Paass G. From recombination of genes to the estimation of distributionsI. binary parameters[C]. Lecture notes in computer science. Berlin, Germany: Springer Verlag,1996, 1141: 178-187.

[5] Pelikan M, Godberg D E, paz E C. Linkage problem, distribution estimation, and Bayesian networks[J]. Evolutionary Computation. 2000, 8(3): 311-340.

[6] Paul T K, Iba H. Linear and combinatorial optimizations by estimation of distribution algorithms[C]. 9th MPS Symposium on Evolutionary Computation, IPSJ, Japan, 2002.

[7] Qi Yu-tao, Liu Fang, Liu Ji-le, Ren Yuan, Jiao Li-cheng.Hybrid immune algorithm with EDA for multi-objective optimization[J]. Journal of Software, 2013, 24(10): 2251- 2266.

[8] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[9] ZHANG Qingfu, ZHOU Aimin, JIN Yaochu． RM-MEDA: a regularity model-based multiobjective estimation of distribution algorithm[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 41-63.

Multi-objective Optimization Problem Solved by Estimation of Distribution Algorithm

GAO Shang, LIU Yong
(1. School of Computer Science and Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;2. Artificial Intelligence of Key Laboratory of Sichuan Province, Zigong 643000)

Some methods for solving multi-objective optimization problems are discussed. In order to improve the convergence and accuracy of multi-objective optimization algorithm, a multi-objective optimization algorithm based on distribution estimation is proposed. 3 typical test functions of pateto-optimal sets were given. Through the 4 test functions, compared with the Nondominated Sorting Genetic Algorithm (NSGA-II) and Regularity Model-based Mul-tiobjective estimation of distribution algorithm (RM-MEDA), the test results show that the algorithm has good convergence and distribution, and the effect is stable.

Multi-objective optimization; Estimation of distribution algorithm; Convergence

TP18

A

10.3969/j.issn.1003-6970.2017.12.005

本文著录格式：高尚，刘勇. 基于分布估计算法的多目标优化[J]. 软件，2017，38（12）：25-28

人工智能四川省重点实验室开放基金(2016RYJ03)

高尚(1972-)，男，安徽天长人，教授，博士，从事智能计算研究；刘勇(1981-)，男，四川自贡人，实验师，硕士，研究方向为复杂系统优化。