基于Laplace-Adomian-Pade方法的超混沌系统分析

李 强，梁 秋

（1.四川三河职业学院基础部，四川 泸州 646000；2.四川省汶川中学，四川 汶川 624000）

基于Laplace-Adomian-Pade方法的超混沌系统分析

李 强1，梁 秋2

（1.四川三河职业学院基础部，四川 泸州 646000；2.四川省汶川中学，四川 汶川 624000）

利用Laplace-Adomian-Pade方法，对一个新构造的超混沌系统进行了数值求解，求得了系统的高精度近似级数解.结合M atlab软件进行数值仿真，得到了系统的时间序列轨迹图和混沌吸引子相图.最后对序列图和相图进行了分析，当初始值[x（t0）,y（t0）,z（t0）,w（t0）]=[1,1,1,1]，参数[a,b,c]=[-10,-4,-5]时，系统为混沌系统.研究结果表明，该法是分析超混沌系统的一种行之有效方法.

Laplace-Adomian-Pade方法；动力系统；混沌

自1975年李天岩和York首次提出混沌的数学定义以来，混沌理论及其应用已成为非线性科学领域中的一个热门课题．一些学者在Lorenz系统的基础上构造了许多诸如Chen系统[1]、T系统[2]、Bao系统[3]等变形系统，并对它们的复杂动力学行为、控制和同步方法进行了深入研究.这不仅加深了对混沌本质的认识，同时也促进了混沌理论的发展.基于混沌理论在保密通讯、图像加密、信号处理等领域的应用优势[4]，本文对一个新构造的四维超混沌系统进行了研究，利用Tsai和Chen提出的Laplace-Adomian-Pade方法[5]（LAPM）对系统进行了求解，求得了系统的高精度近似级数解.结合Matlab软件进行数值仿真，得到了系统的时间序列轨迹图和混沌吸引子相图.分析结果说明LAPM是分析混沌系统的一种有效方法.

1 Laplace-Adomian-Pade方法

Tsai和Chen在研究非线性Riccati方程时，提出了Laplace-Adomian-Pade方法（LAPM）用于求解非线性微分方程的初值问题，其基本思想是

对于给定的非线性微分方程

非线性项N[u(t)]用Adomian级数[6]替换并作Laplace逆变换得

2 超混沌系统的数值仿真分析

此时系统解的迭代形式为

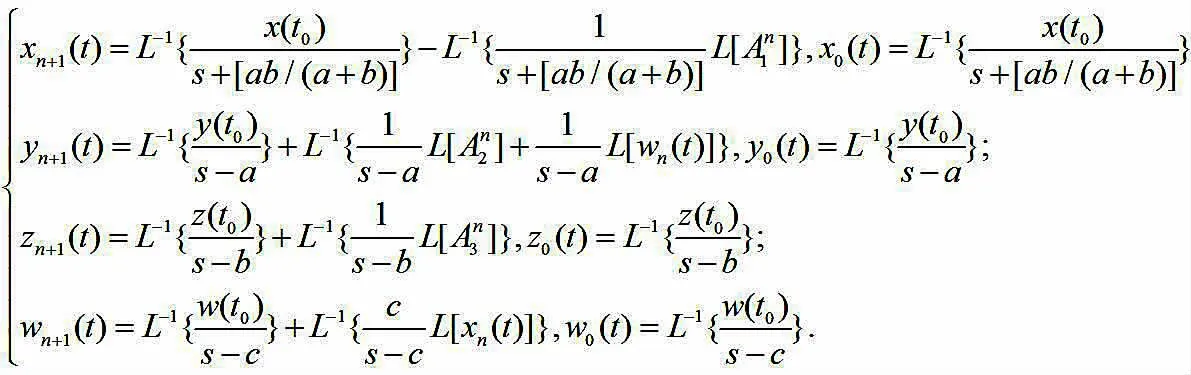
当初值[x（t0）,y（t0）,z（t0）,w（t0）]=[1,1,1,1]，系统参数[a,b,c]=[-10,-4,-5]，系统的 3 阶近似解为

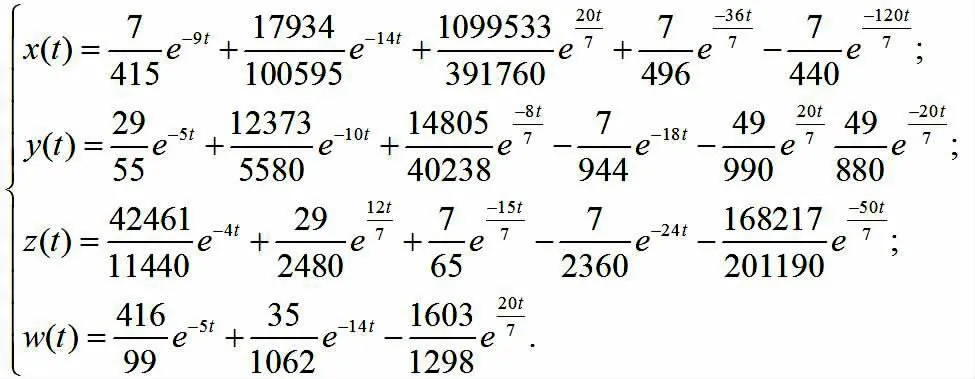
利用Pade逼近，则系统的3阶高精度级数解为

最后对系统进行仿真分析，得系统的时间序列轨迹图如图1-4所示，混沌吸引子相图如图5-8所示：

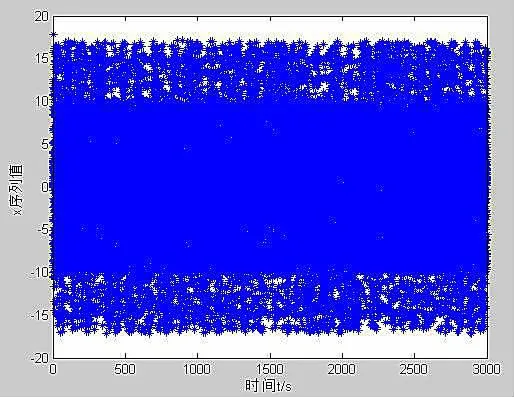
图1 系统x的时间序列图

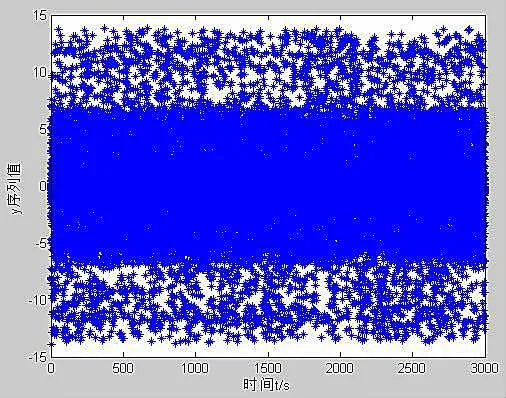
图2 系统y的时间序列图

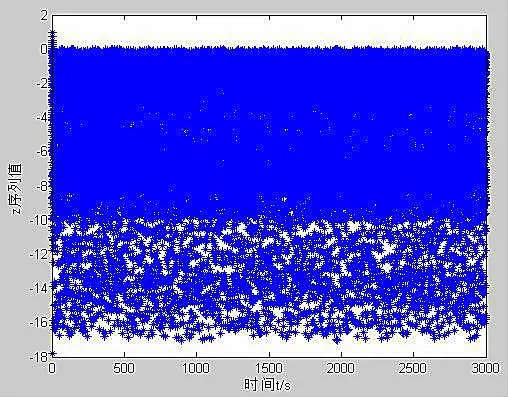
图3 系统z的时间序列图

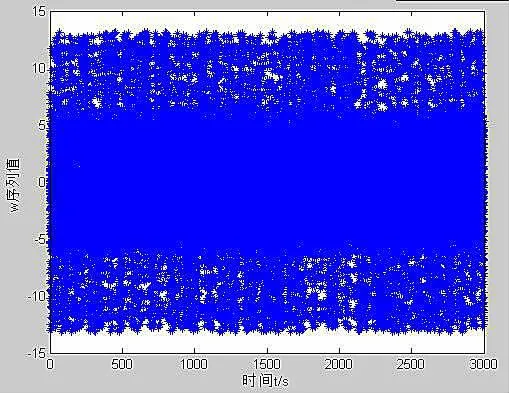
图4 系统w的时间序列图

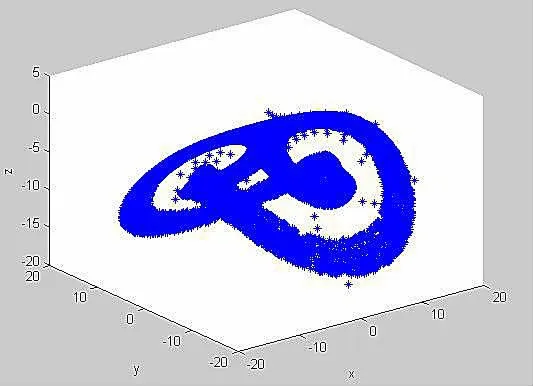
图5 系统x-y-z相图

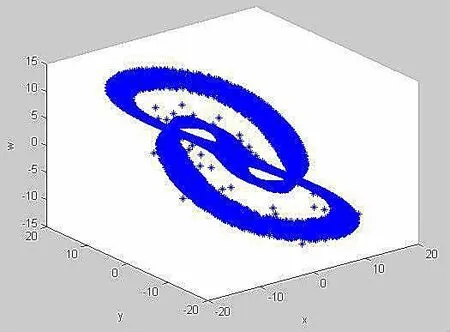
图6 系统x-y-w相图

图7 系统x-z-w 相图

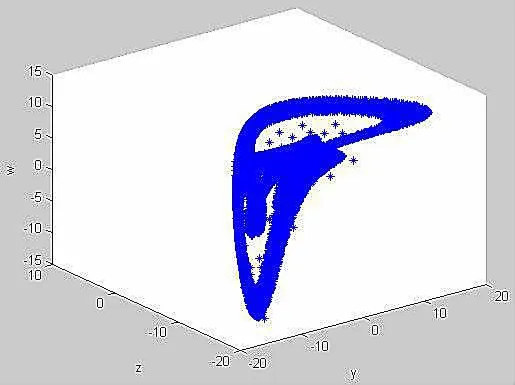
图8 系统y-z-w相图

由图1-4可知，当初始条件发生微小变化时系统表现出无序的混乱现象.图5-8中系统的混沌吸引子具有分形的结构和自相似性，说明此时系统处于混沌状态，为混沌系统.

3 结论

应用LAPM方法研究了一个新构造的四维超混沌系统，求得了系统的高精度近似解.利用Matlab软件对系统进行了仿真，得到了系统的混沌吸引子相图，分析了该系统的混沌行为，说明了该法的有效性，这为超混沌系统的理论研究和应用提供了理论支撑和参考.

[1]Chen Guanrong,Tetsushi UETA.Yet Another Chaotic Attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466.

[2]TIGANGH.Analysis of a Dynamical System Derived from the Lorenz System[J].Sci Bull Poli-tehnica University of Timisoara,2005, 50(64):61-70.

[3]Bao Bocheng,Liu Zhang,Xu Jianping.New Chaotic System and Its Hyperchaos Generation[J].Journal of Systems Engineering and Electrics, 2009,20(6):1179-1187.

[4]姚洪兴，张学兵，耿霞．Rucklidge系统的同步及其在保密通讯中的应用[J]．江苏大学学报，2006，72(2)：185-187．

[5]Tsai,Paiyee,Chen Chaokuang.An approximate analytic solution of the nonlinear Riccati differential equation[J].Journal of the Franklin Institute,2010,347(10):1850-1862.

[6]G Adomian,”Solving frontier problems of physics the decomposition method”,Springer,Ger-many,1994.

[7]刘春凤，张滑．DTM-Adomian-pade求解非线性分数阶微分方程[J]．西北大学学报（自然科学版），2016，46(3)：329-334．

[8]章秀君，吴志强，方正．超混沌系统的构造方法研究[J].计算机工程与应用，2014，50(2)：92-98．

Analysis of Superchaotic Systems Based on Laplace-Adomian-Pade

LI Qiang1,LIANG Qiu2
(1.Department of Basic Courses, Sichuan Sanhe College of Professionals, Luzhou Sichuan, 646000; 2.Wenchuan Middle School, Wenchuan Sichuan,624000)

We did the numerical solution to a new constructed superchaotic systems and obtained the system’s approximate series solution of high precision by Laplace-Adomian-Pade. Then, combined with Matlab,the numerical simulation was done to get the system’s time series trajectory map and chaotic attractor diagram.Finally,we analyzed the sequence map and diagram.When the initial value is[x（t0）,y（t0）,z（t0）,w（t0）]=[1,1,1,1],and the system parameter is[a,b,c]=[-10,-4,-5],it has become chaotic systems.The research result is that it is an effective method to analyze superchaotic systems

Laplace-Adomian-Pade;Power System;Chaos

张隆辉

O 145.5

A

1672-2094（2017）05-0162-05

2017-05-16

四川三河职业学院校级科研项目（编号：15XB0223）

李 强（1992-），男，四川达州人，四川三河职业学院专任数学教师.研究方向：分数阶微分方程及其应用.