基于磁光调制的光弹性应力快速测量方法

马剑涛，吴泳波，2，3，许伟鑫,刘楚彦,林 立,林跃裕,唐志列,2,3

(1.华南师范大学 物理与电信工程学院，广东 广州 510006;2.广东省光电检测仪器工程技术研究中心，广东 广州 510006;3.广东省量子调控工程与材料重点实验室，广东 广州 510006)

基于磁光调制的光弹性应力快速测量方法

马剑涛1，吴泳波1，2，3，许伟鑫1,刘楚彦1,林 立1,林跃裕1,唐志列1,2,3

(1.华南师范大学 物理与电信工程学院，广东 广州 510006;2.广东省光电检测仪器工程技术研究中心，广东 广州 510006;3.广东省量子调控工程与材料重点实验室，广东 广州 510006)

提出了基于磁光调制测量光弹性应力的方法，并设计了包括终端配套软件在内的一体化测量装置. 通过贝塞尔函数展开推导应力大小及方向的公式，实验中仅需旋转起偏器一次来确定应力的实际方向，降低了旋转玻璃样品在装置设计上的难度；并利用磁光调制的方式正弦调制入射激光，通过检测光强频谱图精准判断消光位置，保证测量的精准度. 实验结果表明，通过此方法测得的应力大小及方向精度高，完成一组测量的速度较快. 多组测量数据的离散度较小，约1 nm/cm，运用该方法对有应力分布的平板玻璃和受压玻璃进行测量并扫描成像，得到它们的应力分布图像. 该方法能够准确、快速和无损地测量光弹性样品任意位置的应力.

光弹性应力;磁旋光;应力测量;磁光调制;应力分布

光弹技术是基于透明材料双折射现象的一种测量、检测技术，在异性纤维检测[1]、透明材料显色研究[2-3]、地震场分析[4]、生物医学成像[5]等领域有重要应用. 光弹分析中相位信息的处理被广泛应用于玻璃应力双折射的测量中，主要有移相法[6-8]、补偿器技术[9]、斯托克斯参量法[10-11]、调制法[12-14]等. 移相法分析移相应力条纹图实现延迟量测量，对图像处理技术有较高要求；补偿器技术利用光程差可调元件平衡延迟量对应力双折射进行测量；斯托克斯参量法通过调节偏振片和1/4波片确定斯托克斯量，并提出分振幅多光路测量的思想改进方案[11]. 而调制法对探测激光进行调制，通过输出光强的谐波分析精准判断双折射延迟量，基于光弹调制器(PEM)的实现已取得不错进展，近年来磁光调制器的提出为应力测量提供更多的设计思路.

相比于光弹调制器的复杂性及高昂造价，磁光调制法展现了广阔的应用前景. 运用磁光玻璃制成调制器，正弦调制入射激光，分析输出光强的变化精准判断检偏器消光点，从而确定应力方向及大小. 传统磁光调制法[14]需旋转玻璃360°多组测量确定应力方向，工程繁琐. 李春艳[15]引入旋光器简化测量步骤，但由于旋光器对磁光玻璃维尔德系数要求较高且大电流导致线圈发热会引起误差，不利于大数值应力的测量. 为此本文提出一种改进的磁光调制法测量光弹性应力，在不使用旋光器的基础上，根据第一类贝塞尔函数展开输出光强公式，仅需改变1次玻璃方向即可完成测量，无需旋光器即可对测量方法进行简化，并提出旋转起偏器代替旋转待测玻璃，避免了旋转装置的设计，在简化实验装置的同时实现了玻璃应力的快速、大范围测量.

1 实验原理

基于玻璃的光弹性效应[16]，利用检偏器测量光束经过待测玻璃产生的相位差，通过磁光调制的方法可以提高检偏器消光点判断的准确度.

1.1 测量原理图

如图1所示，激光器发出的椭圆偏振光经透镜和起偏器后变成线偏振光，并入射到磁光调制器中进行调制. 经正弦调制的偏振光通过玻璃后偏振方向会产生一定变化，再经过检偏器和透镜射出，由光电探测器接收光强值并利用计算机软件输出光强波形图与傅里叶频谱图.

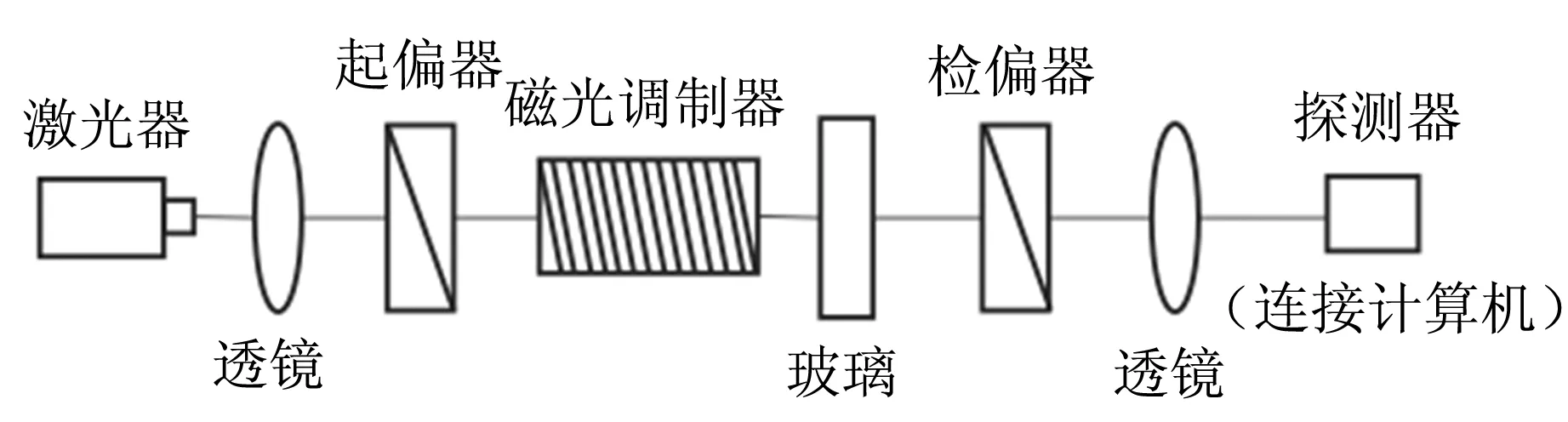
图1 实验测量装置示意图

采用paulone ZY0022型激光器，波长650 nm，功率5 mW. 探测器由光照传感器BH1750FYI模块组成. 调制器由磁光玻璃外加绕制约1 200匝线圈组成，磁光玻璃采用维尔德系数约为800 V/(°)·T-1·m-1的重火石玻璃，对线圈通以适当的交流电压产生正弦变化磁场，以保证有足够的调制幅度.

图2所示为各光学元件的光轴方位及夹角，以起偏器的透振方向作为参考方向x轴，易得起偏器的琼斯矩阵为

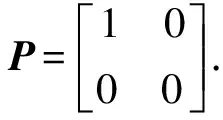
(1)

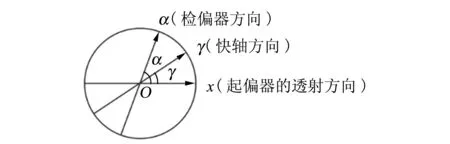
图2 光学器件光轴方向示意图

设检偏器光轴与起偏器光轴的夹角为α，则其琼斯矩阵为

(2)

设样品应力方向(快轴方向)相对起偏器光轴的夹角为γ，且其双折射相位差为δ，则琼斯矩阵表示为

(3)

磁光调制器的调制角度θ=θ0sinωt，θ0为调制角幅度，ω为调制频率，琼斯矩阵表达式为

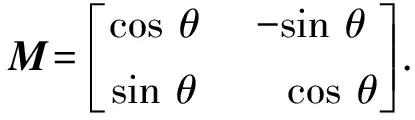
(4)

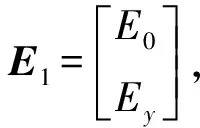
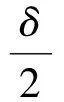
(5)

1.2 光强检测和样品双折射大小的测量

1)出射光出射后进入光电探测器后，探测器探测到的光强Iout为

Iout=|E2|2=

(6)

2)将输出光强式(6)用第一类贝塞尔函数展开[14]，输出光强分为直流、基频和倍频3部分,即

2AJ2(2θ0)cos 2ωt,

(7)

其中，根据第一类贝塞尔函数定义：

(8)

(9)

(10)

3)考虑消光位置的输出光强特点,在消光位置根据对称性，磁光调制器加正反等值电压时输出光强相等，即Iout(θ)=Iout(-θ)，代入式(6)得

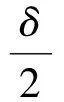
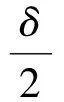
(11)

整理得，

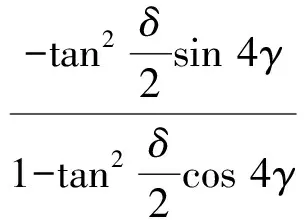
(12)

将式(12)代入式(10)得B=0，即消光时输出光强基频信号幅值为零.

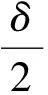
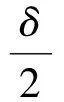
(13)

式(13)表明应力双折射相位差只与应力方向γ和检偏器读数α有关，则通过获得2个不同应力方向下消光位置的检偏器读数，代入式(13)联立方程即可推得应力双折射方向和大小的表达式.

设第一次测量时检偏器读数α1，应力方向γ1，则

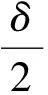
(14)

旋转起偏器Δ( 改变样品应力的相对方向)，此时γ2=γ1+Δ，再次旋转检偏器至消光位置，此时检偏器在原参考方向下的读数α2=α′-Δ，(α′为检偏器的读数)，则

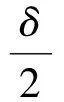
(15)

联立(14)和(15)两式，两式右边相等，可以解得：

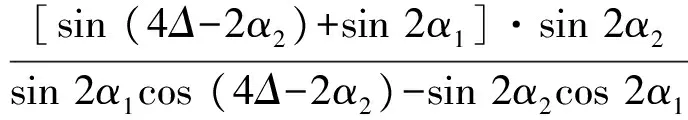
(16)

则可以解得内应力的方向γ1为

(17)

将式(17)代入式(14)，则应力双折射相位差为

(18)

则应力双折射大小δn为

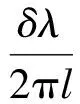
(19)

式中l为待测玻璃样品的厚度.

2 实验结果与讨论

2.1 检偏器消光位置的波形图判断

为保证偏振光有足够的调制幅度且调制频率满足传感器的数据采样率，本文采取调制频率为6 Hz.

将所接收的数据进行数字信号平滑、滤波与傅里叶逼近拟合得到光强输出的波形图，再利用快速傅里叶变换(FFT)输出光强的频谱图. 在消光位置，基频信号为零，输出光强为仅含倍频的标准正弦信号，如图3(a)所示. 在消光点附近，输出波形近似为标准正弦波，需根据傅里叶频谱分析进一步确定消光. 如图3(b)所示，不考虑噪音信号的影响，频谱图中仅含倍频信号，基频信号峰值为零.

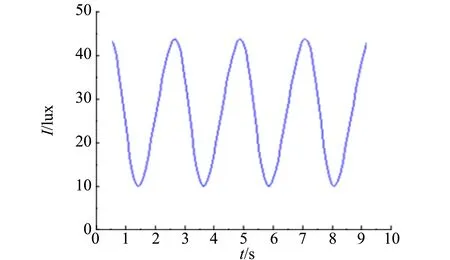
(a)消光位置光强波形图

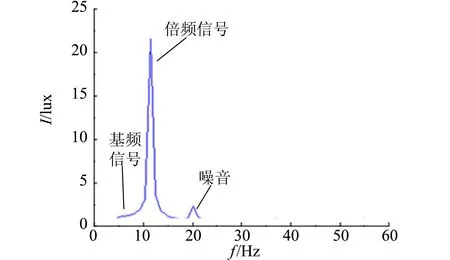
(b)消光位置傅里叶频谱图图3 消光位置光强波形图和消光位置傅里叶频谱图

2.2 玻璃样品单点应力测量

激光的波长为650 nm，待测玻璃的厚度为14.980 mm，对玻璃中心点应力进行测量. 从0～50°，每次旋转起偏器10°，重复实验测得数据，每相邻2组数据可测得1次玻璃应力大小与方向，计算结果如表1所示.

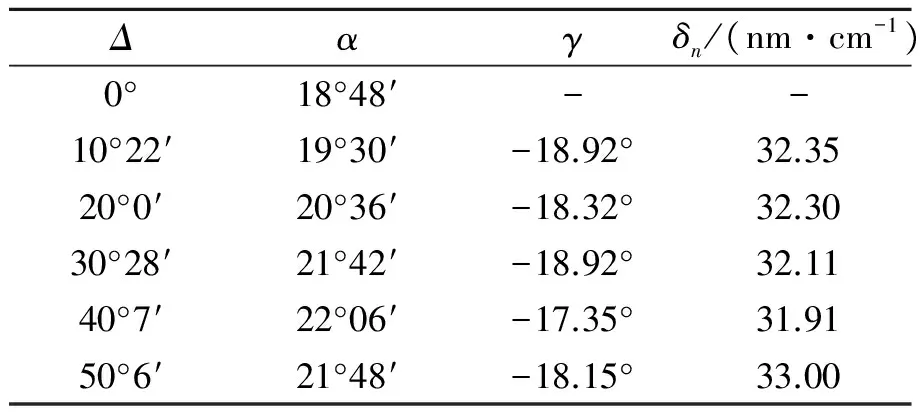
表1 玻璃中心点测量记录(初始参考系下)

测量结果δn=(32.3±0.5) nm/cm，Er=1.5%.γ1=-18.2°±0.7°，Er=3.8%. 中心点应力测量的各组数据的离散度很小，约1 nm/cm，测量的准确率高.

2.3 玻璃样品大小热区分布

玻璃夹持装置可将样品沿水平、竖直方向二维移动，使激光入射玻璃上不同点，扫描式测量玻璃上不同点应力的大小值，扫描范围为9.0 cm×0.9 cm，扫描间隔为5 mm，用Matlab插值拟合测得的应力大小，得热区分布如图4所示.

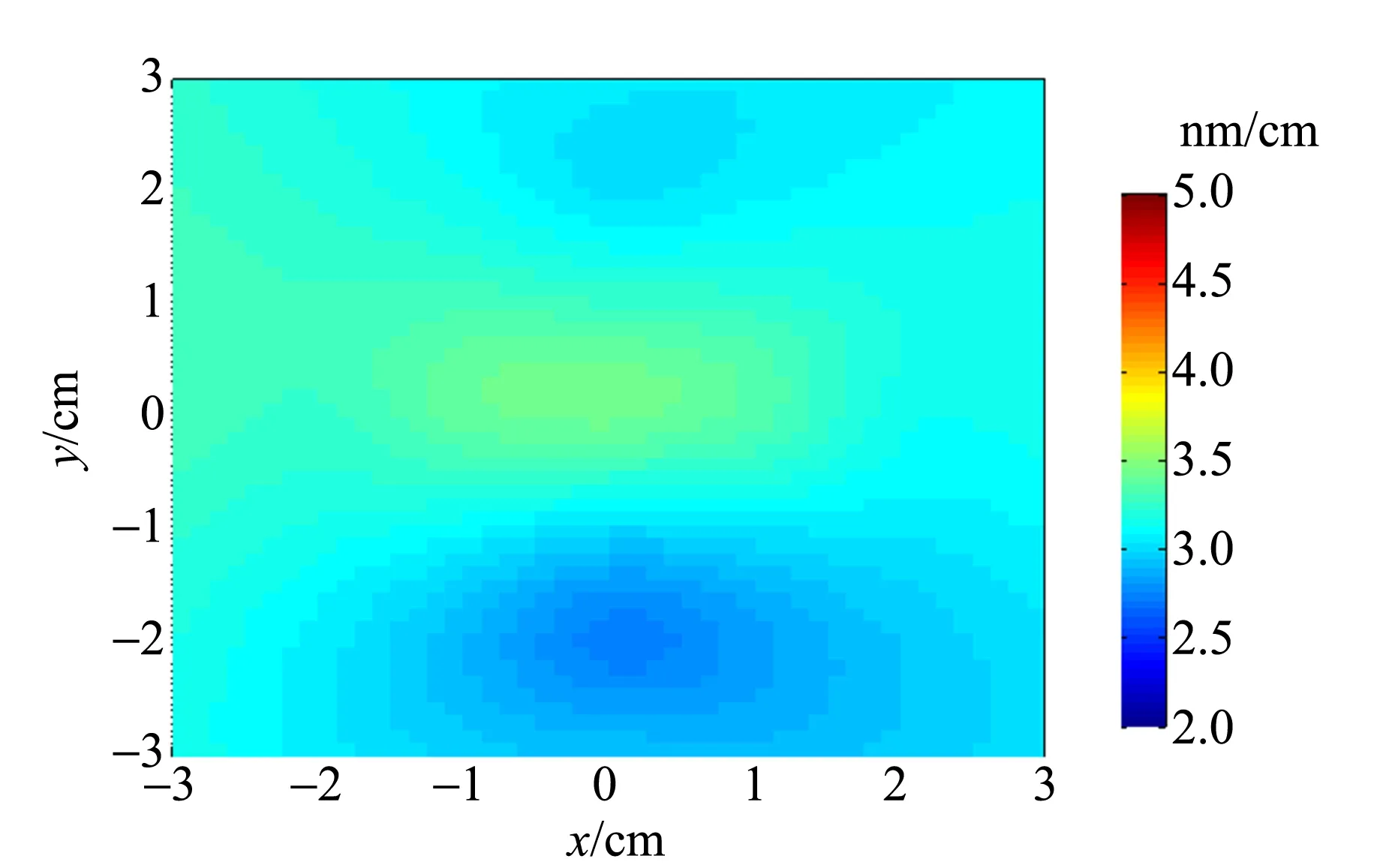
图4 玻璃应力大小热区分布二维显示

热区图通过颜色显示玻璃的应力大小，颜色越接近红色说明应力值越大，反之越接近蓝色则应力值越小.
图4可以看出玻璃样品应力大小无集中分布，说明此玻璃不易发生断裂，质量较好.

2.4 外应力的影响验证

外力将改变玻璃内部结构，导致应力分布变化，体现在应力双折射大小的变化. 运用压力夹给玻璃上方施加一定压力，测量应力及其分布.

测得此时的中心点应力δn=(42.6±0.6) nm/cm，Er=1.4%. 通过扫描光点测量的方式，得到应力大小热区分布如图5所示.

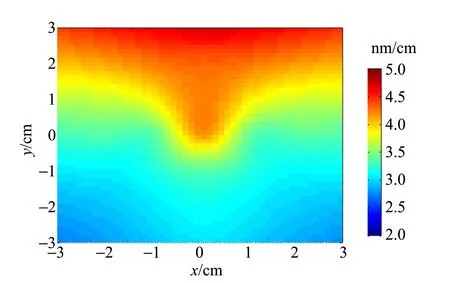
图5 外力下玻璃应力大小热区分布二维显示

分析上述结果，给玻璃施加外力后，顶部的应力大小增加，证明装置测量的数值的确为玻璃样品的应力. 热区图显示样品在外加压力后的应力分布，图5顶部出现明显的应力集中，对应所加压力位置，进一步验证实验装置的可靠性.

3 结束语

本文提出了基于磁光调制的光弹性应力高精度、快速测量方法，改进了计算公式与测量方法，避免已有方法在旋转玻璃样品设计上的困难，装置具有更高的适用性. 通过傅里叶频谱图精准判断消光位置，提高装置测量的精度，并配套终端软件进行显示与计算，实现装置的一体化设计. 实验结果表明，此方法测量离散度小，完成单次测量仅需旋转起偏器1次以确定实际应力方向，并通过验证实验的设计保证结果的可靠性. 本文提出的方法在简化实验流程的同时保证结果的准确度，实验装置设计更加紧凑，提高了磁光调制方法测量光弹性应力的适用性.

[1] 张华林. 光的弹性效应在异性纤维检测中的运用[J]. 科技创新与应用, 2016(27):77.

[2] 郑智武,陈孔韬,郭建波,等. 对液晶受压产生变色现象的探究[J]. 物理实验, 2015,35(7):1-5.

[3] 袁晓庆,陈靖丰,刘丽飒. 透明塑料盒上的显色偏振[J]. 物理实验, 2015,35(4):42-46.

[4] 黄兴,胡宏玖,王华林,等. 沂沭断裂带构造区光弹实验与地震危险区判定研究[J]. 中国地震,2015,31(3):529-543.

[5] Montalto L, Rinaldi D, Scalise L, et al. Photoelastic sphenoscopic analysis of crystals [J]. Review of Scientific Instruments, 2016, 87(1):40-48.

[6] 张丽君,沙定国,聂林秋. 基于移相法的光学玻璃应力等倾角全场数字化测量[J]. 光学技术,2004,30(2):000199-203.

[8] 李金鹏, 陈磊, 乌兰图雅,等. 基于移相算法的玻璃应力延迟量快速测量方法[J]. 光学学报,2013,(6):117-121.

[9] Hutsel M R, Ingle R, Gaylord T K. Accurate cross-sectional stress profiling of optical fibers [J]. Applied Optics, 2009,48(26):4985-4995.

[10] Kihara T. An arctangent unwrapping technique of photoelasticity using linearly polarized light at three wavelengths [J]. Strain, 2003, 39(39):65-71.

[11] 李志诚,唐志列,陈萍,等. 基于斯托克斯参量的光弹性应力分布及成像方法研究[J]. 光学学报, 2012,32(5):93-97.

[12] 胡建明,曾爱军,王向朝. 基于光弹调制技术的波片相位延迟量测量方法[J]. 光学学报, 2006,26(11):1681-1686.

[13] 吴易明,高立民,李明,等. 一种玻璃材料内应力精密测定的方法[J]. 光子学报, 2010,39(3):490-493.

[14] 李春艳,吴易明,高立民,等. 磁光调制法测量玻璃内应力[J]. 光学 精密工程,2014,22(1):58-62.

[15] 曹绍谦,步扬,王向朝,等. 基于单光弹调制器的米勒矩阵测量方法[C]// 全国光学测试学术讨论会. 2012.

[16] 姚启钧. 光学教程[M]. 5版. 北京.高等教育出版社,2008:249-250.

Fastmeasurementofphotoelasticstressbasedonmagneto-opticalmodulation

MA Jian-tao1, WU Yong-bo1,2,3, XU Wei-xin1, LIU Chu-yan1,LIN Li1, LIN Yue-yu1, TANG Zhi-lie1,2,3

(1.School of physics and Telecommunication Engineering，South China Normal University, Guangzhou 510006, China;2.Guangdong Research Center of Photoelectric Detection Instrument Engineering Technology, Guangzhou 510006, China;3.Guangdong Laboratory of Quantum Engineering and Quantum Materials,Guangzhou 510006, China)

A new method for measuring the photoelastic stress using magneto-optical modulation was proposed, and an integrated measuring device was designed including the terminal supporting software. The formulas of stress magnitude and direction were deduced by Bessel expansion. The real direction of the stress was determined by rotating the polarizer only once, which reduced the difficulty in designing rotation device for glass sample. In addition, the incident laser was sinusoidally modulated by magneto-optical modulation, the extinction position was accurately determined through light intensity spectrum, and the accuracy of the measurement was ensured. The experimental results shown that the measurement of stress magnitude and direction by this method had high precision, and the speed of measurement was fast. The accuracy of the experimental setup was further illustrated by confirmatory experiments. A glass plate with internal stress and a glass sample subjected to compressive load, were scanned with this method separately, and their stress distribution were obtained. This method could measure the stress at any position in the photoelastic sample accurately, rapidly and nondestructively.

photoelastic stress; magnetic rotation; stress measurement; magneto-optical modulation; stress distribution

2017-06-06

国家自然科学基金资助(No.61575067)

马剑涛(1996-)，男，广东汕头人，华南师范大学物理与电信工程学院2014级本科生.

指导教师：吴泳波(1984-)，男，广东揭阳人，华南师范大学物理与电信工程学院实验师，硕士，主要从事光电检测技术、光声共焦显微成像技术等方面的研究.

O348.1

A

1005-4642(2017)12-0045-05

郭 伟]