探究立几最值 提高数学素养

河南省平顶山市第一中学 张玲敏

河南省平顶山市第一高级中学 刘海洋

探究立几最值 提高数学素养

河南省平顶山市第一中学 张玲敏

河南省平顶山市第一高级中学 刘海洋

求解立体几何的最值问题,要么构建目标函数,要么利用几何性质,探究两种途径在发生和发展过程中所蕴含的思维方法,可以提高构建函数模型、直观想象、逻辑推理、合理运算等核心素养,凸显空间问题“平几化、代数化、特殊化、逻辑化”的本质属性。

一、构建目标函数模型求解立几最值

1.依据正三棱锥的特征构建函数模型,导数法求解包装问题中的最值。

例1 某商场为促销要准备一些正三棱锥形状的装饰品,用半径为1 0c m的圆形包装纸包装。要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图1所示。设正三棱锥的底面边长为xc m,体积为Vc m3。在所有能用这种包装纸包装的正三棱锥装饰品中,V的最大值是多少?并求此时x的值。

图1

解析:正三棱锥侧面开展铺平内接于半径为1 0c m的圆内。按照底边包装时体积最大,设正三棱锥侧面的高为h0,高为h。

当x∈(0,8 3)时,y′＞0,当x∈(8 3,1 0)时＜0,所以当x=8时,y取得最大值,即ymax=1 53 6 0,Vmax=3 2(c m3)。

素养点击:借助半径为1 0c m的圆形包装纸包装正三棱锥,利用斜高和底面边长x+h

0=1 0的关系,构建三棱锥体积和边长的函数模型,导数法求最值解决了包装的实际应用问题。

2.利用圆锥的几何特征构建目标函数,通过均值不等式求体积的最值。

图2

例2 某工件的三视图如图2所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用

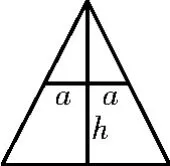
图3

解析:作出轴截面,如图3,设长方体的长,宽,高分别为x,y,h,长方体的上底面与圆锥的截面半径为a,所以x2+y2=4a2=,所以h=2-2a,所以V=x y h≤h=2a2h=(2 -2a)=

素养点击:借助圆锥的轴截面探究内接长方体的长、宽、高与圆锥的截面半径的关系,合理选择圆锥的截面半径为变量构建函数模型,利用三元基本不等式求其最值,进而解决了新定义的材料利用率问题。

二、几何法探求立几最值

1.利用垂直关系确定高的最值。

例3 (2 0 1 7年云南省部分名校高三1月)表面积为6 0 π的球面上有四点S、A、B、C,且△A B C是等边三角形,球心O到平面A B C的距离为3,若平面S A B⊥平面A B C,则三棱锥S-A B C体积的最大值为____。

解析:由题意画出几何体的图形,如图4,因为球的表面积为6 0 π,所以球半径为,由于面S A B⊥面A B C,所以点S在平面A B C上的射影D落在A B上。设O在平面A B C上的射影为O′,由于O O′⊥平面A B C,S D⊥平面A B C,即有O O′∥S D,当D为A B的中点时,S D最大,三棱锥S-A B C的体积最大。由于O C=,O O′=,则 C O′=,D O′=,故△A B C是边长为6的正三角形,S△ABC=×62=9 3。在直角梯形S D O′O中,作O E⊥S D于点E,O E=D O′=,D E=O O′=3,S D=D E+S E=+=3 3,即有VS-ABC=S h=×9×3=2 7。

图4

素养点击:求底面为定值的三棱锥的体积的最值,可以合理转化为求高的最大值,借助面面垂直性质和球的属性再转化为平面内直角梯形S D O′O下底的长,整个转化探究过程可以提高同学们的直观想象、逻辑推理、合理运算等核心素养。

2.依据正方体和正四面体的特征确定最值。

例4 一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )。

A.2 B.3 C.1 D.2

解析:正四面体内放一个正方体,可以任意转动,则这个正方体就是这个正四面体的内切球的内接正方体。容易求得,棱长为6的正四面体的内切球半径为×6=,于是这个球的内接正方体的体对角线长为6,设正方体的棱长为x,则3x=6,于是x=,即满足条件的正方体棱长的最大值为,选择D。

素养点击:正四面体的内接最大正方体,都是多面体,无法直接寻找关系,我们通过寻找球来过渡,在正四面体和正方体中依靠球来转换,先寻找正四面体的内切球半径,再求解这个球的内接正方体的棱长。借助空间认识事物的位置关系、形态变化与运动规律。

3.铺平法探究多面体或旋转体表面上两点间的距离。

图5

例5 如图5,已知圆锥的底面半径为1,母线A S长为6,M为A S的中点,有一根绳子从A点出发,沿圆锥的侧面绕一周到达M点,问绳子最短是____。

解析:如图5,沿母线S A将圆锥侧面展开,A,M点分别对应展开图中的A1,M1点,则在展开图中,线段AM1的长度即为最短绳长。因 为 ∠AS A==6 0°,

1S A1=S A,所以△S A1A是正三角形,所以AM1⊥S A1。所以 AM1===3,即绳子最短为3 3。

素养点击:多面体或旋转体表面上两点的最短距离,“沿母线或棱剪开铺平侧面展开化为平面上两点之间的距离”求解。

注:本文系河南省教育科学“十三五”规划2 0 1 7年度课题“高中数学核心素养的案例研究”(课题编号:【2 0 1 7】-J K G B-0 7 1 4)的阶段性研究成果之一。

(责任编辑 王福华)