基于MEMS加速度传感器的轴承故障检测*

张 毅

(长治学院电子信息与物理系,山西 长治 046011)

基于MEMS加速度传感器的轴承故障检测*

张 毅*

(长治学院电子信息与物理系,山西 长治 046011)

提出了一种通过利用低成本的MEMS加速度传感器进行振动分析,实现检测电动机深沟球轴承多重故障的简易方法。首先分析了轴承多故障特征频率,然后通过快速傅里叶变换算法对轴承出现故障的电动机振动频率进行了分析,从振动频谱中提取故障频率来诊断轴承多重故障的存在。同时,基频分量周围的边带频率分量表明由于故障轴承存在空气间隙。在空载、单相以及失衡电压条件下通过实验对提出的方法进行了研究,结果显示提取出的故障频率与理论值两者十分接近,表明提出的方法能够有效检测并识别出感应电动机的多故障特征。

快速傅里叶变换算法;MEMS加速度传感器;故障检测;振动特征分析

轴承是感应电动机的关键部件,对感应电动机安全可靠的运行发挥着重要作用。工业电动机的可靠性研究表明,大约50%的电动机故障主要是轴承故障。因此,从工业方面来看,有必要对轴承状态进行监测[1-2]。轴承出现故障的原因如下:污染、腐蚀、位置偏差、安装润滑不当以及意外受到电气应力、机械应力和环境应力[3-5]。另外,由于电源电压失衡,负序电流通过轴和轴承从定子流向转子。通过轴和轴承的负序电流会导致轴承的温度升高,从而使表面粗糙,即电气开槽[6]。轴承出现多故障会导致电动机出现动态间隙偏心率,进一步增大不平衡,因此会使得转子与定子产生摩擦[7]。

可以通过电流、振动、温度、声发射、冲击脉冲等监测量对传统轴承故障进行检测。文献[6-7]对内外圈轴承出现故障的电动机定子电流进行了分析。采用幅度调制技术检测内外圈轴承故障,并进行振动十分复杂分析,和数据处理需要花费较长时间来识别轴承故障。

文献[8]等利用传统压电加速计来捕获轴承故障振动信号。但此类加速计会导致晶体过热,反过来会削弱信号变换能力。为了解决此问题,需使用其他温度补偿电路。另外,也可以使用位移计来监测轴承状态,但是此类机械振动传感器成本较高、灵敏度也较高。因此,相较于中低马力电动机,更适合监测临界、高马力电动机[9]。

可以通过快速傅里叶变换以及小波技术对电动机振动信号进行处理。文献[10]将定子电流作为媒介,采用小波和状态向量机方法检测内外圈缺陷,但是其计算过程十分复杂,且小波方法所需计算机内存较大,处理时间较长,并且需要技术人员进行故障分析。因此,从工业角度来看,在线故障诊断十分困难。

以往文献大多数研究内外圈的单点缺陷、双点缺陷、一般表面粗糙度以及组合故障,但并未研究通过振动分析进行滚动轴承多故障检测的问题。现实情况中,皮带驱动电动器常会出现此类故障。因此,本文提出利用低成本的MEMS加速计进行振动分析,通过快速傅里叶变换算法对轴承出现故障的电动机振动频率进行频谱变换,从振动频谱中提取故障频率来检测并诊断感应电动机轴承多故障。

1 轴承故障特征频率

图1是本文采用的NACHI 6205 ZE轴承的几何结构。表1是轴承的详细规格参数。

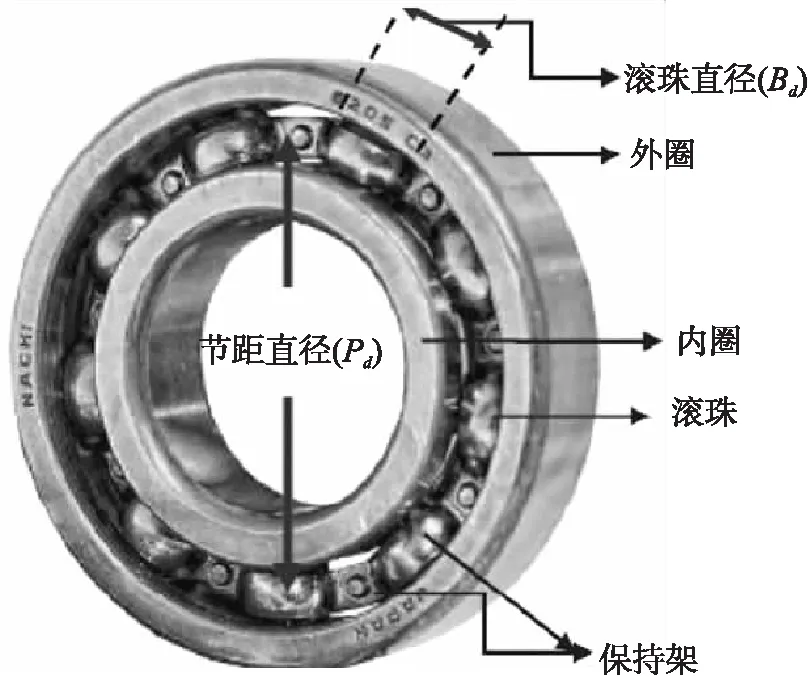
图1 本文所用深沟球轴承的几何结构

材料内径/mm外径/mm轴承宽度/mm滚珠直径Bd节距直径Pd最大转速/(rad/min)数值2552157.9439.416000

不论轴承出现何种故障,都会扩大机械振动。每类轴承的振动特征频率均独一无二,如文献[10]所示。轴承内圈故障频率(BPFI)可以表示为:

(1)

轴承外圈故障频率(BPFO)可以表示为:

(2)

轴承滚动件损坏频率(BSF)可以表示为:

(3)

保持架缺陷频率或者轴承保持架损坏频率(FTF)可以表示为:

(4)

式中:nb为滚珠数量,N为转速(rad/min),fr=N/60表示机械转子频率(Hz),P表示一对极点,Bd为滚珠直径(mm),Pd表示轴承节距直径(mm),α表示滚珠与座圈的接触角度。

2 轴承多重故障的数学分析

通过单位脉冲序列卷积可获取轴承多故障的振动信号特征值,脉冲序列由缺陷点生成。轴承故障会导致空气间隙不均匀性,进而引起电动机振动。因此,轴承出现多故障的电动机总振动可表示为:

v(t)=hM(t)hd(t)+g(θ,t)

(5)

式中:v(t)表示电动机产生的振动。hd(t)表示缺陷生成的脉冲序列,T为其周期。Ts为带通滤波器脉冲周期可表示为:

(6)

hM(t)表示机器的脉冲响应,可表示为:

hm(t)=[ω(t)hMR(t)]e-ζt

(7)

式中:ω(t)表示包含随机振动信号的白噪声,hMR(t)表示与谐振频带对应的带通滤波器,最大振动信号强度在此频带中。e-ζt项表示故障导致的脉冲信号指数衰减,故障是由机器阻尼因数ζ生成。卷积项ω(t)·hMR(t)提供了每个脉冲诱发的振动,每个脉冲均由故障点生成。

g(θ,t)表示轴承缺陷导致的空气间隙,可表示为:

(8)

当外圈缺陷时ψ(t)=0;当内圈缺陷时ψ(t)=wrt;当滚珠缺陷时ψ(t)=wcaget。其中,g0为恒定间隙长度(mm);e=e0或ei或eb,表示t=k/f0、t=k/fi以及t=k/fball时外圈缺陷、内圈缺陷以及滚珠缺陷导致的相对偏心度;ωr为角频率;ωcage为基本保护架频率。

图2表示本文使用的多故障轴承。A-A′和B-B′点表示外圈和内圈的双点缺陷。C和D点表示保持架以及滚珠的单点。轴承上的数字1～9表示滚珠。假设内圈逆时针旋转,外圈固定。从图2可以看出,滚动体6首先会通过A′和B′的外圈缺陷和内圈缺陷,然后位于负载区的缺陷滚动体5以及剩下的滚动体会依次通过。

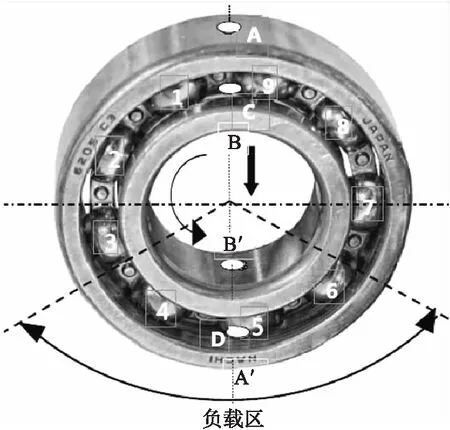
AA′为外圈、BB′为内圈、C为保持架、D为滚珠图2 本文使用的多故障深沟球轴承轴承

由于内圈旋转时有缺陷,传动轴的旋转轴不断变化;而外圈固定,所以旋转轴静止。因此,由于轴承出现多重故障,电动机会存在静态和动态偏心率,统称为混合间隙偏心率,因而出现振动。另外,当出现故障的轴承在负载区内运行时,径向负载会导致滚珠以及座圈出现更多应力。因此,当出现故障的轴承在非负载区内运行时,电动机的振动较弱。

因此,轴承出现多重故障导致出现轴承偏心率,此时电动机的总振动可表示为:

v多故障(t)=[v2,OR(t)+gOR(θ,t)×[v2,IR(t)+gIR(θ,t)×

[v1,ball(t)+gball(θ,t)×[v1,cage(t)+gcage(θ,t)

(9)

式中:gOR(θ,t)表示外圈缺陷导致的空气间隙,v2,OR为外圈的双点缺陷,可表示为:

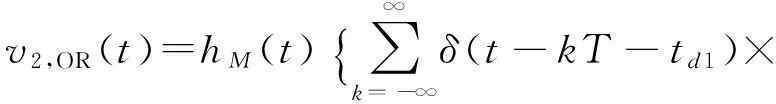
(10)

gIR(θ,t)为内圈缺陷导致的空气间隙,v2,IR为内圈的双点缺陷,可表示为:

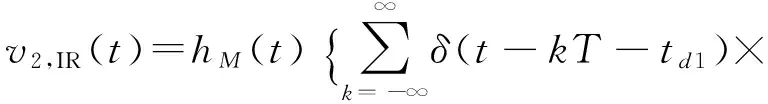
(11)

gball(θ,t)表示滚珠缺陷导致的空气间隙,v1,ball表示滚珠的单点缺陷,可表示为:

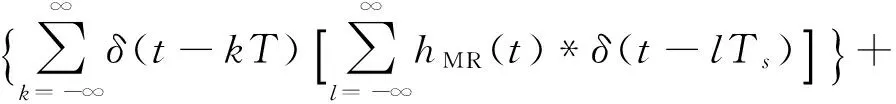
(12)

gcage(θ,t)=保持架缺陷导致的空气间隙,v1,cage=保持架的单点缺陷,可表示为:

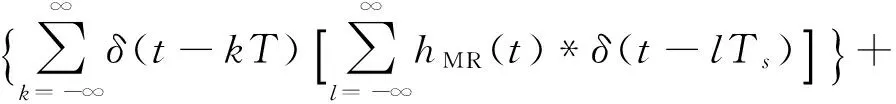
(13)

在式(10)和式(11)中,td1和td2表示不同缺陷生成的脉冲之间的延迟,如图2所示。轴承多故障导致的振动综合了子组件的单点缺陷和双点缺陷,在本质上十分复杂。

当轴承出现多重故障时,感应电动机在空载条件下运行,转子的径向运动会导致出现混合间隙偏心率。多点缺陷频率是单点缺陷频率的整数倍(式(1)～式(4))。利用MEMS加速计捕获电动机振动信号,并利用FFT分析仪进行频谱幅度观察,如果出现明显离散峰值,则其离散峰值分别为故障频率fcage、fo、fi和fball,表明保持架、内外圈以及滚珠存在故障,从而实现检测轴承多故障特征。

图3 实验设置

3 实验结果与分析

3.1 实验环境设置

图3是本文的实验环境设置,其中包括额定功率1.5 kW、电压415 V、频率50 Hz以及转速1 440 rad/min的三相感应电动机,并利用皮带进行机械装载。使用的仪器包括ADXL322JCP MEMS加速计、高分辨率FFT分析仪以及通过RS-232电缆与台式电脑,MEMS加速计安装在电动机上,实验安装连接框图如图4所示。

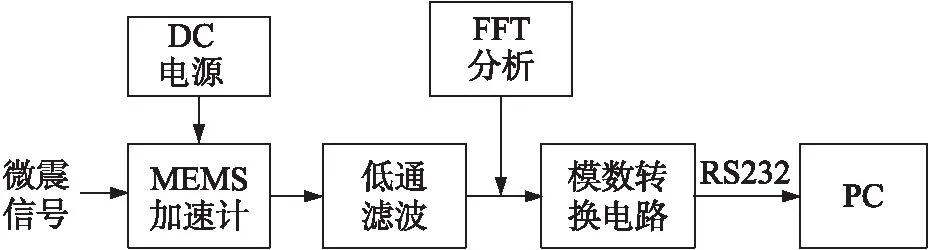
图4 基于MEMS加速计的系统连接框图

图4中MEMS加速计如图5所示,其原理框图如图6所示,Yout为Y轴通道输出,Xout为X轴模通道输出,ST为自检测引脚。从图3可以看出,本次实验中使用了2个NACHI 6205-ZE轴承,轴承1无故障,如图1所示;轴承2存在多重故障,由电火花线切割机人为切割产生,如图2所示。ADXL322JCP MEMS加速计的带宽范围为0.5Hz到2 500 Hz,可通过CX、CY进行调节,在本实验室中CX=CY=0.02 μF。

图5 本文使用的MEMS加速计

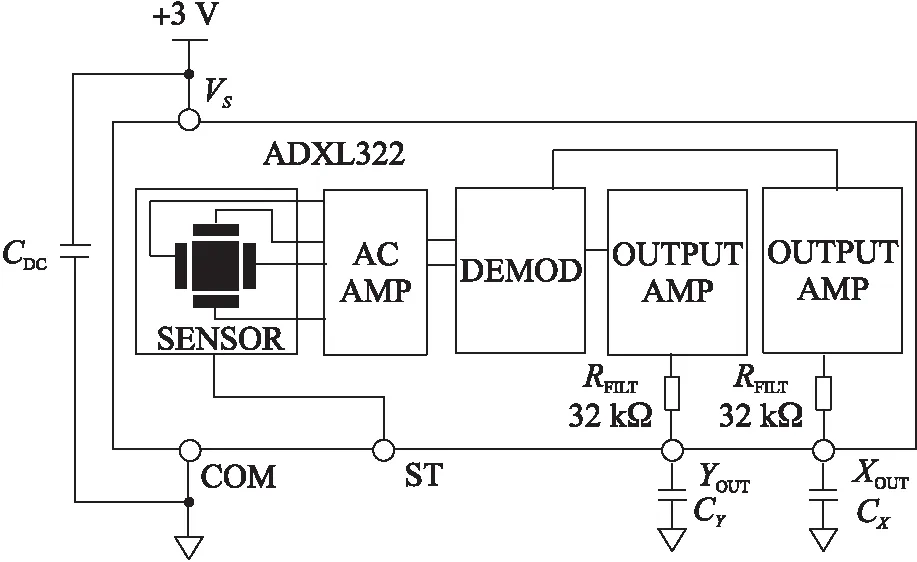
图6 ADXL322JCP原理框图

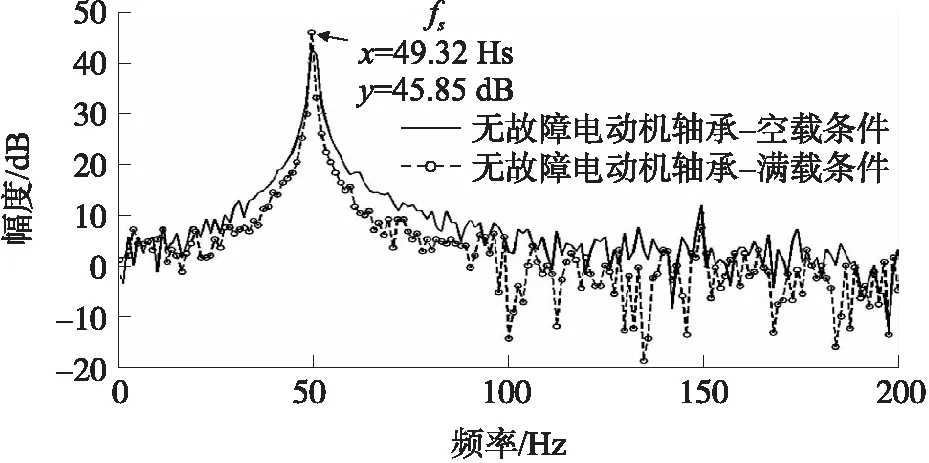
图7 空载以及满载条件下无故障轴承的比较结果

3.2 无故障电动机轴承的振动分析

当无轴承故障的三相感应电动机,在空载和满载条件下运行时,间隙中存在均匀磁场。利用快速傅氏变换算法对振动信号进行频谱分析,如图7所示。从图7可看出,基本频率分量占优势,表明电动机的轴承无故障。

3.3 多故障轴承的振动分析

当轴承出现多重故障时,感应电动机在空载条件下运行,转子的径向运动会导致出现混合间隙偏心率。因此,电动机的振动和噪声较多,温度升高,出现咔哒声。MEMS加速计能够捕获电动机振动信号,利用FFT分析仪进行频谱分析。图8是空载条件下多故障轴承与无故障轴承在振动频率方面的比较。

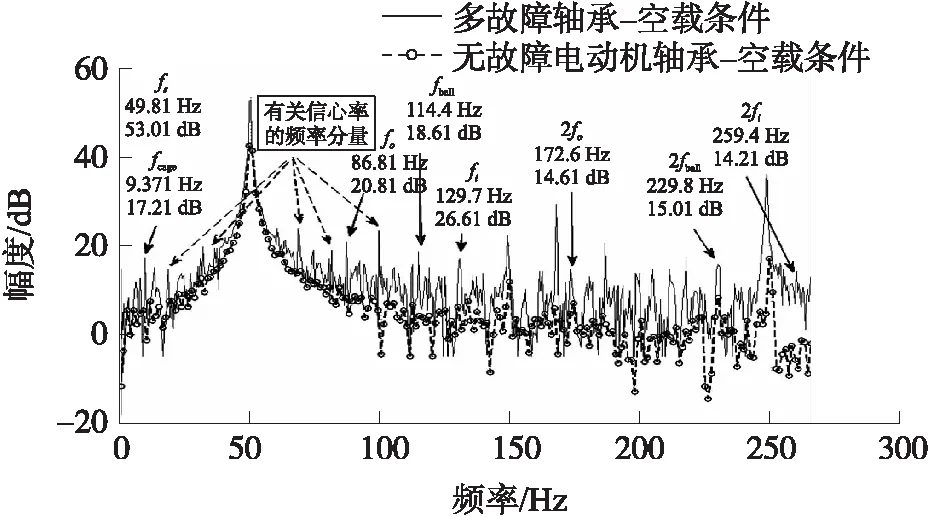
图8 空载条件下多故障轴承与无故障轴承的振动比较

从图8可以看出,离散峰值出现在fcage、fo、fi和fball,表明保持架、内外圈以及滚珠存在故障。从图8也可以看出,采用本方法能够检测轴承多故障以及轴承故障导致的混合间隙偏心率。表2是多故障频率分量以及幅度(dB)。表3是利用提出方法实验得出的故障频率,与根据式(1)～式(4)得出的理论值之间的比较。从表3可看出,结果十分相似。

表2 空载条件下多故障轴承故障频率的实验值

表3 空载条件下实验所得故障频率与理论值的比较

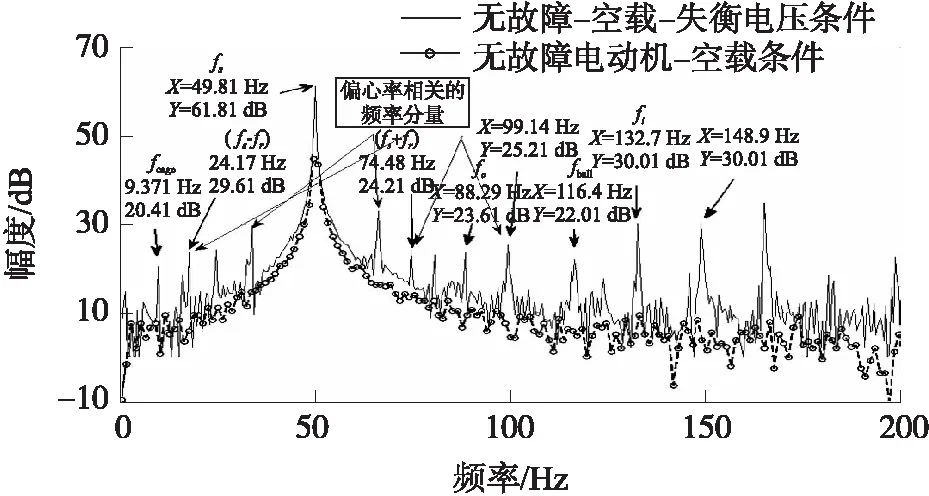
图9 空载以及失衡电压条件下多故障轴承与无故障轴承的振动比较

3.4 失衡电压下轴承多故障的振动分析

电动机在失衡电压条件下运行时,MEMS加速计同样也捕获了振动特征,证实该电动机的轴承存在多重故障。FFT分析仪进行频谱分析之后,可知离散故障频率出现在fcage、fo、fi和fball,如图9所示,表明保持架、内外圈以及滚珠存在缺陷。另外,从图9可看出,失衡电压条件下的故障频率幅度高于平衡电源电压条件下的幅度。表4是故障频率以及幅度。从表4可看出,在失衡电压条件下轴承故障较严重。

表4 空载以及失衡电压条件下多故障轴承故障频率的实验值

图10是空载以及单相条件下多重故障轴承振动频谱与无故障轴承振动频谱的比较。FFT分析仪对单相条件下电动机振动进行分析之后,可知独一无二的峰值出现在fcage、fo、fi和fball,如图10所示,表明保持架、内外圈以及滚珠存在故障。表5是故障频率以及幅度。

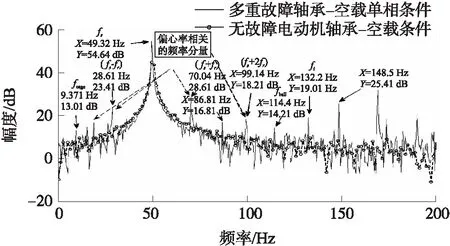
图10 空载以及单相条件下多重故障轴承与无故障轴承的比较

故障分量fcagefofifball频率/Hz9.26186.17132.3114.3幅度/dB13.1116.7719.03142.11

通过比较表2、表4和表5可知,空载以及失衡电压条件下的多故障频率的振幅大于空载以及单相条件下的多故障频率的振幅,而且在空载以及失衡电压条件下,fcage、fo、fi和fball处的多故障轴承故障频率幅度大于平衡电源以及单相条件下的幅度;原因在于,在失衡电压条件下间隙中的磁通密度受到歪曲。另外,显而易见的是,在失衡电压以及单相条件下,相较于其他轴承零件,故障轴承的内圈更易受到影响。

图11和图12是多故障轴承与内外圈出现单点缺陷轴承的比较。从图11可看出,内圈出现单点缺陷轴承的振动频谱仅仅包含BPFI,无其他故障频率;而多故障轴承的振动频谱包含全部(4个)故障频率。同样,在图12中,BPFO处的主要峰值表示外圈存在单点缺陷,而多重频率表示多重故障。

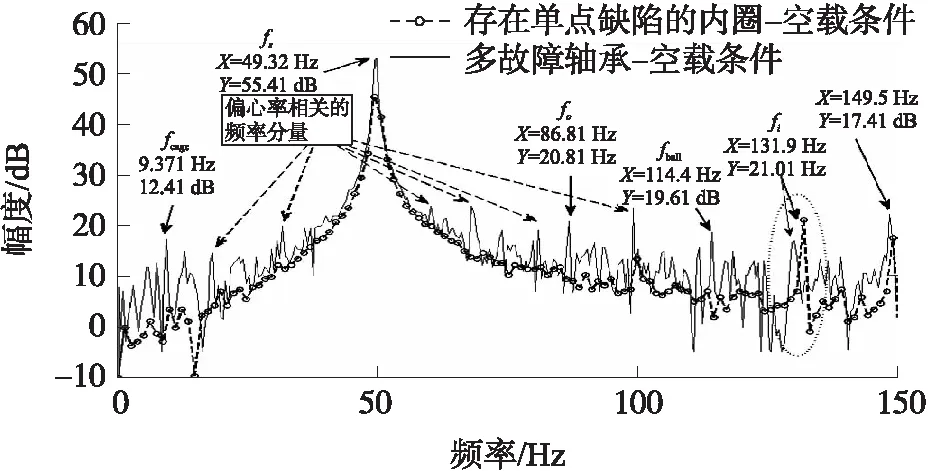
图11 多故障轴承与内圈缺陷轴承的振动比较

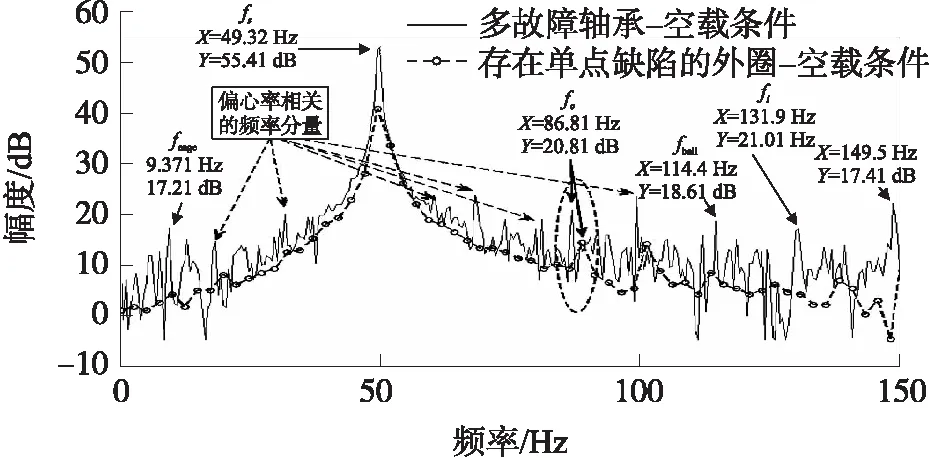
图12 多故障轴承与外圈缺陷轴承的振动比较

根据式(9)可知,除了故障特征频率,因轴承存在多故障引起的振动会导致产生与混合间隙偏心率相关的频率分量,。从实验结果中可发现,图8～图12明确显示了因轴承存在多故障引起的间隙调制的影响。大约50 Hz时出现边带频率分量(fs±fr)、(fs±fr/2)和(fs±fr/3),同时大约150 Hz时出现边带频率分量(3fs±fr/2)和(3fs±fr/3),表明存在动态偏心率;鉴于大约100 Hz时出现边带频率分量(fs+2fr),表明存在静态偏心率。因此,如果存在轴承多故障,测试下的电动机也会同时存在混合间隙偏心率。

4 结论

本文提出了一种利用MEMS加速计进行了振动分,从而实现电动机深沟球轴承多重故障检测的方法,同时分析了轴承多故障对间隙偏心率的影响。在振动频谱中,fcage、fo、fi和fball处出现故障特征频率,表明轴承存在多重故障。在空载条件下,振动特征分析可以提取出较明显的故障峰值,用于识别多故障。大约50 Hz、150 Hz和100 Hz处出现边带频率分量,表明电动机内存在因轴承故障引起的混合间隙偏心率。实验结果显示,失衡电压条件下的轴承故障频率幅度大于单相条件下的幅度。实验结果表明,利用MEMS加速计进行振动分析的方法,能够在低成本的条件下,有效检测并识别出三相感应电动机存在的复杂轴承故障。

[1] 杨正友,彭涛. 基于振动信号分析和支持向量机的滚动轴承故障诊断[J]. 湖南工业大学学报,2009,23(1):96-99.

[2] 李辉,郑海起,唐力伟. 基于改进双树复小波变换的轴承多故障诊断[J]. 振动、测试与诊断,2013,33(1):53-59.

[3] 傅勤毅,王峰林,李明章,等. 滚动轴承故障诊断中的多参数综合判别方法[J]. 哈尔滨工业大学学报,1997(3):57-60.

[4] Frosini L,HarliCa C,Szabó L. Induction Machine Bearing Fault Detection by Means of Statistical Processing of the Stray Flux Measurement[J]. IEEE Transactions on Industrial Electronics,2015,62(3):1846-1854.

[5] Leite V C M N,Borges d S J G,Veloso G F C,et al. Detection of Localized Bearing Faults in Induction Machines by Spectral Kurtosis and Envelope Analysis of Stator Current[J]. IEEE Transactions on Industrial Electronics,2015,62(3):1-1.

[6] Önel I Y,Benbouzid M E H. Induction Motors Bearing Failures Detection and Diagnosis:Park and Concordia Transform Approaches Comparative Study[J]. IEEE/ASME Transactions on Mechatronics,2008,13(2):257-262.

[7] Zarei J,Poshtan J. An Advanced Park’s Vectors Approach for Bearing Fault Detection[C]//IEEE International Conference on Industrial Technology. IEEE,2006:213-219.

[8] Cong F,Chen J,Dong G,et al. Vibration Model of Rolling Element Bearings in a Rotor-Bearing System for Fault Diagnosis[J]. Journal of Sound and Vibration,2013,332(8):2081-2097.

[9] 张淑清,陈白,张立国. 小波分析算法研究及在齿轮与滚动轴承故障诊断中应用[J]. 传感技术学报,2007,20(5):1196-1198.

[10] Konar P,Chattopadhyay P. Bearing Fault Detection of Induction Motor Using Wavelet and Support Vector Machines(SVMs)[J]. Applied Soft Computing,2011,11(6):4203-4211.

BearingFaultDetectionBasedonMEMSAccelerationSensor*

ZHANGYi*

(Department of Electronic Information and Physics Changzhi University,Changzhi Shanxi 046011,China)

A vibration analysis by using MEMS acceleration sensor with low cost,simple method is proposed for the detection of multiple faults of motor of deep groove ball bearing. The bearing fault characteristic frequency is first analyzed. Then by means of the fast Fourier transform algorithm on bearing appears fault of motor vibration frequency were analyzed. From the vibration spectrum extraction of fault frequency to diagnose multiple faults in bearings. At the same time,the fundamental frequency component around the sideband frequency components shows that the fault exists in the bearing air gaps. Under no load,the single-phase voltage unbalance conditions through experiments on the proposed method had been studied. The results show that the extracted fault frequency and theoretical value both are very close to,which show that the proposed method can effectively detect and identify the multi fault characteristic of the induction motor.

FFT;MEMS accelerometer;fault detection;vibration characteristic analysis

10.3969/j.issn.1005-9490.2017.06.042

项目来源:长治学院科研课题项目(2013203)

2016-05-16修改日期2016-07-06

TP273

A

1005-9490(2017)06-1550-06

张毅(1983-),男,汉族,山西长治人,硕士,讲师,研究方向为信号分析与处理、振动分析,zhangyi1983cz@sina.com。