一种网格多涡卷混沌Colpitts振荡器及其电路实现*

王振宇,苏咏梅

(郑州职业技术学院电气电子工程系,郑州 450121)

一种网格多涡卷混沌Colpitts振荡器及其电路实现*

王振宇,苏咏梅*

(郑州职业技术学院电气电子工程系,郑州 450121)

基于单涡卷混沌Colpitts振荡器模型,对使用不同非线性函数构造多涡卷混沌Copitts振荡器模型进行了研究,并提出了一种网格多涡卷混沌Colpitts振荡器模型。利用阶跃函数代替单涡卷混沌Colpitts振荡器模型中的非线性函数,以及增加一个饱和函数,构造了一个能产生网格多涡卷混沌吸引子的Colpitts振荡器模型。通过数值仿真与电路实验,验证了该网格多涡卷混沌Colpitts振荡器的可行性。

混沌;Colpitts振荡器;电路实现;网格多涡卷混沌吸引子

多涡卷混沌吸引子较单涡卷混沌吸引子,其结构和动力学行为更复杂,因此对多涡卷混沌吸引子[1-12]的研究受到了人们广泛的关注。对于多涡卷的构造,其基本方法是设计合适的非线性函数,通过非线性函数控制多涡卷混沌系统产生不同方向和不同数量的多涡卷混沌吸引子。文献[1-3]在蔡氏电路的基础上,通过增加不同的非线性函数构造了一维多涡卷混沌吸引子,文献[4]在Jerk模型上,引入了一个三角函数,构造了一维多涡卷混沌吸引子;文献[5-6]在蔡氏电路上,分别引入了时滞和阶跃函数,以及锯齿波和阶跃函数,构造了二维网格多涡卷混沌吸引子;文献[7-8]对Colpitts模型进行了研究,通过设计两个相同的分段三角波函数,构造了二维网格多涡卷混沌吸引子;文献[9-10]构造了动力学行为更为复杂的多方向多涡卷混沌吸引子。虽然已有大量的文献报道了对多涡卷混沌吸引子研究,但这些多涡卷混沌吸引子大多数是基于蔡氏电路构造的,而对于在单涡卷混沌Colpitts振荡器模型的基础上,构造多涡卷混沌吸引子的研究还较少。而且文献[7-8]构造的二维网格多涡卷混沌吸引子使用的是两个相同的分段三角波函数,因此,研究使用不同的非线性函数构造多涡卷混沌Copitts振荡器模型具有意义。

本文在单涡卷混沌Copitts振荡器模型的基础上,通过引入阶跃函数和饱和函数,构造了一个能产生网格多涡卷混沌吸引子的Copitts振荡器模型。通过数值仿真,获得的2×2、3×3、4×4、5×5涡卷混沌吸引子。在构造的网格多涡卷混沌Copitts振荡器模型的基础上,设计了相应的硬件电路。通过电路实验,验证了该网格多涡卷混沌Copitts振荡器模型的可行性。

1 单涡卷混沌Colpitts振荡器模型

Colpitts振荡器经归一化处理后的无量纲状态方程如下[12]:

(1)

图2 系统(3)产生的网格多涡卷混沌吸引子

式中:g,Q,k为系统参数,f(y)为系统的非线性函数。

f(y)=e-y-1

(2)

取g=3.1623,Q=1.4158,k=0.5,系统(1)能产生单涡卷混沌吸引子,如图1所示。

图1 单涡卷混沌吸引子

2 网格多涡卷混沌Colpitts振荡器模型

在系统(1)中,令k=0.5,a=2g/Q,b=Qk(1-k)/g,c=1/Q,并用非线性函数[Bh(y)-By]代替f(y),同时在系统(1)的第3个方程中加入一个非线性函数g(x),从而构造了一个新的Colpitts振荡器模型,其无量纲状态方程为

(3)

式中:h(y)为阶跃函数,g(x)为饱和函数,其表达式如下

(4)

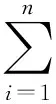
(5)

式(4)和式(5)中,A∈(0,1),N,M∈{0,1,2,…},m=[m1,m2,…,mn-1,mn]=[1.5,-1.5,…,-1.5,1.5,e],E=[E1,E2,…,EN]=[1,3,5,…,2n-1],当n为偶数时,e=-0.5,当n为奇数时,e=0.5。令a=1,b=0.5,c=0.7,A=0.5,B=2.5,系统(3)能产生(N+M+2)×n涡卷混沌吸引子。

取N=M=0,n=2,系统(3)产生的2×2涡卷混沌吸引子如图2(a)所示;取N=1,M=0,n=3,系统(3)产生的3×3涡卷混沌吸引子如图2(b)所示;取N=M=1,n=4,系统(3)产生的4×4涡卷混沌吸引子如图2(c)所示;取N=2,M=1,n=5,系统(3)产生的5×5涡卷混沌吸引子如图2(d)所示。

3 网格多涡卷混沌Colpitts振荡器的电路设计

根据系统(3)设计的网格多涡卷混沌Colpitts振荡器的电路图如图3所示。

取N=2,M=1,n=5,设计阶跃函数(4)的电路图如图4所示,饱和函数(5)的电路图如图5所示。

图3 网格多涡卷混沌Colpitts振荡器的电路图

图4 阶跃函数电路图

图5 饱和函数电路图

在图3～图5中,使用的运算放大器的型号为UA741CN,其电源电压E=±15 V,输出饱和值Vsat≈±13.5 V。乘法器的型号为AD633JN,其增益为0.1。E+和E-分别接电源电压E的正极和负极,即E+=15 V,E-=-15 V。电阻R=10 kΩ,R0=10 kΩ,R1=1 kΩ,R2=1 kΩ,R3=1 kΩ,R4=10 kΩ,R5=4 kΩ,R6=4 kΩ,R7=10 kΩ,R8=20 kΩ,R9=20 kΩ,R10=14.3 kΩ,R11=10 kΩ,RVI=13.5 kΩ,RE=29 kΩ,RE1=1 kΩ,RE2=3 kΩ,RE3=5 kΩ,Rm1=45 kΩ,Rm3=27 kΩ,Rm2为可调电阻。电容C0=10 nF。

图6 电路实验结果

4 电路实验结果

根据图3～图5,搭建了实际硬件电路。当开关k3置1,k2置2,k1、k5、k6闭合时,调节电阻Rm2=45 kΩ,在示波器上可获得2×2涡卷混沌吸引子,如图6(a)所示;当开关k3置2,k2置1,k1、k5、k6、k7闭合时,调节电阻Rm2=15 kΩ,在示波器上可获得2×3涡卷混沌吸引子,如图6(b)所示;当开关k3置2,k2置1,k1、k2、k5、k6、k7闭合时,调节电阻Rm2=15 kΩ,在示波器上可获得3×3涡卷混沌吸引子,如图6(c)所示。

比较图2和图6可知,电路实验结果验证了数值仿真结果,表明该网格多涡卷混沌Colpitts振荡器模型的可行性。

5 结论

本文提出了一种网格多涡卷混沌Colpitts振荡器模型。通过数值仿真分析,该网格多涡卷混沌Colpitts振荡器模型能产生(N+M+2)×n涡卷混沌吸引子,并给出了产生2×2、3×3、4×4、5×5涡卷混沌吸引子的数值仿真结果。最后,设计了该网格多涡卷混沌Colpitts振荡器模型的电路。通过硬件电路实验,在示波器上获得了2×2、2×3、3×3涡卷混沌吸引子,验证了数值仿真结果。

由于本文使用了不同的非线性函数来构造网格多涡卷混沌Colpitts振荡器模型,因此,进一步补充和完善了现有的多涡卷混沌Colpitts振荡器模型;同时,在保密通信工程上,也为掩蔽信息提供了更多的选择。

[1] 孙克辉,艾星星,左婷,等. 多涡卷Chua混沌吸引子的设计与性能分析[J]. 动力学与控制学报,2015,13(1):11-17.

[2] 马英杰,李彦兵,杨亚涛. 变形蔡氏混沌系统及其电路实现[J]. 北京邮电大学学报,2015,38(1):36-39.

[3] Ma Y,Li Y,Jiang X. Simulation and Circuit Implementation of 12-Scroll Chaotic System[J]. Chaos,Solitons and Fractals,2015,75(6):127-133.

[4] 俞清,姜盼,陆菱,等. 基于Jerk形式的多涡卷混沌电路[J]. 常州大学学报(自然科学版),2016,28(2):83-87.

[5] 张朝霞,禹思敏. 用时滞和阶跃序列组合生成网格多涡卷蔡氏混沌吸引子[J]. 物理学报,2009,58(1):120-130.

[6] Yu S,Tang W K S,Chen G. Generation of n×m-Scroll Attractors Under a Chua-Circuit Framework[J]. Int J Bifurcation of Chaos,2007,17(11):3951-3964.

[7] 包伯成,刘中,许建平,等. 基于Colpitts振荡器模型生成的多涡卷超混沌吸引子[J]. 物理学报,2010,59(3):1540-1548.

[8] Yu F,Wang C,He H. Grid Multiscroll Hyperchaotic Attractors Based on Colpitts Oscillator Mode with Controllable Grid Gradient and Scroll Numbers[J]. Journal of Applied Research and Technology,2013,11(3):371-380.

[9] Lü J,Yu S,Leung H,Chen G. Experimental Verification of Multidirectional Multiscroll Chaotic Attractors[J]. IEEE Trans Circuits Syst I,Reg. Papers,2006,53(1):149-165.

[10] Wang C,Luo X,Wan Z. Generation and Circuit Implementation of Multi-Block Multidirectional Grid Multi-Scroll Chaotic Attractors[J]. Optik-International Journal for Light and Electron Optics,2014 125(22):6716-6721.

[11] Chen L,Pan W,Wu R,et al. Generation and Circuit Implementation of Fractional-Order Multi-Scroll Attractors[J]. Chaos,Solitons and Fractals,2016,85(4):22-31.

[12] Maggio G M,Feo O D,Kennedy M P. Nonlinear Analysis of the Colpitts Oscillator and Applications to Design[J]. IEEE Trans Circuits Syst I,Fundam Theory Appl,1999,46(9):1118-1130.

AGridMulti-ScrollChaoticAttractorandItsCircuitImplementationBasedonColpittsOscillatorModel*

WANGZhenyu,SUYongmei*

(Department of Electrical and Electronic Engineering,Zhengzhou Technical College,Zhengzhou 450121,China)

Based on the spiral chaotic Colpitts oscillator model,it is studied to construct multi-scroll chaotic Copitts oscillator model via different nonlinear functions,and a grid multi-scroll chaotic Colpitts oscillator model is presented. Through replacing the nonlinear function of the spiral chaotic Colpitts oscillator model with a step function,and introducing a saturation function,a new Colpitts oscillator model is constructed,which is able to generate grid multi-scroll chaotic attractors. Through numerical simulation and circuit experiment,the feasibility of the grid multi-scroll chaotic Colpitts oscillator model is verified.

chaos;Clopitts oscillator model;circuit implementation;grid multi-scroll chaotic attractors

10.3969/j.issn.1005-9490.2017.06.022

项目来源:2016年度河南省高等学校重点科研项目应用研究计划(16B413007)

2016-10-18修改日期2017-01-14

O415.5

A

1005-9490(2017)06-1441-04

王振宇(1972-),男,汉族,,河南郑州人,本科,郑州职业技术学院副教授,研究方向为电气控制应用,wangzhenyu 22222@21cn.com;

苏咏梅(1971-),女,汉族,河南郑州人,硕士,郑州职业技术学院副教授,研究方向为电子技术与电气控制系统,15038310680@163.com。